第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
11. (2024·扬州期中)如图,在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB交AB于点F,EG⊥AC交AC的延长线于点G.
(1)连接BE,CE,求证:BF=CG;
(2)若AB=10,AC=6,求AF的长;
(3)在(2)的条件下,△ABC中连接AD,直接写出AD的取值范围;
(4)在(2)的条件下,若AE与BC相交于H,当BC=12时,直接写出BH的值.
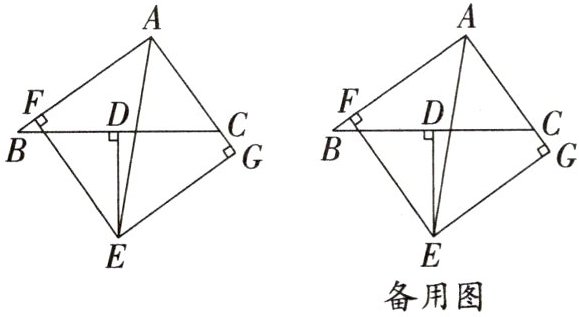
(1)连接BE,CE,求证:BF=CG;
(2)若AB=10,AC=6,求AF的长;
(3)在(2)的条件下,△ABC中连接AD,直接写出AD的取值范围;
(4)在(2)的条件下,若AE与BC相交于H,当BC=12时,直接写出BH的值.

答案:
11.
(1)如图①,
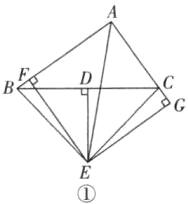
∵ED⊥BC,D为BC的中点,
∴BE = EC。
∵EF⊥AB,EG⊥AC,AE是∠BAC的平分线,
∴EF = EG,∠EFB = ∠EGC = 90°。在Rt△BEF和Rt△CEG中,$\begin{cases}BE = EC, \\ EF = EG,\end{cases}$
∴Rt△BEF ≌ Rt△CEG(HL),
∴BF = CG。
(2)
∵EF⊥AB,EG⊥AC,
∴∠AFE = ∠AGE = 90°。在Rt△AFE和Rt△AGE中,$\begin{cases}AE = AE, \\ EF = EG,\end{cases}$
∴Rt△AFE ≌ Rt△AGE(HL),
∴AF = AG。
∵BF = CG,
∴AF + AG = AB + AC。
∵AF = AG,
∴AF = $\frac{1}{2} \times (AF + AG) = \frac{1}{2} \times (AB + AC) = \frac{1}{2} \times (10 + 6) = 8$。
(3) 2 < AD < 8. 解析:如图②,延长AD到P,使AD = DP,连接BP,
∵BD = CD,∠ADC = ∠PDB,
∴△ADC ≌ △PDB(SAS),
∴BP = AC = 6,AD = PD,
∴10 - 6 < AP < 10 + 6,即4 < 2AD < 16,
∴2 < AD < 8。


(4) BH的值为$\frac{15}{2}$ 解析:如图③,过点A作AM⊥BC于M,设CM = x,则BM = 12 - x。由勾股定理得$AM^2 = AC^2 - CM^2 = AB^2 - BM^2$,
∴$6^2 - x^2 = 10^2 - (12 - x)^2$,
∴$x = \frac{10}{3}$,
∴$CM = \frac{10}{3}$,
∴$AM = \sqrt{6^2 - (\frac{10}{3})^2} = \sqrt{36 - \frac{100}{9}} = \frac{4\sqrt{14}}{3}$。过点H作HJ⊥AB于J,作HQ⊥AC于Q,
∵AH平分∠BAC,
∴HJ = HQ,
∴$\frac{1}{2} \times \frac{4\sqrt{14}}{3} \times 12 = \frac{1}{2} \times 10HJ + \frac{1}{2} \times 6HJ$,
∴$HJ = \sqrt{14}$,
∴$\frac{1}{2} \times BH \times \frac{4\sqrt{14}}{3} = \frac{1}{2} \times 10 \times \sqrt{14}$,
∴$BH = \frac{15}{2}$。
11.
(1)如图①,

∵ED⊥BC,D为BC的中点,
∴BE = EC。
∵EF⊥AB,EG⊥AC,AE是∠BAC的平分线,
∴EF = EG,∠EFB = ∠EGC = 90°。在Rt△BEF和Rt△CEG中,$\begin{cases}BE = EC, \\ EF = EG,\end{cases}$
∴Rt△BEF ≌ Rt△CEG(HL),
∴BF = CG。
(2)
∵EF⊥AB,EG⊥AC,
∴∠AFE = ∠AGE = 90°。在Rt△AFE和Rt△AGE中,$\begin{cases}AE = AE, \\ EF = EG,\end{cases}$
∴Rt△AFE ≌ Rt△AGE(HL),
∴AF = AG。
∵BF = CG,
∴AF + AG = AB + AC。
∵AF = AG,
∴AF = $\frac{1}{2} \times (AF + AG) = \frac{1}{2} \times (AB + AC) = \frac{1}{2} \times (10 + 6) = 8$。
(3) 2 < AD < 8. 解析:如图②,延长AD到P,使AD = DP,连接BP,
∵BD = CD,∠ADC = ∠PDB,
∴△ADC ≌ △PDB(SAS),
∴BP = AC = 6,AD = PD,
∴10 - 6 < AP < 10 + 6,即4 < 2AD < 16,
∴2 < AD < 8。


(4) BH的值为$\frac{15}{2}$ 解析:如图③,过点A作AM⊥BC于M,设CM = x,则BM = 12 - x。由勾股定理得$AM^2 = AC^2 - CM^2 = AB^2 - BM^2$,
∴$6^2 - x^2 = 10^2 - (12 - x)^2$,
∴$x = \frac{10}{3}$,
∴$CM = \frac{10}{3}$,
∴$AM = \sqrt{6^2 - (\frac{10}{3})^2} = \sqrt{36 - \frac{100}{9}} = \frac{4\sqrt{14}}{3}$。过点H作HJ⊥AB于J,作HQ⊥AC于Q,
∵AH平分∠BAC,
∴HJ = HQ,
∴$\frac{1}{2} \times \frac{4\sqrt{14}}{3} \times 12 = \frac{1}{2} \times 10HJ + \frac{1}{2} \times 6HJ$,
∴$HJ = \sqrt{14}$,
∴$\frac{1}{2} \times BH \times \frac{4\sqrt{14}}{3} = \frac{1}{2} \times 10 \times \sqrt{14}$,
∴$BH = \frac{15}{2}$。
12. (2024·武威期中)如图,在三角形ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,点G是AD上的一点,且∠ACG=45°,连接BG交CE于P,连接DP,下列结论:①AC=AE,②CD=BE,③BG+2DP=AD,④PG=PE,其中正确的有( )

A. ①②③
B. ①②④
C. ①③④
D. ①②③④

A. ①②③
B. ①②④
C. ①③④
D. ①②③④
答案:
12.B 解析:如图,设CE与AD交于点O,
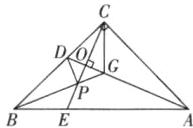
∵∠ACB = 90°,AC = BC,
∴∠ABC = ∠BAC = 45°。
∵AD平分∠BAC,
∴∠CAD = ∠BAD = 22.5°。
∵CE⊥AD,
∴∠AOC = ∠AOE = 90°,
∴∠ACO = ∠AEO = 67.5°,
∴AC = AE,故①正确;
∵∠ACB = 90°,
∴∠BCE = ∠CAG = 22.5°,在△ACG和△CBE中,$\begin{cases}∠BCE = ∠CAG, \\ BC = AC, \\ ∠CBE = ∠ACG,\end{cases}$
∴△ACG ≌ △CBE(ASA),
∴CG = BE。
∵∠ACB = 90°,
∴∠ADC = 67.5°。
∵∠CGD = ∠CAD + ∠ACG = 22.5° + 45° = 67.5°,
∴∠ADC = ∠CGD = 67.5°,
∴CD = CG,
∴CD = BE,故②正确;
∵CE⊥AD,
∴DO = GO,
∴CE垂直平分DG,
∴DP = PG。
∵∠ACG = ∠BCG = 45°,
∴CG所在直线垂直平分AB,
∴BG = AG,
∴AD = AG + DG = BG + DG,DG ≠ 2DP,故③错误;
∵BG = AG,
∴∠GAB = ∠GBA = ∠PCG = 22.5°,由上可知CD = CG,CD = BE,
∴CG = BE。在△PBE和△PCG中,$\begin{cases}∠PBE = ∠PCG, \\ ∠BPE = ∠CPG, \\ BE = CG,\end{cases}$
∴△PBE ≌ △PCG(AAS),
∴PG = PE,故④正确。综上,①②④正确。
12.B 解析:如图,设CE与AD交于点O,

∵∠ACB = 90°,AC = BC,
∴∠ABC = ∠BAC = 45°。
∵AD平分∠BAC,
∴∠CAD = ∠BAD = 22.5°。
∵CE⊥AD,
∴∠AOC = ∠AOE = 90°,
∴∠ACO = ∠AEO = 67.5°,
∴AC = AE,故①正确;
∵∠ACB = 90°,
∴∠BCE = ∠CAG = 22.5°,在△ACG和△CBE中,$\begin{cases}∠BCE = ∠CAG, \\ BC = AC, \\ ∠CBE = ∠ACG,\end{cases}$
∴△ACG ≌ △CBE(ASA),
∴CG = BE。
∵∠ACB = 90°,
∴∠ADC = 67.5°。
∵∠CGD = ∠CAD + ∠ACG = 22.5° + 45° = 67.5°,
∴∠ADC = ∠CGD = 67.5°,
∴CD = CG,
∴CD = BE,故②正确;
∵CE⊥AD,
∴DO = GO,
∴CE垂直平分DG,
∴DP = PG。
∵∠ACG = ∠BCG = 45°,
∴CG所在直线垂直平分AB,
∴BG = AG,
∴AD = AG + DG = BG + DG,DG ≠ 2DP,故③错误;
∵BG = AG,
∴∠GAB = ∠GBA = ∠PCG = 22.5°,由上可知CD = CG,CD = BE,
∴CG = BE。在△PBE和△PCG中,$\begin{cases}∠PBE = ∠PCG, \\ ∠BPE = ∠CPG, \\ BE = CG,\end{cases}$
∴△PBE ≌ △PCG(AAS),
∴PG = PE,故④正确。综上,①②④正确。
13. (2024·大连期中)如图,已知在△ABC中,点G是AB边上一点,点E是BC延长线上一点,GE交AC于点D,点F是AD上一点,连接GF,∠GFC=2∠BAC,∠FGE=2∠BEG,AC=GE,GH⊥BC于点H.
(1)写出与∠BAC相等的角,∠BAC=______;
(2)若∠GFC=∠FGE,在图中找出与AG相等的线段并证明;
(3)若HC=2,CE=3,求BC的长度.

(1)写出与∠BAC相等的角,∠BAC=______;
(2)若∠GFC=∠FGE,在图中找出与AG相等的线段并证明;
(3)若HC=2,CE=3,求BC的长度.

答案:
13.
(1)∠AGF
(2)AG = CE. 证明:
∵∠GFC = 2∠BAC,∠GFC = ∠FGE,∠FGE = 2∠BEG,
∴∠BAC = ∠BEG。在△BAC和△BEG中,$\begin{cases}∠B = ∠B, \\ ∠BAC = ∠BEG, \\ AC = EG,\end{cases}$
∴△BAC ≌ △BEG(AAS),
∴BC = BG,AB = EB,
∴AB - BG = EB - BC,即AG = CE。
(3)如图,延长FG交CB的延长线于点M,过点M作MN//AC交AB的延长线于点N,∠MGN = ∠AGF = ∠BAC,则∠N = ∠BAC,
∴∠N = ∠MGN,
∴MG = MN。
∵∠FGE = 2∠BEG = ∠BEG + ∠GME,
∴∠BEG = ∠GME,
∴MG = GE。
∵AC = GE,
∴MN = AC。在△NBM和△ABC中,$\begin{cases}∠NBM = ∠ABC, \\ ∠N = ∠BAC, \\ MN = CA,\end{cases}$
∴△NBM ≌ △ABC(AAS),
∴BM = BC。设BH = x,
∵HC = 2,CE = 3,
∴BM = BC = x + 2,EH = 5。
∴MH = BM + BH = 2x + 2。
∵MG = GE,GH⊥BC,
∴MH = EH。
∴2x + 2 = 5,解得$x = \frac{3}{2}$,
∴$BH = \frac{3}{2}$,
∴$BC = BH + HC = \frac{3}{2} + 2 = \frac{7}{2}$,故BC的长度为$\frac{7}{2}$。

13.
(1)∠AGF
(2)AG = CE. 证明:
∵∠GFC = 2∠BAC,∠GFC = ∠FGE,∠FGE = 2∠BEG,
∴∠BAC = ∠BEG。在△BAC和△BEG中,$\begin{cases}∠B = ∠B, \\ ∠BAC = ∠BEG, \\ AC = EG,\end{cases}$
∴△BAC ≌ △BEG(AAS),
∴BC = BG,AB = EB,
∴AB - BG = EB - BC,即AG = CE。
(3)如图,延长FG交CB的延长线于点M,过点M作MN//AC交AB的延长线于点N,∠MGN = ∠AGF = ∠BAC,则∠N = ∠BAC,
∴∠N = ∠MGN,
∴MG = MN。
∵∠FGE = 2∠BEG = ∠BEG + ∠GME,
∴∠BEG = ∠GME,
∴MG = GE。
∵AC = GE,
∴MN = AC。在△NBM和△ABC中,$\begin{cases}∠NBM = ∠ABC, \\ ∠N = ∠BAC, \\ MN = CA,\end{cases}$
∴△NBM ≌ △ABC(AAS),
∴BM = BC。设BH = x,
∵HC = 2,CE = 3,
∴BM = BC = x + 2,EH = 5。
∴MH = BM + BH = 2x + 2。
∵MG = GE,GH⊥BC,
∴MH = EH。
∴2x + 2 = 5,解得$x = \frac{3}{2}$,
∴$BH = \frac{3}{2}$,
∴$BC = BH + HC = \frac{3}{2} + 2 = \frac{7}{2}$,故BC的长度为$\frac{7}{2}$。

14. (2024·兰州期中)【问题提出】
(1)如图①,在△ABC中,∠B=∠ACB,点D是AB上一点,DE//AC交BC于点E,点F是CE的中点,连接DF并延长交AC的延长线于点G,求证:BD=CG.
【问题探究】
(2)如图②,在四边形ABCD中,AB//CD,点E是BC的中点,连接AE,∠EAF=∠BAE,AF与DC的延长线交于点F.探究线段AB与AF,CF之间的数量关系,并说明理由.
【问题解决】
(3)如图③,某校有一块四边形空地ABCD,现将这块空地规划为实践活动区域,在BC的中点E处修建入口,沿AE修建一条小路(小路的宽度忽略不计),将这块空地分成两部分,在△ABE内种植蔬菜,在四边形ADCE内种花卉,已知∠BAD=60°,AE恰好平分∠BAD,∠B=180°-$\frac{1}{2}$∠BCD,BC=100m,求CD的长.
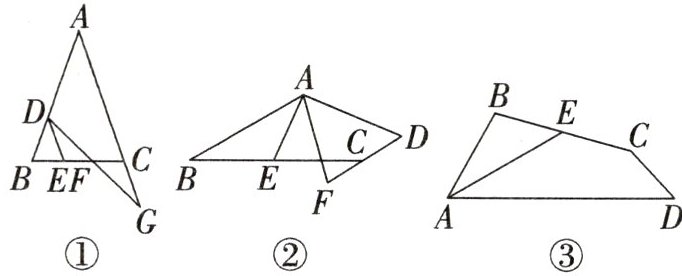
(1)如图①,在△ABC中,∠B=∠ACB,点D是AB上一点,DE//AC交BC于点E,点F是CE的中点,连接DF并延长交AC的延长线于点G,求证:BD=CG.
【问题探究】
(2)如图②,在四边形ABCD中,AB//CD,点E是BC的中点,连接AE,∠EAF=∠BAE,AF与DC的延长线交于点F.探究线段AB与AF,CF之间的数量关系,并说明理由.
【问题解决】
(3)如图③,某校有一块四边形空地ABCD,现将这块空地规划为实践活动区域,在BC的中点E处修建入口,沿AE修建一条小路(小路的宽度忽略不计),将这块空地分成两部分,在△ABE内种植蔬菜,在四边形ADCE内种花卉,已知∠BAD=60°,AE恰好平分∠BAD,∠B=180°-$\frac{1}{2}$∠BCD,BC=100m,求CD的长.

答案:
14.
(1)
∵DE//AG,∠B = ∠ACB,
∴∠FDE = ∠FGC,∠BED = ∠ACB = ∠B,
∴BD = DE。
∵点F是CE的中点,
∴EF = CF。
∵∠FDE = ∠FGC,∠DFE = ∠GFC,EF = CF,
∴△DEF ≌ △GCF(AAS),
∴DE = GC,
∴BD = CG。
(2)AB = AF + CF。理由:分别延长AE,DF,AE与DF的延长线交于点G,如图①。
∵AB//DC,
∴∠B = ∠GCE,∠BAE = ∠EGC。
∵E为BC边的中点,
∴BE = CE,
∴△ABE ≌ △GCE(AAS),
∴AB = CG。又
∵∠EAF = ∠BAE,
∴∠G = ∠EAF,
∴AF = GF,
∴AB = CG = GF + CF = AF + CF。


(3)过C作CM//AB交AE的延长线于点M,延长MC交AD于点N,连接EN,如图②。
∵点E是BC的中点,BC = 100m,
∴BE = CE = 50m。
∵AB//MN,∠BAD = 60°,
∴∠B + ∠ECN = 180°,∠BAD = ∠CND = 60°,∠BAE = ∠M。
∵∠BAE = ∠M,∠AEB = ∠MEC,BE = CE,
∴△ABE ≌ △MCE(AAS),
∴AE = ME。
∵AE平分∠BAD,
∴∠M = ∠BAE = ∠DAE,
∴AN = MN。又AE = ME,
∴NE平分∠ANM,
∴∠ANE = ∠MNE = ∠CND = 60°。
∵∠B = 180° - $\frac{1}{2}$∠BCD,∠B + ∠ECN = 180°,
∴∠ECN = ∠DCN。
∵∠CNE = ∠CND,CN = CN,∠ECN = ∠DCN,
∴△CNE ≌ △CND(ASA),
∴CD = CE = 50m。
14.
(1)
∵DE//AG,∠B = ∠ACB,
∴∠FDE = ∠FGC,∠BED = ∠ACB = ∠B,
∴BD = DE。
∵点F是CE的中点,
∴EF = CF。
∵∠FDE = ∠FGC,∠DFE = ∠GFC,EF = CF,
∴△DEF ≌ △GCF(AAS),
∴DE = GC,
∴BD = CG。
(2)AB = AF + CF。理由:分别延长AE,DF,AE与DF的延长线交于点G,如图①。
∵AB//DC,
∴∠B = ∠GCE,∠BAE = ∠EGC。
∵E为BC边的中点,
∴BE = CE,
∴△ABE ≌ △GCE(AAS),
∴AB = CG。又
∵∠EAF = ∠BAE,
∴∠G = ∠EAF,
∴AF = GF,
∴AB = CG = GF + CF = AF + CF。


(3)过C作CM//AB交AE的延长线于点M,延长MC交AD于点N,连接EN,如图②。
∵点E是BC的中点,BC = 100m,
∴BE = CE = 50m。
∵AB//MN,∠BAD = 60°,
∴∠B + ∠ECN = 180°,∠BAD = ∠CND = 60°,∠BAE = ∠M。
∵∠BAE = ∠M,∠AEB = ∠MEC,BE = CE,
∴△ABE ≌ △MCE(AAS),
∴AE = ME。
∵AE平分∠BAD,
∴∠M = ∠BAE = ∠DAE,
∴AN = MN。又AE = ME,
∴NE平分∠ANM,
∴∠ANE = ∠MNE = ∠CND = 60°。
∵∠B = 180° - $\frac{1}{2}$∠BCD,∠B + ∠ECN = 180°,
∴∠ECN = ∠DCN。
∵∠CNE = ∠CND,CN = CN,∠ECN = ∠DCN,
∴△CNE ≌ △CND(ASA),
∴CD = CE = 50m。
查看更多完整答案,请扫码查看


