第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
1. (2024·中卫月考)下列条件中,不能判定$\triangle ABC$是等腰三角形的是 (
A. $∠A:∠B:∠C=1:1:3$
B. $BC:AC:AB=2:2:3$
C. $∠B=50^{\circ },∠C=80^{\circ }$
D. $2∠A=∠B+∠C$
D
)A. $∠A:∠B:∠C=1:1:3$
B. $BC:AC:AB=2:2:3$
C. $∠B=50^{\circ },∠C=80^{\circ }$
D. $2∠A=∠B+∠C$
答案:
D
2. 若一个三角形的外角平分线与这个三角形的一边平行,则这个三角形一定是 (
A. 锐角三角形
B. 等腰三角形
C. 等边三角形
D. 等腰直角三角形
B
)A. 锐角三角形
B. 等腰三角形
C. 等边三角形
D. 等腰直角三角形
答案:
B
3. (2025·聊城期末)如图,在$\triangle ABC$中,$∠CAB$的平分线AD与$∠CBA$的平分线BD交于点D,过点D作AB的平行线分别交AC,BC于点M,N,若$\triangle ABC$与$\triangle CMN$的周长分别为32,24,则AB的长为 (
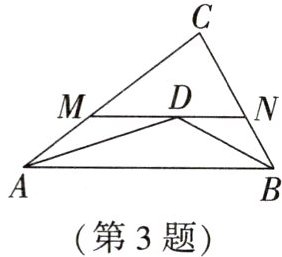
A. 8
B. 15
C. 12
D. 6
A
)
A. 8
B. 15
C. 12
D. 6
答案:
A
4. 将一张长方形纸片按如图所示折叠,若$AB=6cm$,点B到AC距离为4cm,则$S_{\triangle ABC}=$
12
$cm^{2}$.
答案:
12
5. 教材P85习题T9变式 (济宁中考改编)一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西$42^{\circ }$方向上,在海岛B的北偏西$84^{\circ }$方向上.则海岛B到灯塔C的距离是
30
海里.
答案:
30
6. 如图,已知点D为$\triangle ABC$内一点,CD平分$∠ACB,BD⊥CD,∠A=∠ABD$,若$AC=6,BC=4$,则BD的长为______
1
.
答案:
1
7. 如图,在小正方形组成的$4×3$的网格中,点A,B分别在格点上,在图中确定格点C,则以A,B,C为顶点的等腰三角形有
3
个.
答案:
3
8. 如图所示,已知线段a,h,求作以2a为底,底边上的中线为h的等腰三角形.


答案:
如图所示

①作线段AD=a,在AD的延长线上取一点B,使DB=a.②过点D 作AB的垂直平分线MN.③在射线DM上取一点C,使CD=h.④连接AC,BC,则△ABC就是所求作的等腰三角形
如图所示

①作线段AD=a,在AD的延长线上取一点B,使DB=a.②过点D 作AB的垂直平分线MN.③在射线DM上取一点C,使CD=h.④连接AC,BC,则△ABC就是所求作的等腰三角形
9. (2025·泸州期末)如图,在$\triangle ABC$中,$AB=AC,AD⊥BC$于点D,AM是$\triangle ABC$的外角$∠CAE$的平分线.
(1)求证:$AM// BC;$
(2)若DN平分$∠ADC$交AM于点N,证明$\triangle ADN$为等腰直角三角形.
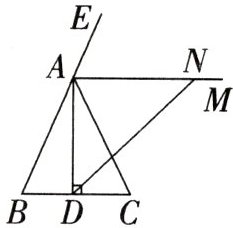
(1)求证:$AM// BC;$
∵AB=AC,AD⊥BC,∴∠BAD=∠CAD=1/2∠BAC;∵AM是△ABC的外角∠CAE的平分线,∴∠EAM=∠MAC=1/2∠EAC,∴∠MAD=∠MAC+∠DAC=1/2∠EAC + 1/2∠BAC=1/2×180°=90°.∵AD⊥BC,∴∠ADC=90°,∴∠MAD+∠ADC=180°,∴AM//BC.
(2)若DN平分$∠ADC$交AM于点N,证明$\triangle ADN$为等腰直角三角形.
由(1)得AM//BC,∴∠AND=∠NDC,∠DAN=∠ADC=90°.∵DN平分∠ADC交AM于点N,∴∠ADN=∠NDC=∠AND=1/2∠ADC=45°,∴△ADN为等腰直角三角形.

答案:
(1)
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=1/2∠BAC;
∵AM是△ABC的外角∠CAE的平分线,
∴∠EAM=∠MAC=1/2∠EAC,
∴∠MAD=∠MAC+∠DAC=1/2∠EAC + 1/2∠BAC=1/2×180°=90°.
∵AD⊥BC,
∴∠ADC=90°,
∴∠MAD+∠ADC=180°,
∴AM//BC.
(2)由
(1)得AM//BC,
∴∠AND=∠NDC,∠DAN=∠ADC=90°.
∵DN平分∠ADC交AM于点N,
∴∠ADN=∠NDC=∠AND=1/2∠ADC=45°,
∴△ADN为等腰直角三角形.
(1)
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=1/2∠BAC;
∵AM是△ABC的外角∠CAE的平分线,
∴∠EAM=∠MAC=1/2∠EAC,
∴∠MAD=∠MAC+∠DAC=1/2∠EAC + 1/2∠BAC=1/2×180°=90°.
∵AD⊥BC,
∴∠ADC=90°,
∴∠MAD+∠ADC=180°,
∴AM//BC.
(2)由
(1)得AM//BC,
∴∠AND=∠NDC,∠DAN=∠ADC=90°.
∵DN平分∠ADC交AM于点N,
∴∠ADN=∠NDC=∠AND=1/2∠ADC=45°,
∴△ADN为等腰直角三角形.
10. (海南中考)已知$\triangle ABC$的三边长分别为4,4,6,在$\triangle ABC$所在平面内画一条直线,将$\triangle ABC$分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 ( )
A. 3条
B. 4条
C. 5条
D. 6条
A. 3条
B. 4条
C. 5条
D. 6条
答案:
B 解析:如图所示,当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形,故选B.

B 解析:如图所示,当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形,故选B.

查看更多完整答案,请扫码查看


