《2025年学霸题中题八年级数学上册人教版》

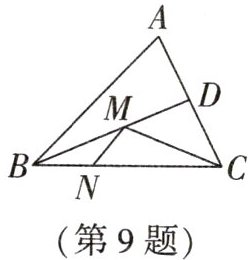
9. 如图,在锐角三角形ABC中,$AB=4,△ABC$的面积为8,BD平分$∠ABC$.若M,N分别是BD,BC上的动点,则$CM+MN$的最小值是 ( )

A. 3
B. 4
C. 5
D. 6

答案：
B 解析：如图，过点C作CE ⊥ AB，垂足为点E，交BD于点M'，过点M'作M'N' ⊥ BC，垂足为点N'。
∵ BD平分∠ABC，
∴ M'N' = M'E，
　　　　　　　　　　　　　　　　　　
∴ CM' + M'N' = CE，
∴ 当点M与点M'重合时，CM + MN的值最小，等于CE的值。
∵ AB = 4，△ABC的面积为8，
∴ $S_{△ABC} = \frac{1}{2}AB \cdot CE = \frac{1}{2} \times 4 \cdot CE = 8$，
∴ CE = 4，
∴ CM + MN的最小值为4。故选B。

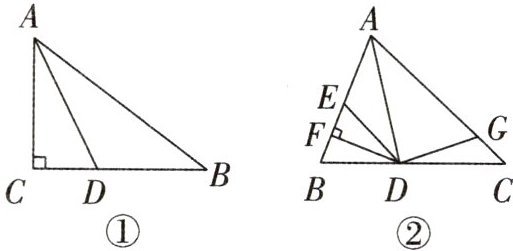
10. (1)(黑龙江中考改编)如图①,在$Rt△ABC$中,$∠C=90^{\circ }$,AD平分$∠CAB,AC=6,BC=8,AB=10,CD=$3.
(2)如图②,AD是$△ABC$的角平分线,$DF⊥AB$于点F,$DE=DG,AG=16,AE=8$,若$S_{△ADG}=64$,则$△DEF$的面积为16.

答案：
(1) 3 解析：过点D作DE ⊥ AB于E，
∵ AD平分∠CAB，
∴ CD = DE，
∴ $S_{△ABC} = S_{△ACD} + S_{△ABD} = \frac{1}{2}AC \cdot CD + \frac{1}{2}AB \cdot DE = \frac{1}{2}AC \cdot BC$，即$\frac{1}{2} \times 6 \cdot CD + \frac{1}{2} \times 10 \cdot CD = \frac{1}{2} \times 6 \times 8$，解得CD = 3。
(2) 16 解析：过点D作DH ⊥ AC于H，
∵ $S_{△ADG} = \frac{1}{2} \times AG \times DH = 64$，
∴ DH = 8。
∵ AD是△ABC的角平分线，DF ⊥ AB，DH ⊥ AC，
∴ DF = DH = 8。在Rt△DEF和Rt△DGH中，$\begin{cases} DE = DG \\ DF = DH \end{cases}$，
∴ Rt△DEF ≌ Rt△DGH(HL)，
∴ EF = HG，同理可证得AF = AH。
∴ EF = AF - AE = AH - AE = AG - HG - AE = 16 - EF - 8，
∴ EF = 4，
∴ $S_{△DEF} = \frac{1}{2} \times EF \times DF = 16$。

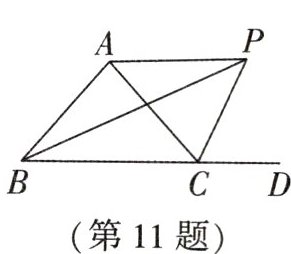
11. 如图,$△ABC$的外角$∠ACD$的平分线CP与内角$∠ABC$的平分线BP交于点P,若$∠BPC=40^{\circ }$,则$∠CAP=$____.

答案：
50° 解析：如图，延长BA，作PN ⊥ BD，PF ⊥ BA，PM ⊥ AC，垂足分别为N，F，M。设∠PCD = x°，
　　　　　　　　　　　　　　　　　　
∵ CP平分∠ACD，
∴ ∠ACP = ∠PCD = x°，PM = PN。
∵ BP平分∠ABC，
∴ ∠ABP = ∠PBC，PF = PN，
∴ PF = PM。
∴ ∠ABP = ∠PBC = ∠PCD - ∠BPC = (x - 40)°，
∴ ∠BAC = ∠ACD - ∠ABC = 2x° - (x° - 40°) - (x° - 40°) = 80°，
∴ ∠CAF = 100°。
∵ $\begin{cases} PA = PA \\ PF = PM \end{cases}$，
∴ Rt△PFA ≌ Rt△PMA(HL)，
∴ ∠FAP = ∠CAP = 50°。

12. 如图,在四边形ABCD中,AO,BO,CO,DO分别是$∠DAB,∠ABC,∠BCD,∠CDA$的平分线.求证:$AB+CD=AD+BC$.


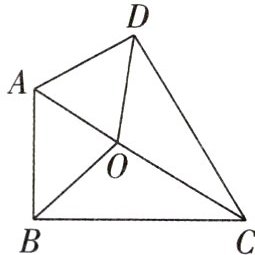
过O分别作OE ⊥ AB，OF ⊥ BC，OG ⊥ CD，OH ⊥ AD，则∠AEO = ∠AHO = 90°。∵ OA平分∠BAD，∴ ∠OAE = ∠OAH。在△OAE和△OAH中，$\begin{cases} ∠OEA = ∠OHA \\ ∠OAE = ∠OAH \\ OA = OA \end{cases}$，∴ △OAE ≌ △OAH(AAS)，∴ AE = AH，同理可得BE = BF，CF = CG，DG = DH，∴ AB + CD = AE + BE + CG + DG，AD + BC = AH + HD + BF + FC，∴ AB + CD = AD + BC。

答案： 过O分别作OE ⊥ AB，OF ⊥ BC，OG ⊥ CD，OH ⊥ AD，则∠AEO = ∠AHO = 90°。
∵ OA平分∠BAD，
∴ ∠OAE = ∠OAH。在△OAE和△OAH中，$\begin{cases} ∠OEA = ∠OHA \\ ∠OAE = ∠OAH \\ OA = OA \end{cases}$，
∴ △OAE ≌ △OAH(AAS)，
∴ AE = AH，同理可得BE = BF，CF = CG，DG = DH，
∴ AB + CD = AE + BE + CG + DG，AD + BC = AH + HD + BF + FC，
∴ AB + CD = AD + BC。

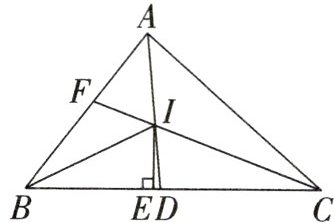
13. 如图所示,I是$△ABC$三内角平分线的交点,$IE⊥BC$于E,AI的延长线交BC于D,CI的延长线交AB于F,下列结论:
①$∠BIE=∠CID$;
②$S_{△ABC}=\frac {1}{2}IE(AB+BC+AC)$;
③$BE=\frac {1}{2}(AB+BC-AC)$;
④$AC=AF+DC$.
其中正确的结论是____①②③.(填序号)

答案： ①②③ 解析：①
∵ I为△ABC三条角平分线的交点，IE ⊥ BC于E，
∴ ∠ABI = ∠IBD。
∵ ∠CID = ∠DAC + ∠ACI = $\frac{1}{2}$(∠BAC + ∠ACB)，∠ABI = $\frac{1}{2}$∠ABC，
∴ ∠CID + ∠ABI = 90°。又
∵ ∠BIE + ∠IBE = 90°，∠ABI = ∠IBE，
∴ ∠BIE = ∠CID，即①正确。②易知点I到△ABC三边的距离相等，
∴ $S_{△ABC} = S_{△ABI} + S_{△BCI} + S_{△ACI} = \frac{1}{2}IE(AB + BC + AC)$，即②正确。③过点I作IH ⊥ AB于H，IG ⊥ AC于G，
∴ IE = IH = IG。
∵ $\begin{cases} AI = AI \\ IH = IG \end{cases}$，
∴ Rt△AHI ≌ Rt△AGI(HL)，
∴ AH = AG，同理，BE = BH，CE = CG，
∴ BE + BH = AB + BC - AH - CE = AB + BC - AC，
∴ $BE = \frac{1}{2}(AB + BC - AC)$，即③正确。④由③得IH = IE。
∵ ∠FHI = ∠DEI = 90°，可得△IHF与△IED不一定全等，
∴ HF不一定等于DE，
∴ AC = AG + CG = AH + CE不一定等于AF + CD，即④错误。故答案为①②③。

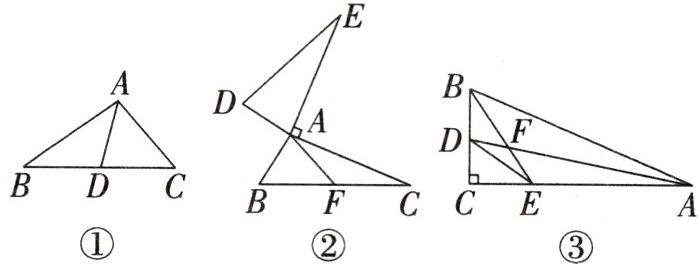
14. (2024·武汉期中)学习理解:
(1)如图①,$AB=6,AC=4$,点D为BC的中点,则AD的取值范围为____.
活学活用:
(2)如图②,$AB=AD,AC=AE,∠BAD=∠CAE=90^{\circ }$,点F为BC的中点. 求证:$S_{△ABC}=S_{△ADE}$.
思维拓展:
(3)如图③,在$Rt△ABC$中,$∠C=90^{\circ },∠BAC$和$∠ABC$的平分线AD与BE相交于点F,连接DE,$S_{△ABC}=30,S_{△CDE}=4$,则$S_{△ABF}=$____.

答案：

(1) 1 ＜ AD ＜ 5 解析：如图①，延长AD至点E，使DE = AD，连接BE，
　
∵ 点D为BC的中点，
∴ BD = CD。在△BDE和△CDA中，$\begin{cases} BD = CD \\ ∠BDE = ∠CDA \\ DE = DA \end{cases}$，
　　　　　　　　　　　　　　　　　　　　
∴ △BDE ≌ △CDA(SAS)，
∴ BE = CA = 4，
∴ AB - BE ＜ AE ＜ AB + BE，
∴ 2 ＜ AE ＜ 10，
∴ 1 ＜ AD ＜ 5。
(2) 如图②，延长AF至点G，使FG = AF，连接CG，
∵ ∠BAD = ∠CAE = 90°，
∴ ∠DAE + ∠BAC = 180°，
∴ ∠DAE + ∠BAF + ∠CAF = 180°。
∵ 点F为BC的中点，
∴ BF = CF，在△ABF和△GCF中，$\begin{cases} AF = GF \\ ∠AFB = ∠GFC \\ BF = CF \end{cases}$，
　　　　　　　　　　　　　　　　　　　　
∴ △ABF ≌ △GCF(SAS)，
∴ ∠BAF = ∠CGF，AB = CG = AD，$S_{△ABF} = S_{△GCF}$。
∵ ∠DAE + ∠BAF + ∠CAF = 180°，
∴ ∠DAE + ∠CGF + ∠CAF = 180°。
∵ ∠ACG + ∠CGF + ∠CAF = 180°，
∴ ∠DAE = ∠GCA。在△ADE和△CGA中，$\begin{cases} AD = CG \\ ∠DAE = ∠GCA \\ AE = CA \end{cases}$，
∴ △ADE ≌ △CGA(SAS)，
∴ $S_{△ADE} = S_{△CGA}$。
∵ $S_{△CGA} = S_{△ACF} + S_{△GCF} = S_{△ACF} + S_{△ABF} = S_{△ABC}$，
∴ $S_{△ABC} = S_{△ADE}$。
(3) 13 解析：如图③，
∵ BE，AD分别平分∠ABC，∠BAC。
∴ ∠1 = ∠2 = $\frac{1}{2}$∠ABC，∠3 = ∠4 = $\frac{1}{2}$∠BAC。
∵ ∠ACB = 90°，
∴ ∠ABC + ∠BAC = 90°，
∴ ∠1 + ∠3 = $\frac{1}{2}$(∠ABC + ∠BAC) = 45°，
∴ ∠5 = ∠8 = ∠1 + ∠3 = 45°。在AB上截取BM = BD，AN = AE，连接FM，FN，
　　　　　　　　　　
在△AFE和△AFN中，$\begin{cases} AE = AN \\ ∠4 = ∠3 \\ AF = AF \end{cases}$，
∴ △AFE ≌ △AFN(SAS)，同理可得△BFD ≌ △BFM(SAS)，
∴ DF = FM，EF = FN，∠5 = ∠6 = ∠7 = ∠8 = 45°，$S_{△AFE} = S_{△AFN}$，$S_{△BDF} = S_{△BFM}$。过点N作NP ⊥ MF于点P，过点E作EQ ⊥ AF于点Q，则∠NPF = ∠EQF = 90°。又
∵ ∠NFP = 180° - 45° - 45° - 45° = 45°，EF = FN，
∴ △NFP ≌ △EFQ(AAS)，
∴ NP = EQ，
∴ $S_{△MFN} = \frac{1}{2} \times FM \times NP = \frac{1}{2} \times DF \times EQ = S_{△DEF}$。又
∵ $S_{△ABC} - S_{△CDE} = 30 - 4 = 26 = S_{△DFE} + S_{△BDF} + S_{△AFE} + S_{△ABF} = S_{△BFM} + S_{△MFN} + S_{△ANF} + S_{△ABF} = 2S_{△ABF}$，
∴ $S_{△ABF} = 13$。