《2025年学霸题中题八年级数学上册人教版》

1. 教材P19活动2变式 将一个六边形进行三角剖分,即用对角线将它剖分成互不重叠的4个三角形,那么各种不同的剖分方法种数是(D)
A. 6
B. 8
C. 12
D. 14

答案： D

2. 改编题 如图,$BA_{1}$和$CA_{1}$分别是$\triangle ABC$的内角平分线和外角平分线,$BA_{2}$是$∠A_{1}BD$的平分线,$CA_{2}$是$∠A_{1}CD$的平分线,$BA_{3}$是$∠A_{2}BD$的平分线,$CA_{3}$是$∠A_{2}CD$的平分线,…,若$∠A=α$,则$∠A_{999}=$____.

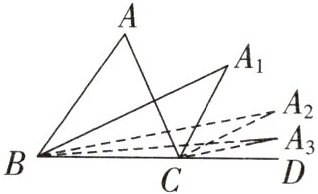
答案：
$\frac{α}{2^{999}}$ 解析:
∵ $BA_{1}$ 是 $∠ABC$ 的平分线，$CA_{1}$ 是 $∠ACD$ 的平分线，
∴ $∠A_{1}BC=\frac{1}{2}∠ABC$，$∠A_{1}CD=\frac{1}{2}∠ACD$。又
∵ $∠ACD=∠A+∠ABC$，$∠A_{1}CD=∠A_{1}BC+∠A_{1}$，
∴ $\frac{1}{2}(∠A+∠ABC)=\frac{1}{2}∠ABC+∠A_{1}$，
∴ $∠A_{1}=\frac{1}{2}∠A$。
∵ $∠A=α$，
∴ $∠A_{1}=\frac{1}{2}α$。同理可得 $∠A_{2}=\frac{1}{2}∠A_{1}=\frac{1}{4}α=\frac{α}{2^{2}}$，$∠A_{3}=\frac{1}{2}∠A_{2}=\frac{1}{8}α=\frac{α}{2^{3}}$，…，则 $∠A_{999}=\frac{α}{2^{999}}$。
归纳总结
如图，$∠ABC$，$∠ACD$ 的平分线 $BA_{1}$，$CA_{1}$ 相交于点 $A_{1}$；$∠A_{1}BC$，$∠A_{1}CD$ 的平分线 $BA_{2}$，$CA_{2}$ 相交于点 $A_{2}$，…，$∠A_{n-1}BC$，$∠A_{n-1}CD$ 的平分线 $BA_{n}$，$CA_{n}$ 相交于点 $A_{n}$ 得到 $∠A_{n}$，则 $∠A_{n}=\frac{1}{2^{n}}∠A$。

3. (2024·盐城月考)如图,对$\triangle ABC$逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点$A_{1},B_{1},C_{1}$,使得$A_{1}B=2AB,B_{1}C=2BC,C_{1}A=2CA$,顺次连接$A_{1},B_{1},C_{1}$,得到$\triangle A_{1}B_{1}C_{1}$,记其面积为$S_{1}$;第二次操作,分别延长$A_{1}B_{1},B_{1}C_{1},C_{1}A_{1}$至点$A_{2},B_{2},C_{2}$,使得$A_{2}B_{1}=2A_{1}B_{1},B_{2}C_{1}=2B_{1}C_{1},C_{2}A_{1}=2C_{1}A_{1}$,顺次连接$A_{2},B_{2},C_{2}$,得到$\triangle A_{2}B_{2}C_{2}$,记其面积为$S_{2}$;…;按此规律继续下去,可得到$\triangle A_{6}B_{6}C_{6}$,若$S_{6}=a$,则$S_{\triangle ABC}=$____.(结果用含a的代数式表示)

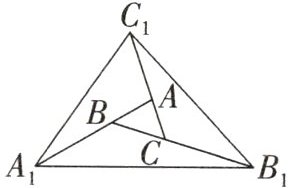
答案：
$\frac{a}{19^{6}}$ 解析:连接 $A_{1}C$，$B_{1}A$，$C_{1}B$，如图，设 $S_{△ABC}=s$，
∵ $A_{1}B=2AB$，
∴ $AA_{1}=3AB$。
∵ $△ABC$ 中 $AB$ 边上的高与 $△AA_{1}C$ 中 $A_{1}A$ 边上的高相同，
∴ $\frac {S_{△AA_{1}C}}{S_{△ABC}}=\frac {AA_{1}}{AB}=\frac {3}{1}$，
∴ $S_{△AA_{1}C}=3S_{△ABC}=3s$。
∵ $C_{1}A=2CA$，$△AA_{1}C$ 中 $AC$ 边上的高与 $△A_{1}AC_{1}$ 中 $C_{1}A$ 边上的高相同，
∴ $S_{△AA_{1}C_{1}}=2S_{△AA_{1}C}=6s$，同理可得，$S_{△A_{1}B_{1}B}=6s$，$S_{△C_{1}B_{1}C}=6s$，
∴ $S_{△A_{1}B_{1}C_{1}}=S_{△AA_{1}C_{1}}+S_{△A_{1}B_{1}B}+S_{△C_{1}B_{1}C}+S_{△ABC}=6s×3+s=19s$。同理得 $S_{△A_{2}B_{2}C_{2}}=6×19s×3+19s=19s×19=19^{2}s$，$S_{△A_{3}B_{3}C_{3}}=19^{2}s×19=19^{3}s$，$S_{△A_{4}B_{4}C_{4}}=19^{3}s×19=19^{4}s$，$S_{△A_{5}B_{5}C_{5}}=19^{4}s×19=19^{5}s$，$S_{△A_{6}B_{6}C_{6}}=19^{5}s×19=19^{6}s$。
∵ $S_{6}=a$，
∴ $19^{6}s=a$，解得 $s=\frac{a}{19^{6}}$，即 $S_{△ABC}=\frac{a}{19^{6}}$。

4. (2025·郑州期末)在学习数学知识的过程中,我们经历过很多次“归纳”的过程,即从几种特殊情形出发,进而找到一般规律的过程.数学活动课上,同学们利用“归纳”策略探究“十二边形内有30个点(任意三点不共线),将这30个点与十二边形的顶点相连可以把十二边形分割成多少个三角形(互相不重叠)”的问题.小明认为可以先从最简单的三角形进行研究,先研究三角形内有1个点、2个点、3个点……的情形(如下图):

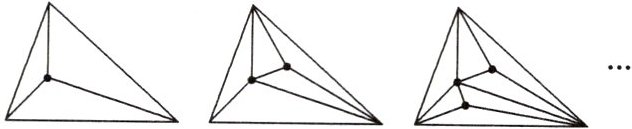
填写数据:
|三角形内点的个数|1|2|3|4|5|…|
|----|----|----|----|----|----|----|
|分割成的三角形的个数|3|5|7|a|11|…|
再分别研究四边形、五边形、六边形……内有1个点、2个点、3个点……的情形.根据小明的研究思路,解答下列问题:
(1)表中$a=$____.
(2)发现规律,当三角形内点的个数增加1,分割成三角形的个数就会增加____:当三角形内有n个点时,分割成____个三角形.
(3)当三角形内有30个点时,分割成多少个三角形?原三角形被若干个点分割成三角形的个数可能是2024吗?为什么?
(4)直接写出当四边形内有30个点时,分割成多少个三角形?当十二边形内有30个点时,分割成多少个三角形?

答案：

(1) 9 解析:依题意，根据表格数据得 $3+2×(1-1)=3$，$3+2×(2-1)=5$，$3+2×(3-1)=7$，$3+2×(5-1)=11$，
∴ $a=3+2×(4-1)=9$。
(2) 2 $(2n+1)$ 解析:发现规律，当三角形内点的个数增加 1，分割成三角形的个数就会增加 2，与
(1)同理得当三角形内有 $n$ 个点时，分割成 $3+2(n-1)=(2n+1)$ 个三角形。
(3)
∵ 由
(2)得当三角形内有 $n$ 个点时，分割成 $(2n+1)$ 个三角形，把 $n=30$ 代入 $2n+1$，得 $2×30+1=61$，
∴ 当三角形内有 30 个点时，分割成 61 个三角形。原三角形被若干个点分割成三角形的个数不可能是 2024。理由如下:
∵ $2n+1=2024$，解得 $n=\frac{2023}{2}$，不是正整数，
∴ 原三角形被若干个点分割成三角形的个数不可能是 2024。
(4) 当四边形内有 30 个点时，分割成 62 个三角形；当十二边形内有 30 个点时，分割成 70 个三角形。 解析:如图，四边形 $ABCD$ 内部有若干个点，用这些点以及四边形 $ABCD$ 的顶点 $A$，$B$，$C$，$D$ 把原四边形分割成一些三角形(互相不重叠):
　　 　
则把 $n=30$ 代入 $2n+2$，得 $2n+2=2×30+2=62$，即当四边形内有 30 个点时，分割成 62 个三角形；观察题干的表格数据，用三角形以及四边形来研究，可得出当点数相同，$r$ 边形分割成的三角形的个数是三角形分割成的三角形的个数 $+(r-3)$，即 $61+(12-3)=70$，
∴ 当十二边形内有 30 个点时，分割成 70 个三角形。