《2025年学霸题中题八年级数学上册人教版》

12.已知长方形的长为$a$,宽为$b$,周长为16,长与宽的平方和为34.
(1)求此长方形的面积;
(2)求$a b ^ { 3 } + 2 a ^ { 2 } b ^ { 2 } + a ^ { 3 } b$的值.

答案：
(1) $\because a + b = 16 \div 2 = 8$, $\therefore a^2 + 2ab + b^2 = 64$. $\because a^2 + b^2 = 34$, $\therefore ab = 15$, 即长方形的面积为 15.
(2) $ab^3 + 2a^2b^2 + a^3b = ab(a^2 + 2ab + b^2) = ab(a + b)^2 = 15 \times 8^2 = 960$.

13.新趋势 数学文化阅读与证明:请阅读以下材料,并完成相应的任务.
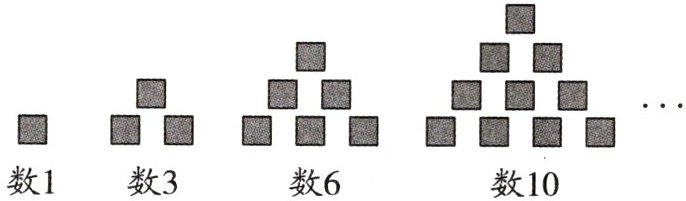
传说古希腊毕达哥拉斯(约公元前580年~约前500(490)年)学派的数学家经常在沙滩上研究数学问题.他们在沙滩上画点或用小石子来表示数,比如,他们研究过1,3,6,10,…,由于这些数可以用图中所示的三角形点阵表示,他们就将其称为三角形数,第$n$个三角形数可以用$\frac { n ( n + 1 ) } { 2 } ( n \geq 1 )$表示.
任务:请根据以上材料,证明以下结论:
(1)任意一个三角形数乘8再加1是一个整数的平方;
(2)连续两个三角形数的和是一个整数的平方.

答案：
(1) 由题意知, 第 $n$ 个三角形数为 $\frac{n(n + 1)}{2}$, $\therefore \frac{n(n + 1)}{2} \times 8 + 1 = 4n^2 + 4n + 1 = (2n + 1)^2$, $\therefore$ 任意一个三角形数乘 8 再加 1 是一个整数的平方.
(2) $\because$ 第 $n$ 个三角形数为 $\frac{n(n + 1)}{2}$, 第 $(n + 1)$ 个三角形数为 $\frac{(n + 1)(n + 2)}{2}$, $\therefore \frac{n(n + 1)}{2} + \frac{(n + 1)(n + 2)}{2} = \frac{1}{2}(n^2 + n + n^2 + 3n + 2) = n^2 + 2n + 1 = (n + 1)^2$, $\therefore$ 连续两个三角形数的和是一个整数的平方.

14.已知$x - y = a$,$z - y = 10$,则$x ^ { 2 } + y ^ { 2 } + z ^ { 2 } - x y - y z - z x$的最小值为____75.

答案： 75 解析: $\because x - y = a$, $z - y = 10$, $\therefore x - z = a - 10$, 原式 $= \frac{1}{2}(2x^2 + 2y^2 + 2z^2 - 2xy - 2yz - 2zx) = \frac{1}{2}[(x - y)^2 + (z - y)^2 + (x - z)^2] = \frac{1}{2}[a^2 + 100 + (a - 10)^2] = \frac{1}{2}(2a^2 - 20a + 200) = a^2 - 10a + 100 = (a - 5)^2 + 75$, $\therefore$ 当 $a = 5$ 时, 原式的最小值为 75.

15.改编题我们可以采用下面的方法分解因式:$a ^ { 2 } + 6 a + 8 = a ^ { 2 } + 6 a + 9 - 1 = ( a + 3 ) ^ { 2 } - 1 = ( a + 2 ) ( a + 4 )$.像这样,先添一适当项,使之出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”.
利用“配方法”进行因式分解:
(1)$x ^ { 2 } - 6 x - 27$;$x^2 - 6x - 27 = x^2 - 6x + 9 - 36 = (x - 3)^2 - 6^2 = (x - 3 + 6)(x - 3 - 6) = (x + 3)(x - 9)$
(2)$a ^ { 2 } + 3 a - 28$;$a^2 + 3a - 28 = a^2 + 3a + (\frac{3}{2})^2 - (\frac{3}{2})^2 - 28 = (a + \frac{3}{2})^2 - \frac{121}{4} = (a + \frac{3}{2} - \frac{11}{2})(a + \frac{3}{2} + \frac{11}{2}) = (a - 4)(a + 7)$
(3)$x ^ { 2 } - ( 2 n + 1 ) x + n ^ { 2 } + n$;$x^2 - (2n + 1)x + n^2 + n = x^2 - (2n + 1)x + (n + \frac{1}{2})^2 - (n + \frac{1}{2})^2 + n^2 + n = (x - n - \frac{1}{2})^2 - (\frac{1}{2})^2 = (x - n - \frac{1}{2} - \frac{1}{2})(x - n - \frac{1}{2} + \frac{1}{2}) = (x - n - 1)(x - n)$
(4)$a ^ { 4 } + a ^ { 2 } b ^ { 2 } + b ^ { 4 }$.$a^4 + a^2b^2 + b^4 = a^4 + a^2b^2 + b^4 + a^2b^2 - a^2b^2 = (a^2 + b^2)^2 - a^2b^2 = (a^2 + b^2 + ab)(a^2 + b^2 - ab)$

答案：
(1) $x^2 - 6x - 27 = x^2 - 6x + 9 - 36 = (x - 3)^2 - 6^2 = (x - 3 + 6)(x - 3 - 6) = (x + 3)(x - 9)$.
(2) $a^2 + 3a - 28 = a^2 + 3a + (\frac{3}{2})^2 - (\frac{3}{2})^2 - 28 = (a + \frac{3}{2})^2 - \frac{121}{4} = (a + \frac{3}{2} - \frac{11}{2})(a + \frac{3}{2} + \frac{11}{2}) = (a - 4)(a + 7)$.
(3) $x^2 - (2n + 1)x + n^2 + n = x^2 - (2n + 1)x + (n + \frac{1}{2})^2 - (n + \frac{1}{2})^2 + n^2 + n = (x - n - \frac{1}{2})^2 - (\frac{1}{2})^2 = (x - n - \frac{1}{2} - \frac{1}{2})(x - n - \frac{1}{2} + \frac{1}{2}) = (x - n - 1)(x - n)$.
(4) $a^4 + a^2b^2 + b^4 = a^4 + a^2b^2 + b^4 + a^2b^2 - a^2b^2 = (a^2 + b^2)^2 - a^2b^2 = (a^2 + b^2 + ab)(a^2 + b^2 - ab)$.