《2025年高考帮数学》

训练2 《九章算术》中有一种几何体叫做刍甍(méng)(底面为矩形的屋脊状楔体)，如图是一个刍甍，四边形EFBA为等腰梯形，EF//AB，FB = FC = √3，AB = 2EF = 2BC = 4，则此刍甍的表面积为_______.
　　　　　　　　　　　

答案：
8 + 8$\sqrt{2}$ 如图所示,过点F作FG⊥AB于G,FH⊥BC于H.因为FB = FC = $\sqrt{3}$,BC = 2,所以H为BC的中点,易得FH = $\sqrt{2}$,所以$S_{\triangle FBC}$ = $S_{\triangle EAD}$ = $\sqrt{2}$.因为四边形EFBA为等腰梯形,且AB = 2EF = 4,所以易得FG = $\sqrt{2}$,所以$S_{梯形EFBA}$ = $S_{梯形EFCD}$ = $\frac{1}{2}$×(2 + 4)×$\sqrt{2}$ = 3$\sqrt{2}$,所以此刍甍的表面积S = 2×4 + 2×$\sqrt{2}$ + 2×3$\sqrt{2}$ = 8 + 8$\sqrt{2}$.

例5 (1)[2023全国卷乙]已知圆锥PO的底面半径为√3，O为底面圆心，PA，PB为圆锥的母线，∠AOB = 2π/3，若△PAB的面积等于9√3/4，则该圆锥的体积为 (　　　)
A. π
B. √6π
C. 3π
D. 3√6π

答案：
(1)B 在△AOB中,AO = BO = $\sqrt{3}$,∠AOB = $\frac{2\pi}{3}$,由余弦定理得AB = $\sqrt{3 + 3 - 2\times\sqrt{3}\times\sqrt{3}\times(-\frac{1}{2})}$ = 3,设等腰三角形PAB底边AB上的高为h,则$S_{\triangle PAB}$ = $\frac{1}{2}$×3h = $\frac{9\sqrt{3}}{4}$,解得h = $\frac{3\sqrt{3}}{2}$,由勾股定理得母线PA = $\sqrt{(\frac{3}{2})^{2}+(\frac{3\sqrt{3}}{2})^{2}}$ = 3,则该圆锥的高PO = $\sqrt{PA^{2}-OA^{2}}$ = $\sqrt{6}$,所以该圆锥的体积为$\frac{1}{3}$×3π×$\sqrt{6}$ = $\sqrt{6}$π,故选B.

(2)[2023天津高考]在三棱锥P - ABC中，线段PC上的点M满足PM = 1/3PC，线段PB上的点N满足PN = 2/3PB，则三棱锥P - AMN和三棱锥P - ABC的体积之比为 (　　　)
A. 1/9
B. 2/9
C. 1/3
D. 4/9

答案：

(2)B 如图,因为PM = $\frac{1}{3}$PC,PN = $\frac{2}{3}$PB,所以$\frac{S_{\triangle PMN}}{S_{\triangle PBC}}$ = $\frac{\frac{1}{2}PM\cdot PN\cdot\sin\angle BPC}{\frac{1}{2}PC\cdot PB\cdot\sin\angle BPC}$ = $\frac{PM\cdot PN}{PC\cdot PB}$ = $\frac{1}{3}$×$\frac{2}{3}$ = $\frac{2}{9}$,所以$\frac{V_{三棱锥P - AMN}}{V_{三棱锥P - ABC}}$ = $\frac{V_{三棱锥A - PMN}}{V_{三棱锥P - PBC}}$ = $\frac{\frac{1}{3}S_{\triangle PMN}\cdot d}{\frac{1}{3}S_{\triangle PBC}\cdot d}$ = $\frac{S_{\triangle PMN}}{S_{\triangle PBC}}$ = $\frac{2}{9}$(其中d为点A到平面PBC的距离,因为平面PMN和平面PBC重合,所以点A到平面PMN的距离也是d).故选B.

训练3 (1)十字歇山顶是中国古代建筑屋顶的经典样式之一，图1中的故宫角楼的顶部即为十字歇山顶. 其上部可视为由两个相同的直三棱柱交叠而成的几何体(图2). 这两个直三棱柱有一个公共侧面ABCD. 在底面BCE中，若BE = CE = 3，∠BEC = 120°，则该几何体的体积为 (　　　)
　
　　　　　　　
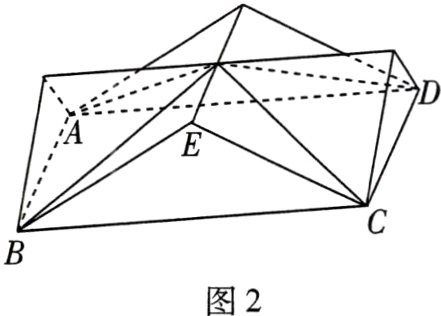
A. 27/2
B. 27√3/2
C. 27
D. 27√3
(2)[2023新高考卷I]在正四棱台ABCD - A₁B₁C₁D₁中，AB = 2，A₁B₁ = 1，AA₁ = √2，则该棱台的体积为_______.

答案：

(1)C 如图所示,该几何体可视为由直三棱柱BCE - ADF与两个三棱锥G - MAB,G - NCD拼接而成.记直三棱柱BCE - ADF的高为h,底面BCE的面积为S,所求几何体的体积为V,则S = $\frac{1}{2}$BE×CE×sin 120° = $\frac{1}{2}$×3×3×$\frac{\sqrt{3}}{2}$ = $\frac{9\sqrt{3}}{4}$,h = CD = BC = 3$\sqrt{3}$.所以V = $V_{三棱柱BCE - ADF}$ + $V_{三棱锥G - MAB}$ + $V_{三棱锥G - NCD}$ = Sh + $\frac{1}{3}$S×$\frac{1}{2}$h + $\frac{1}{3}$S×$\frac{1}{2}$h = $\frac{4}{3}$Sh = 27.故选C.
@@
(2)$\frac{7\sqrt{6}}{6}$ 如图所示,设点O₁,O分别为正四棱台ABCD - A₁B₁C₁D₁上、下底面的中心,连接B₁D₁,BD,则点O₁,O分别为B₁D₁,BD的中点,连接O₁O,则O₁O即正四棱台ABCD - A₁B₁C₁D₁的高,过点B₁作B₁E⊥BD,垂足为E,则B₁E = O₁O.因为AB = 2,A₁B₁ = 1,所以OB = $\sqrt{2}$,O₁B₁ = $\frac{\sqrt{2}}{2}$,所以BE = OB - OE = OB - O₁B₁ = $\frac{\sqrt{2}}{2}$,又AA₁ = $\sqrt{2}$,所以BB₁ = $\sqrt{2}$,B₁E = $\sqrt{BB_{1}^{2}-BE^{2}}$ = $\sqrt{2-\frac{1}{2}}$ = $\frac{\sqrt{6}}{2}$,所以O₁O = $\frac{\sqrt{6}}{2}$,所以$V_{正四棱台ABCD - A_{1}B_{1}C_{1}D_{1}}$ = $\frac{1}{3}$×(2² + 1² + $\sqrt{2^{2}\times1^{2}}$)×$\frac{\sqrt{6}}{2}$ = $\frac{7\sqrt{6}}{6}$.

例6 [2022全国卷乙]已知球O的半径为1，四棱锥的顶点为O，底面的四个顶点均在球O的球面上，则当该四棱锥的体积最大时，其高为 (　　　)
A. 1/3
B. 1/2
C. √3/3
D. √2/2

答案： C 该四棱锥的体积最大即该四棱锥底面所在圆面和顶点O组成的圆锥体积最大.设圆锥的高为h(0 ＜ h ＜ 1),底面半径为r,则圆锥的体积V = $\frac{1}{3}$πr²h = $\frac{1}{3}$π(1 - h²)h,则V' = $\frac{1}{3}$π(1 - 3h²),令V' = 0,得h = $\frac{\sqrt{3}}{3}$,所以V = $\frac{1}{3}$π(1 - h²)h在(0,$\frac{\sqrt{3}}{3}$)上单调递增,在($\frac{\sqrt{3}}{3}$,1)上单调递减,所以当h = $\frac{\sqrt{3}}{3}$时,四棱锥的体积最大,故选C.

训练4 [2023湖北省宜昌市三校联考]已知正方体ABCD - A₁B₁C₁D₁的棱长为√3，点E为棱D₁C₁上一动点，点F为BB₁上一动点，且满足EF = 2，则三棱锥B₁ - EFC₁的体积的最大值为_______.

答案：
$\frac{\sqrt{3}}{12}$ 如图,不妨设C₁E = m(0 ＜ m ≤ $\sqrt{3}$),B₁F = n(0 ＜ n ≤ $\sqrt{3}$),则EF = $\sqrt{C_{1}E^{2}+B_{1}C^{2}+B_{1}F^{2}}$ = $\sqrt{m^{2}+(\sqrt{3})^{2}+n^{2}}$ = 2,所以m² + n² = 1.于是$V_{三棱锥B_{1}-EFC_{1}}$ = $V_{三棱锥F - B_{1}EC_{1}}$ = $\frac{1}{3}$$S_{\triangle B_{1}EC_{1}}$×B₁F = $\frac{1}{3}$×$\frac{1}{2}$×m×$\sqrt{3}$×n = $\frac{\sqrt{3}}{6}$mn ≤ $\frac{\sqrt{3}}{6}$×$\frac{m^{2}+n^{2}}{2}$ = $\frac{\sqrt{3}}{12}$,当且仅当m = n = $\frac{\sqrt{2}}{2}$时等号成立.故三棱锥B₁ - EFC₁的体积的最大值为$\frac{\sqrt{3}}{12}$.