2025年高考帮数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高考帮数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
训练3 [2022新高考卷Ⅰ]记 为数列{
为数列{ }的前n项和,已知
}的前n项和,已知 = 1,
= 1, 是公差为
是公差为 的等差数列。
的等差数列。
(1)求{ }的通项公式。
}的通项公式。
(2)证明: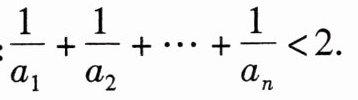
 为数列{
为数列{ }的前n项和,已知
}的前n项和,已知 = 1,
= 1, 是公差为
是公差为 的等差数列。
的等差数列。(1)求{
 }的通项公式。
}的通项公式。(2)证明:
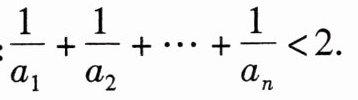
答案:
训练3
(1)因为$a_{1}=1$,所以$\frac{S_{1}}{a_{1}}=1$,又$\{\frac{S_{n}}{a_{n}}\}$是公差为$\frac{1}{3}$的等差数列,所以$\frac{S_{n}}{a_{n}}=1+(n - 1)\times\frac{1}{3}=\frac{n + 2}{3}$。所以$S_{n}=\frac{n + 2}{3}a_{n}$。因为当$n\geqslant2$时,$a_{n}=S_{n}-S_{n - 1}=\frac{n + 2}{3}a_{n}-\frac{n + 1}{3}a_{n - 1}$,所以$\frac{n + 1}{3}a_{n - 1}=\frac{n - 1}{3}a_{n}(n\geqslant2)$,所以$\frac{a_{n}}{a_{n - 1}}=\frac{n + 1}{n - 1}(n\geqslant2)$,所以$\frac{a_{2}}{a_{1}}\times\frac{a_{3}}{a_{2}}\times\cdots\times\frac{a_{n - 1}}{a_{n - 2}}\times\frac{a_{n}}{a_{n - 1}}=\frac{3}{1}\times\frac{4}{2}\times\cdots\times\frac{n}{n - 2}\times\frac{n + 1}{n - 1}=\frac{n(n + 1)}{2}(n\geqslant2)$,所以$a_{n}=\frac{n(n + 1)}{2}(n\geqslant2)$,又$a_{1}=1$也满足上式,所以$a_{n}=\frac{n(n + 1)}{2}(n\in\mathbf{N}^{*})$。
(2)因为$a_{n}=\frac{n(n + 1)}{2}$,所以$\frac{1}{a_{n}}=\frac{2}{n(n + 1)}=2(\frac{1}{n}-\frac{1}{n + 1})$,所以$\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}=2[(1 - \frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+\cdots+(\frac{1}{n}-\frac{1}{n + 1})]=2(1 - \frac{1}{n + 1})<2$。
(1)因为$a_{1}=1$,所以$\frac{S_{1}}{a_{1}}=1$,又$\{\frac{S_{n}}{a_{n}}\}$是公差为$\frac{1}{3}$的等差数列,所以$\frac{S_{n}}{a_{n}}=1+(n - 1)\times\frac{1}{3}=\frac{n + 2}{3}$。所以$S_{n}=\frac{n + 2}{3}a_{n}$。因为当$n\geqslant2$时,$a_{n}=S_{n}-S_{n - 1}=\frac{n + 2}{3}a_{n}-\frac{n + 1}{3}a_{n - 1}$,所以$\frac{n + 1}{3}a_{n - 1}=\frac{n - 1}{3}a_{n}(n\geqslant2)$,所以$\frac{a_{n}}{a_{n - 1}}=\frac{n + 1}{n - 1}(n\geqslant2)$,所以$\frac{a_{2}}{a_{1}}\times\frac{a_{3}}{a_{2}}\times\cdots\times\frac{a_{n - 1}}{a_{n - 2}}\times\frac{a_{n}}{a_{n - 1}}=\frac{3}{1}\times\frac{4}{2}\times\cdots\times\frac{n}{n - 2}\times\frac{n + 1}{n - 1}=\frac{n(n + 1)}{2}(n\geqslant2)$,所以$a_{n}=\frac{n(n + 1)}{2}(n\geqslant2)$,又$a_{1}=1$也满足上式,所以$a_{n}=\frac{n(n + 1)}{2}(n\in\mathbf{N}^{*})$。
(2)因为$a_{n}=\frac{n(n + 1)}{2}$,所以$\frac{1}{a_{n}}=\frac{2}{n(n + 1)}=2(\frac{1}{n}-\frac{1}{n + 1})$,所以$\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}=2[(1 - \frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+\cdots+(\frac{1}{n}-\frac{1}{n + 1})]=2(1 - \frac{1}{n + 1})<2$。
例4 已知函数f(x) = x + sin πx - 3,则f( 1 / 2025 ) + f( 2 / 2025 ) + f( 3 / 2025 ) + ⋯ + f( 4048 / 2025 ) + f( 4049 / 2025 ) = ________。
答案:
- 8098 令$y = f(\frac{1}{2025})+f(\frac{2}{2025})+\cdots + f(\frac{4048}{2025})+f(\frac{4049}{2025})$ ①,$y = f(\frac{4049}{2025})+f(\frac{4048}{2025})+\cdots + f(\frac{2}{2025})+f(\frac{1}{2025})$ ②,①+②,得$2y=[f(\frac{1}{2025})+f(\frac{4049}{2025})]+[f(\frac{2}{2025})+f(\frac{4048}{2025})]+\cdots+[f(\frac{4048}{2025})+f(\frac{2}{2025})]+[f(\frac{4049}{2025})+f(\frac{1}{2025})]$。因为$f(x)+f(2 - x)=x+\sin\pi x - 3+(2 - x)+\sin[\pi(2 - x)]-3=-4$,所以$2y=-4\times4049$,故$y=-8098$。
训练4 已知数列{ }的通项
}的通项 = (2n - 100) / (2n - 101),则a₁ + a₂ + ⋯ + a₁₀₀ = ( )
= (2n - 100) / (2n - 101),则a₁ + a₂ + ⋯ + a₁₀₀ = ( )
A.98
B.99
C.100
D.101
 }的通项
}的通项 = (2n - 100) / (2n - 101),则a₁ + a₂ + ⋯ + a₁₀₀ = ( )
= (2n - 100) / (2n - 101),则a₁ + a₂ + ⋯ + a₁₀₀ = ( )A.98
B.99
C.100
D.101
答案:
C 因为$a_{n}=\frac{2n - 100}{2n - 101}$,所以$a_{n}+a_{101 - n}=\frac{2n - 100}{2n - 101}+\frac{2(101 - n)-100}{2(101 - n)-101}=\frac{2n - 100}{2n - 101}+\frac{102 - 2n}{101 - 2n}=\frac{4n - 202}{2n - 101}=2$,所以$a_{1}+a_{100}=a_{2}+a_{99}=\cdots=a_{100}+a_{1}=2$,所以$a_{1}+a_{2}+\cdots + a_{100}=50\times2=100$。
例1 [全国卷II]已知数列$\{ a_{n}\}$和$\{ b_{n}\}$满足$a_{1}=1,b_{1}=0,4a_{n + 1}=3a_{n}-b_{n}+4,4b_{n + 1}=3b_{n}-a_{n}-4$.
(1)证明:$\{ a_{n}+b_{n}\}$是等比数列,$\{ a_{n}-b_{n}\}$是等差数列.
(2)求$\{ a_{n}\}$和$\{ b_{n}\}$的通项公式.
(1)证明:$\{ a_{n}+b_{n}\}$是等比数列,$\{ a_{n}-b_{n}\}$是等差数列.
(2)求$\{ a_{n}\}$和$\{ b_{n}\}$的通项公式.
答案:
(1)由题设得4(a_{n + 1}+b_{n + 1}) = 2(a_{n}+b_{n}),即a_{n + 1}+b_{n + 1}=\frac{1}{2}(a_{n}+b_{n})。因为a_{1}+b_{1}=1,所以{a_{n}+b_{n}}是首项为1,公比为\frac{1}{2}的等比数列。
由题设得4(a_{n + 1}-b_{n + 1}) = 4(a_{n}-b_{n}) + 8,即a_{n + 1}-b_{n + 1}=a_{n}-b_{n}+2。因为a_{1}-b_{1}=1,所以{a_{n}-b_{n}}是首项为1,公差为2的等差数列。
(2)由
(1)知,a_{n}+b_{n}=\frac{1}{2^{n - 1}},a_{n}-b_{n}=2n - 1,
所以a_{n}=\frac{1}{2}[(a_{n}+b_{n})+(a_{n}-b_{n})]=\frac{1}{2^{n}}+n-\frac{1}{2},
b_{n}=\frac{1}{2}[(a_{n}+b_{n})-(a_{n}-b_{n})]=\frac{1}{2^{n}}-n+\frac{1}{2}。
(1)由题设得4(a_{n + 1}+b_{n + 1}) = 2(a_{n}+b_{n}),即a_{n + 1}+b_{n + 1}=\frac{1}{2}(a_{n}+b_{n})。因为a_{1}+b_{1}=1,所以{a_{n}+b_{n}}是首项为1,公比为\frac{1}{2}的等比数列。
由题设得4(a_{n + 1}-b_{n + 1}) = 4(a_{n}-b_{n}) + 8,即a_{n + 1}-b_{n + 1}=a_{n}-b_{n}+2。因为a_{1}-b_{1}=1,所以{a_{n}-b_{n}}是首项为1,公差为2的等差数列。
(2)由
(1)知,a_{n}+b_{n}=\frac{1}{2^{n - 1}},a_{n}-b_{n}=2n - 1,
所以a_{n}=\frac{1}{2}[(a_{n}+b_{n})+(a_{n}-b_{n})]=\frac{1}{2^{n}}+n-\frac{1}{2},
b_{n}=\frac{1}{2}[(a_{n}+b_{n})-(a_{n}-b_{n})]=\frac{1}{2^{n}}-n+\frac{1}{2}。
查看更多完整答案,请扫码查看


