2026年天利38套中考试题分类九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年天利38套中考试题分类九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
4. (2025·浙江)【问题背景】
如图所示,某兴趣小组需要在正方形纸板$ABCD$上剪下机翼状纸板(阴影部分),点$E$在对角线$BD$上.
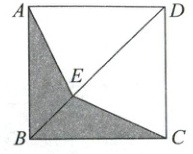
【数学理解】
(1)该机翼状纸板是由两个全等三角形组成,请写出$\triangle ABE\cong\triangle CBE$的证明过程.
(2)若裁剪过程中满足$DE=DA$,求“机翼角”$\angle BAE$的度数.
如图所示,某兴趣小组需要在正方形纸板$ABCD$上剪下机翼状纸板(阴影部分),点$E$在对角线$BD$上.

【数学理解】
(1)该机翼状纸板是由两个全等三角形组成,请写出$\triangle ABE\cong\triangle CBE$的证明过程.
(2)若裁剪过程中满足$DE=DA$,求“机翼角”$\angle BAE$的度数.
答案:
4.正方形的性质+全等三角形的判定
解:
(1)证明:如图,在正方形ABCD中,BA = BC,∠ABD = ∠CBD = 45°,
在△ABE和△CBE中,因为$\begin{cases} BA = BC, \\ \angle ABE = \angle CBE, \\ BE = BE, \end{cases}$
所以△ABE≌△CBE(SAS)。
(2)在正方形ABCD中,∠BAD = 90°,∠ADB = 45°。
因为DE = DA,
所以∠DAE = ∠DEA = 67.5°。
所以∠BAE = 90° - 67.5° = 22.5°。

4.正方形的性质+全等三角形的判定
解:
(1)证明:如图,在正方形ABCD中,BA = BC,∠ABD = ∠CBD = 45°,
在△ABE和△CBE中,因为$\begin{cases} BA = BC, \\ \angle ABE = \angle CBE, \\ BE = BE, \end{cases}$
所以△ABE≌△CBE(SAS)。
(2)在正方形ABCD中,∠BAD = 90°,∠ADB = 45°。
因为DE = DA,
所以∠DAE = ∠DEA = 67.5°。
所以∠BAE = 90° - 67.5° = 22.5°。

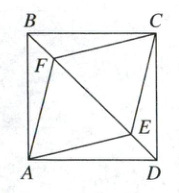
5. (2025·四川广安)如图,$E$,$F$是正方形$ABCD$的对角线$BD$上的两点,$BD=10$,$DE=BF$,连接$AE$,$AF$,$CE$,$CF$.
(1)求证:$\triangle ADE\cong\triangle CBF$.
(2)若四边形$AECF$的周长为$4\sqrt{34}$,求$EF$的长.
(1)求证:$\triangle ADE\cong\triangle CBF$.
(2)若四边形$AECF$的周长为$4\sqrt{34}$,求$EF$的长.

答案:
5.正方形的性质+全等三角形的判定与性质+勾股定理
解:
(1)证明:
∵四边形ABCD为正方形,
∴AD = BC,∠ADE = ∠CBF = 45°。
在△ADE和△CBF中,$\begin{cases} AD = BC, \\ \angle ADE = \angle CBF, \\ DE = BF, \end{cases}$
∴△ADE≌△CBF(SAS)。
(2)如图,连接AC交BD于点O(巧作辅助线:构造直角三角形),
∵四边形ABCD为正方形,BD = 10,
∴BD垂直平分AC,OA = OC = OB = $\frac{1}{2}$BD = 5。
∴AF = CF,AE = CE。
由
(1)知△ADE≌△CBF,
∴AE = CF。
∴AF = CF = AE = CE。
∵四边形AECF的周长为4$\sqrt{34}$,
∴AF = $\frac{1}{4}$×4$\sqrt{34}$ = $\sqrt{34}$。
在Rt△AOF中,OF = $\sqrt{AF^{2}-OA^{2}}$ = 3,
∴BF = DE = OB - OF = 5 - 3 = 2。
∴EF = BD - BF - DE = 6。
答:EF的长为6。

5.正方形的性质+全等三角形的判定与性质+勾股定理
解:
(1)证明:
∵四边形ABCD为正方形,
∴AD = BC,∠ADE = ∠CBF = 45°。
在△ADE和△CBF中,$\begin{cases} AD = BC, \\ \angle ADE = \angle CBF, \\ DE = BF, \end{cases}$
∴△ADE≌△CBF(SAS)。
(2)如图,连接AC交BD于点O(巧作辅助线:构造直角三角形),
∵四边形ABCD为正方形,BD = 10,
∴BD垂直平分AC,OA = OC = OB = $\frac{1}{2}$BD = 5。
∴AF = CF,AE = CE。
由
(1)知△ADE≌△CBF,
∴AE = CF。
∴AF = CF = AE = CE。
∵四边形AECF的周长为4$\sqrt{34}$,
∴AF = $\frac{1}{4}$×4$\sqrt{34}$ = $\sqrt{34}$。
在Rt△AOF中,OF = $\sqrt{AF^{2}-OA^{2}}$ = 3,
∴BF = DE = OB - OF = 5 - 3 = 2。
∴EF = BD - BF - DE = 6。
答:EF的长为6。

查看更多完整答案,请扫码查看


