2025年实验班中考数学压轴题
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班中考数学压轴题 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
1. (淮安淮安区模拟)如图,点$A(a,b)$是抛物线$y=\dfrac{1}{2}x^{2}$上位于第二象限的一动点,$OB\perp OA$交抛物线于点$B(c,d)$.当点$A$在抛物线上运动的过程中,以下结论:
①$ac$为定值;
②$ac=-bd$;
③直线$AB$必过定点$(0,1)$.
其中正确的结论有(

A.$3$个
B.$2$个
C.$1$个
D.$0$个
①$ac$为定值;
②$ac=-bd$;
③直线$AB$必过定点$(0,1)$.
其中正确的结论有(
B
).
A.$3$个
B.$2$个
C.$1$个
D.$0$个
答案:
1.B[解析]如图,过点$A$,$B$分别作$AC⊥x$轴于点$C$,$BD⊥x$轴于点$D$,
(作垂直,构造相似三角形)

则$AC = b$,$OC = - a$,$OD = c$,$BD = d$。$∵OA⊥OB$,
$∴∠AOC + ∠BOD = 90°$。$∵∠AOC + ∠OAC = 90°$,
$∴∠BOD = ∠OAC$。$∵∠ACO = ∠ODB = 90°$,$∴△OAC∽△BOD$,$∴\frac{AC}{OD}=\frac{OC}{BD}$,即$\frac{b}{c}=\frac{-a}{d}$,$∴ac = - bd$,故②正确;$∵ac = - bd$,$b = \frac{1}{2}a²$,$d = \frac{1}{2}c²$,$∴ac = -\frac{1}{4}a²c²$,$∴ac(\frac{1}{4}ac + 1)=0$,$a≠0$且$c≠0$,$∴ac = - 4$,故①正确;$∵b = \frac{1}{2}a²$,$d = \frac{1}{2}c²$,$∴A(a,\frac{1}{2}a²)$,$B(c,\frac{1}{2}c²)$,设直线$AB$的解析式为$y = mx + n$,代入$A$,$B$的坐标,得$\begin{cases}\frac{1}{2}a²=am + n\frac{1}{2}c²=cm + n\end{cases}$,解得$\begin{cases}m=\frac{1}{2}(a + c)\\n = -\frac{ac}{2}=2\end{cases}$,$∴$直线$AB$为$y=\frac{1}{2}(a + c)x + 2$,$∴$直线$AB$必过定点$(0,2)$,故③错误。故选B。
1.B[解析]如图,过点$A$,$B$分别作$AC⊥x$轴于点$C$,$BD⊥x$轴于点$D$,
(作垂直,构造相似三角形)

则$AC = b$,$OC = - a$,$OD = c$,$BD = d$。$∵OA⊥OB$,
$∴∠AOC + ∠BOD = 90°$。$∵∠AOC + ∠OAC = 90°$,
$∴∠BOD = ∠OAC$。$∵∠ACO = ∠ODB = 90°$,$∴△OAC∽△BOD$,$∴\frac{AC}{OD}=\frac{OC}{BD}$,即$\frac{b}{c}=\frac{-a}{d}$,$∴ac = - bd$,故②正确;$∵ac = - bd$,$b = \frac{1}{2}a²$,$d = \frac{1}{2}c²$,$∴ac = -\frac{1}{4}a²c²$,$∴ac(\frac{1}{4}ac + 1)=0$,$a≠0$且$c≠0$,$∴ac = - 4$,故①正确;$∵b = \frac{1}{2}a²$,$d = \frac{1}{2}c²$,$∴A(a,\frac{1}{2}a²)$,$B(c,\frac{1}{2}c²)$,设直线$AB$的解析式为$y = mx + n$,代入$A$,$B$的坐标,得$\begin{cases}\frac{1}{2}a²=am + n\frac{1}{2}c²=cm + n\end{cases}$,解得$\begin{cases}m=\frac{1}{2}(a + c)\\n = -\frac{ac}{2}=2\end{cases}$,$∴$直线$AB$为$y=\frac{1}{2}(a + c)x + 2$,$∴$直线$AB$必过定点$(0,2)$,故③错误。故选B。
2. 实验班原创 已知二次函数$y=ax^{2}+bx+c$的图象如图所示,以下结论:①$a+b+c< 0$;②$a-b+c>1$;③$abc>0$;④$4a-2b+c< 0$;⑤$8a+c< 0$.在以上$5$个结论中,其中一定成立的是
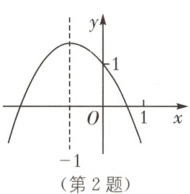
①②③⑤
.(把所有正确结论的序号都填在横线上)
答案:
2.①②③⑤[解析]由函数图象,可得各系数的关系:$a<0$,$b<0$,$c>0$,则由图象可知,①当$x = 1$时,$y = a + b + c<0$,正确;②当$x = - 1$时,$y = a - b + c>1$,正确;③$abc>0$,正确;④对称轴$x = - 1$,则$x = - 2$和$x = 0$时取值相同,则$4a - 2b + c = 1>0$,错误;⑤对称轴$x = -\frac{b}{2a}= - 1$,$b = 2a$,又$x = 2$时,$y = 4a + 2b + c<0$,代入$b = 2a$,则$8a + c<0$,正确。故所有正确结论的序号是①②③⑤。
3. (广元中考)已知抛物线$y=ax^{2}+bx+c$($a,b,c$是常数且$a\neq 0$)的自变量$x$与函数$y$的部分对应值如表:
其中$0< m< 2$.以下结论:①$abc< 0$;②若抛物线经过点$(-2,y_{1})$,$(7,y_{2})$,则$y_{2}>y_{1}$;③关于$x$的方程$\vert ax^{2}+bx+c\vert +1-s=0$有两个不相等的实数根;④$-\dfrac{16}{3}< s+n< -4$;⑤当$m=1$,$t\leqslant x\leqslant t+2$时,$y$的最小值是$1$,则$t=2$或$4$.
其中正确的结论有(

A.$1$个
B.$2$个
C.$3$个
D.$4$个
其中$0< m< 2$.以下结论:①$abc< 0$;②若抛物线经过点$(-2,y_{1})$,$(7,y_{2})$,则$y_{2}>y_{1}$;③关于$x$的方程$\vert ax^{2}+bx+c\vert +1-s=0$有两个不相等的实数根;④$-\dfrac{16}{3}< s+n< -4$;⑤当$m=1$,$t\leqslant x\leqslant t+2$时,$y$的最小值是$1$,则$t=2$或$4$.
其中正确的结论有(
C
).
A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
3.C[解析]$∵$当$x = 1$和$x = 3$时,均有$y = - 4$,
$∴$点$(1, - 4)$和点$(3, - 4)$关于对称轴对称,
(抛物线上两个不同的点,若其纵坐标相等,则它们关于抛物线的对称轴对称,反之亦成立)
$∴$抛物线的对称轴为直线$x=\frac{1 + 3}{2}=2$,
$∴$抛物线$y = ax²+bx + c(a≠0)$的对称轴为直线$x = -\frac{b}{2a}=2$,$∴b = - 4a$,
$∴$抛物线的解析式为$y = ax²-4ax + c$。
又当$x = 0$时,$y = c$,由表格可知,当$x = 0$时,$y = m$,
$∴c = m$。
$∵0<m<2$,$∴m> - 4$,$∴$抛物线的开口向上,
$∴a>0$,$c>0$,$b = - 4a<0$,$∴abc<0$,故①正确;
由①可知,抛物线$y = ax²+bx + c(a≠0)$开口向上,对称轴为直线$x = 2$。
$∵|7 - 2| = 5$,$|- 2 - 2| = 4$,$∴5>4$。
(开口向上的抛物线离对称轴越远的点对应的$y$值越大,结合抛物线对称性来理解)
$∴y₂>y₁$,故②正确;
$∵$抛物线$y = ax²+bx + c(a≠0)$开口向上,对称轴为直线$x = 2$,$∴(0,m)$与$(4,s)$关于对称轴对称,
$∴m = s$,由①可知,$m = c$,$∴m = s = c$。
$∵0<s<2$,当$s>1$时,$0<s - 1<1$,把方程$|ax²+bx + c| + 1 - s = 0$整理,得$|ax²+bx + c| = s - 1$,
$∴|ax²+bx + c| = s - 1$有$4$个根;
当$s = 1$时,方程为$|ax²+bx + c| = 0$,
$∴$方程有$2$个根;当$s<1$时,$s - 1<0$,则有$|ax²+bx + c| = s - 1<0$,
$∴$方程$|ax²+bx + c| + 1 - s = 0$无实根,故③错误;
$∵x = 2$时,$n = 4a + 2b + c$,当$x = 1$时,$a + b + c = - 4$,当$x = 3$时,$9a + 3b + c = - 4$,可得$b = - 4a$,$c = 3a - 4$,
$∴n = 4a + 2b + c = - a - 4$,$s = m = c = 3a - 4$,
$∴s + n = 2a - 8$。
$∵0<m<2$,$∴0<3a - 4<2$,解得$\frac{4}{3}<a<2$,
$∴-\frac{16}{3}<2a - 8< - 4$,故④正确;
$∵$当$m = 1$时,$m = c = s = 1$,此时抛物线过点$(0,1)$,$(4,1)$,$∴$抛物线$y = ax²+bx + 1$与$y = 1$交于点$(0,1)$,$(4,1)$。$∵t≤x≤t + 2$时,$y$的最小值为$1$,
$∴t + 2 = 0$或$t = 4$,当$t + 2 = 0$时,$t = - 2$,
$∴t = - 2$或$t = 4$,与结论$t = 2$不符合,故⑤错误。
综上所述,正确结论为①②④,共$3$个。故选C。
$∴$点$(1, - 4)$和点$(3, - 4)$关于对称轴对称,
(抛物线上两个不同的点,若其纵坐标相等,则它们关于抛物线的对称轴对称,反之亦成立)
$∴$抛物线的对称轴为直线$x=\frac{1 + 3}{2}=2$,
$∴$抛物线$y = ax²+bx + c(a≠0)$的对称轴为直线$x = -\frac{b}{2a}=2$,$∴b = - 4a$,
$∴$抛物线的解析式为$y = ax²-4ax + c$。
又当$x = 0$时,$y = c$,由表格可知,当$x = 0$时,$y = m$,
$∴c = m$。
$∵0<m<2$,$∴m> - 4$,$∴$抛物线的开口向上,
$∴a>0$,$c>0$,$b = - 4a<0$,$∴abc<0$,故①正确;
由①可知,抛物线$y = ax²+bx + c(a≠0)$开口向上,对称轴为直线$x = 2$。
$∵|7 - 2| = 5$,$|- 2 - 2| = 4$,$∴5>4$。
(开口向上的抛物线离对称轴越远的点对应的$y$值越大,结合抛物线对称性来理解)
$∴y₂>y₁$,故②正确;
$∵$抛物线$y = ax²+bx + c(a≠0)$开口向上,对称轴为直线$x = 2$,$∴(0,m)$与$(4,s)$关于对称轴对称,
$∴m = s$,由①可知,$m = c$,$∴m = s = c$。
$∵0<s<2$,当$s>1$时,$0<s - 1<1$,把方程$|ax²+bx + c| + 1 - s = 0$整理,得$|ax²+bx + c| = s - 1$,
$∴|ax²+bx + c| = s - 1$有$4$个根;
当$s = 1$时,方程为$|ax²+bx + c| = 0$,
$∴$方程有$2$个根;当$s<1$时,$s - 1<0$,则有$|ax²+bx + c| = s - 1<0$,
$∴$方程$|ax²+bx + c| + 1 - s = 0$无实根,故③错误;
$∵x = 2$时,$n = 4a + 2b + c$,当$x = 1$时,$a + b + c = - 4$,当$x = 3$时,$9a + 3b + c = - 4$,可得$b = - 4a$,$c = 3a - 4$,
$∴n = 4a + 2b + c = - a - 4$,$s = m = c = 3a - 4$,
$∴s + n = 2a - 8$。
$∵0<m<2$,$∴0<3a - 4<2$,解得$\frac{4}{3}<a<2$,
$∴-\frac{16}{3}<2a - 8< - 4$,故④正确;
$∵$当$m = 1$时,$m = c = s = 1$,此时抛物线过点$(0,1)$,$(4,1)$,$∴$抛物线$y = ax²+bx + 1$与$y = 1$交于点$(0,1)$,$(4,1)$。$∵t≤x≤t + 2$时,$y$的最小值为$1$,
$∴t + 2 = 0$或$t = 4$,当$t + 2 = 0$时,$t = - 2$,
$∴t = - 2$或$t = 4$,与结论$t = 2$不符合,故⑤错误。
综上所述,正确结论为①②④,共$3$个。故选C。
4. (绥化中考)如图,二次函数$y=ax^{2}+bx+c$与$x$轴交于点$A(3,0)$,$B(-1,0)$,与$y$轴交于点$C(0,m)$,其中$-4< m< -3$.则下列结论:
①$a-c>0$;
②方程$ax^{2}+bx+c-5=0$没有实数根;
③$-\dfrac{8}{3}< b< -2$;
④$\dfrac{a+b+c}{b-a}>0$.
其中错误的个数有(
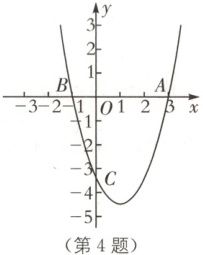
A.$1$个
B.$2$个
C.$3$个
D.$4$个
①$a-c>0$;
②方程$ax^{2}+bx+c-5=0$没有实数根;
③$-\dfrac{8}{3}< b< -2$;
④$\dfrac{a+b+c}{b-a}>0$.
其中错误的个数有(
A
).
A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
4.A[解析]二次函数$y = ax²+bx + c$与$x$轴交于点$A(3,0)$,$B(- 1,0)$,图象开口向上,
$∴$对称轴为直线$x = 1$,$a>0$,
$∴b = - 2a$,当$x = - 1$时,$y = a - b + c = 0$,
$∴a - (- 2a)+c = 0$,即$3a + c = 0$,$∴c = - 3a$,
$∴a - c = a - (- 3a)=4a>0$,故①正确;
$∵$图象开口向上,对称轴为直线$x = 1$,
$∴$当$x = 1$时,函数有最小值,最小值在$x$轴的下方,
$∴$抛物线$y = ax²+bx + c$与直线$y = 5$有两个不同的交点,$∴$方程$ax²+bx + c - 5 = 0$有两个不相等的实数根,故②错误;
$∵$二次函数$y = ax²+bx + c$与$y$轴交于点$C(0,m)$,其中$- 4<m< - 3$,$∴$当$x = 0$,$y = c = m$,$∴ - 4<c< - 3$。$∵c = - 3a$,$b = - 2a$,$c = \frac{3}{2}b$,
$∴ - 4<\frac{3}{2}b< - 3$,解得$-\frac{8}{3}<b< - 2$,故③正确;
当$x = 1$时,函数有最小值,最小值为$y = a + b + c<0$,$b = - 2a$,$∴b - a = - 2a - a = - 3a<0$,
$∴\frac{a + b + c}{b - a}>0$,故④正确。
综上所述,正确的有①③④,错误的有②,
$∴$错误的有$1$个。故选A。
$∴$对称轴为直线$x = 1$,$a>0$,
$∴b = - 2a$,当$x = - 1$时,$y = a - b + c = 0$,
$∴a - (- 2a)+c = 0$,即$3a + c = 0$,$∴c = - 3a$,
$∴a - c = a - (- 3a)=4a>0$,故①正确;
$∵$图象开口向上,对称轴为直线$x = 1$,
$∴$当$x = 1$时,函数有最小值,最小值在$x$轴的下方,
$∴$抛物线$y = ax²+bx + c$与直线$y = 5$有两个不同的交点,$∴$方程$ax²+bx + c - 5 = 0$有两个不相等的实数根,故②错误;
$∵$二次函数$y = ax²+bx + c$与$y$轴交于点$C(0,m)$,其中$- 4<m< - 3$,$∴$当$x = 0$,$y = c = m$,$∴ - 4<c< - 3$。$∵c = - 3a$,$b = - 2a$,$c = \frac{3}{2}b$,
$∴ - 4<\frac{3}{2}b< - 3$,解得$-\frac{8}{3}<b< - 2$,故③正确;
当$x = 1$时,函数有最小值,最小值为$y = a + b + c<0$,$b = - 2a$,$∴b - a = - 2a - a = - 3a<0$,
$∴\frac{a + b + c}{b - a}>0$,故④正确。
综上所述,正确的有①③④,错误的有②,
$∴$错误的有$1$个。故选A。
5. (广安中考)如图,二次函数$y=ax^{2}+bx+c$($a,b,c$为常数,$a\neq 0$)的图象交$x$轴于$A,B$两点,点$A$的坐标是$(-1,0)$,点$B$的坐标是$(n,0)$,有下列结论:
①$abc< 0$;
②$4a+c>2b$;
③关于$x$的方程$ax^{2}+bx+c=0$的解是$x_{1}=-1$,$x_{2}=n$;
④$-\dfrac{b}{2a}=\dfrac{n-1}{2}$.
其中正确的有(
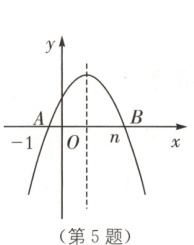
A.$1$个
B.$2$个
C.$3$个
D.$4$个
①$abc< 0$;
②$4a+c>2b$;
③关于$x$的方程$ax^{2}+bx+c=0$的解是$x_{1}=-1$,$x_{2}=n$;
④$-\dfrac{b}{2a}=\dfrac{n-1}{2}$.
其中正确的有(
C
).
A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
5.C[解析]根据图象,可得抛物线的开口向下,交$y$轴于正半轴,$∴a<0$,$c>0$。
又抛物线的对称轴在$y$轴右侧,$x = -\frac{b}{2a}>0$,
$∴b>0$,$∴abc<0$,故结论①正确;
由函数的图象,可得当$x = - 2$时,$y<0$,即$4a - 2b + c<0$,故结论②错误;
$∵$二次函数$y = ax²+bx + c$的图象交$x$轴于$A$,$B$两点,点$A(- 1,0)$,点$B(n,0)$,
$∴$关于$x$的方程$ax²+bx + c = 0$的解是$x₁ = - 1$,$x₂ = n$,$-\frac{b}{2a}=\frac{-1 + n}{2}$,故结论③④正确。
综上,结论正确的有$3$个。故选C。
又抛物线的对称轴在$y$轴右侧,$x = -\frac{b}{2a}>0$,
$∴b>0$,$∴abc<0$,故结论①正确;
由函数的图象,可得当$x = - 2$时,$y<0$,即$4a - 2b + c<0$,故结论②错误;
$∵$二次函数$y = ax²+bx + c$的图象交$x$轴于$A$,$B$两点,点$A(- 1,0)$,点$B(n,0)$,
$∴$关于$x$的方程$ax²+bx + c = 0$的解是$x₁ = - 1$,$x₂ = n$,$-\frac{b}{2a}=\frac{-1 + n}{2}$,故结论③④正确。
综上,结论正确的有$3$个。故选C。
查看更多完整答案,请扫码查看


