《2025年实验班中考数学压轴题》

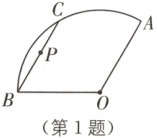
1.(沧州二模)如图，在扇形$OBA$中，点$C$在弧$AB$上，连接$BC$，$P$为$BC$的中点.若$OA = 6$，$\angle AOB = 120°$，则点$C$沿弧从点$B$运动到点$A$的过程中，点$P$所经过的路径长为(B).

A.$4\pi$
B.$2\pi$
C.$3\sqrt{3}$
D.$6$

答案：
1. B　[解析]如图，连接OP,AB,过点O作OD⊥AB于点D,取OB的中点E,连接DE，则∠BOD=∠AOD=60°,BE=3.
∵P是BC的中点，
∴OP⊥BC,
∴点P在以OB为直径的⊙E上.
　　　　　　　　　　　　　　　　
由题意知，点P运动的路径为BD.
∵ED=EO,∠BOD=60°,
∴△ODE为等边三角形，
∴∠OED=60°.
∴∠BED=120°,
∴点P所经过的路径长为BD=$\frac{120\pi · 3}{180}$=2π.故选B.

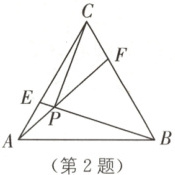
2.(武汉二中广雅中学模拟)如图，在边长为$12$的等边三角形$ABC$中，点$E$在边$AC$上自$A$向$C$运动，点$F$在边$CB$上自$C$向$B$运动，且运动速度相同，连接$BE$，$AF$交于点$P$，连接$CP$，在运动过程中，点$P$的运动路径长为(D).

A.$\frac{9}{2}\pi$
B.$4\sqrt{3} - \frac{3}{4}\pi$
C.$8\sqrt{3} - \frac{3}{2}\pi$
D.$\frac{8\sqrt{3}}{3}\pi$

答案：
2. D　[解析]如图，过点A作OA⊥AC于点A，过点B作OB⊥BC于点B，连接OC,交AB于点D.
∵△ACB是等边三角形，
　　　　　　　　　　　　　　　　
∴AC=BC=AB,∠ACB=∠CAB=60°,
∴∠AOB=360°−60°−90°−90°=120°.
∵OC=OC,
∴Rt△ACO≌Rt△BCO(HL),
∴OA=OB,
∴OC是AB的垂直平分线，AD=BD=$\frac{1}{2}$AB=6.在Rt△ADO中,∠DAO=30°,
∴OD=2$\sqrt{3}$,OA=2OD=4$\sqrt{3}$.
∵AE=CF,
∴△ACF≌△BAE(SAS),
∴∠CAF=∠ABE.
∵∠CAF+∠BAP=60°,
∴∠ABE+∠BAP=60°,
∴∠APB=180°−60°=120°,
∴点P的运动路径是以点O为圆心，以OA为半径的弧AB，$l_{AB}$=2π×4$\sqrt{3}$×$\frac{120}{360}$=$\frac{8\sqrt{3}\pi}{3}$.故选D.

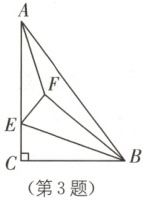
3.(云浮罗定区三模)如图，在$Rt\triangle ABC$中，$\angle ACB = 90°$，$E$为$AC$边上的任意一点，把$\triangle BCE$沿$BE$折叠，得到$\triangle BFE$，连接$AF$.若$BC = 6$，$AC = 8$，则$AF$的最小值为4.

答案：
3. 4　[解析]
∵△BCE沿BE折叠，得到△BFE,
∴BF=BC=6,
∴点F在以B为圆心，6为半径的圆上，如图，设以B为圆心，6为半径的圆与AB交于点F′，
　　　　　　　
则BF′=BC=6,AF的最小值为AF′的长.在Rt△ABC中,BC=6,AC=8,
∴AB=$\sqrt{BC^{2}+AC^{2}}$=$\sqrt{6^{2}+8^{2}}$=10,
∴AF′=AB−BF′=10−6=4,
∴AF的最小值为4.

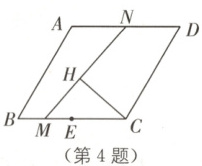
4.(扬州梅岭中学三模)如图，菱形$ABCD$的边长为$12$，$\angle B = 60°$，$E$为边$BC$的中点.点$M$从点$E$出发，以每秒$1$个单位长度的速度向点$B$运动，点$N$同时从点$A$出发，以每秒$2$个单位长度的速度向点$D$运动，连接$MN$，过点$C$作$CH \perp MN$于点$H$.当点$M$到达点$B$时，点$N$也停止运动，则点$H$的运动路径长是(D).

A.$6$
B.$12$
C.$\frac{2\sqrt{3}}{3}\pi$
D.$\frac{4\sqrt{3}}{3}\pi$

答案：
4. D　[解析]如图，连接AE,AC,BD,设AC,BD交于点P，AE交MN于点F,连接CF，设CF的中点为O,连接OP,OE.
　　　　　　　
∵菱形ABCD的边长为12,∠B=60°，
∴AB=BC=12,△ABC是等边三角形.
∵E为边BC的中点，
∴AE⊥BC,BE=CE=$\frac{1}{2}$BC=6,AE=6$\sqrt{3}$.
∵点M的速度为每秒1个单位长度，点N的速度为每秒2个单位长度，
∴$\frac{ME}{AN}$=$\frac{1}{2}$.
∵AN//ME,
∴△ANF∽△EMF,
∴$\frac{EF}{AF}$=$\frac{EM}{AN}$=$\frac{1}{2}$,
∴FE=$\frac{1}{3}$AE=2$\sqrt{3}$,CF=$\sqrt{FE^{2}+CE^{2}}$=4$\sqrt{3}$,
∴MN必经过点F.
∵CH⊥MN,AE⊥BC,
∴点H在以CF为直径的圆上，且F,E,C,H四点共圆.
∵当点M到达点B时，点N到达点D，AC⊥BD，
∴点H的运动路径长是$\widehat{EP}$的长.
∵∠BCA=60°,
∴∠EOP=2∠BCA=120°,
∴$\widehat{EP}$=$\frac{120\pi×2\sqrt{3}}{180}$=$\frac{4\sqrt{3}\pi}{3}$，即点H的运动路径长是$\frac{4\sqrt{3}}{3}\pi$.故选D.

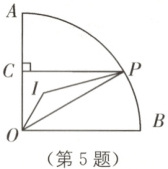
5.(宁波模拟)如图，在扇形$OAB$中，$OA = 4$，$\angle AOB = 90°$，$P$是$\overset{\frown}{AB}$上的动点，过点$P$作$PC \perp OA$于点$C$.设$\triangle OPC$的内心为$I$，连接$OI$，$PI$，当点$P$从点$B$运动到点$A$时，内心$I$所经过的路径长为$\sqrt{2}\pi$.

答案：
5.　$\sqrt{2}\pi$ [解析]如图，连接AI.

∵点I是△OPC的内心，
∴∠IOP=$\frac{1}{2}$∠COP,∠IPO=$\frac{1}{2}$∠CPO,
∴∠IOP+∠IPO=$\frac{1}{2}$(∠COP+∠CPO).
∵PC⊥OA,
∴∠PCO=90°,
∴∠COP+∠CPO=90°,
∴∠IOP+∠IPO=$\frac{1}{2}$×90°=45°,
∴∠OIP=180°−45°=135°.
∵OI平分∠COP,
∴∠COI=∠POI.
∵OA=OP,OI=OI,
∴△AOI≌△POI(SAS),
∴∠AIO=∠PIO=135°,
∴当点P从点B运动到点A时,内心I所经过的路径长为图中的$\widehat{OA}$的长度，设△AOI的外接圆为⊙O,连接AM,OM,在优弧ANO上任取一点N,连接AN,ON,则∠N=45°,
∴∠M=90°,
∴AM=OM=$\frac{\sqrt{2}}{2}$AO=2$\sqrt{2}$,
∴$\widehat{OA}$的长=$\frac{90\pi×2\sqrt{2}}{180}$=$\sqrt{2}\pi$.

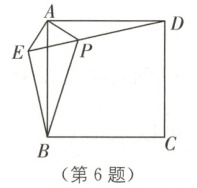
6.(广州番禺区二模)如图，在正方形$ABCD$中，$AB = 2$，$E$是平面内一点，$\angle AED = 45°$，连接$DE$.过点$A$作$AE$的垂线交直线$DE$于点$P$，连接$BP$.下列结论：①$\triangle APD \cong \triangle AEB$；②$EB \perp ED$；③当$\angle ADE = 30°$时，$AE = \sqrt{3}$；④$CP$的最小值为$\sqrt{10} - \sqrt{2}$.其中正确的结论是①②④.
答案见$P20$

答案： 6.①②④　[解析]
∵AE⊥AP,
∴∠EAP=90°.
∵∠AED=45°,
∴△AEP是等腰直角三角形,
∴AE=AP、∠APE=∠AEP=45°,
∴∠APD=180°−∠APE=135°.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE=∠DAP=90°−∠BAP,
∴△BAE≌△DAP(SAS),故①正确;
∴∠BEA=∠DPA=135°,
∴∠BED=∠BEA−∠AED=90°,即EB⊥ED,故②正确;
　如图，过点A作AH⊥DE.当∠ADE=30°时,则AH=$\frac{1}{2}$AD=1,
∴AE=$\sqrt{2}$AH=$\sqrt{2}$,故③错误;作△APD的外接圆，设该外接圆的圆心为O，在优弧AD上取一点G，连接OA,OD,AG,DG，
∴∠AGD=180°−∠APD=45°,
∴∠AOD=2∠AGD=90°.
∵OA=OD,
∴∠OAD=∠ODA=45°,
∴OD=AD·sin∠OAD=$\sqrt{2}$.过点O作OT⊥CD交CD延长线于点T，连接OP，CP，OC，
∴∠ODT=∠ADT−∠ODA=45°,
∴OT=OD·sin∠ODT=1，DT=OD·cos∠ODT=1，
∴CT=CD+DT=3，
∴OC=$\sqrt{OT^{2}+CT^{2}}$=$\sqrt{10}$.
∵CP≥OC-OP，
∴当点P在线段OC上时，CP有最小值，最小值为OC-OP的值，即最小值为$\sqrt{10}$-$\sqrt{2}$，故④正确.综上所述，正确的有①②④.