2025年实验班中考数学压轴题
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班中考数学压轴题 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
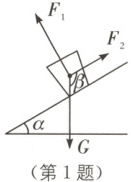
1. (盐城阜宁一模)一只杯子静止在斜面上,其受力分析如图所示,重力$G$的方向竖直向下,支持力$F_1$的方向与斜面垂直,摩擦力$F_2$的方向与斜面平行。若斜面的坡角$\alpha = 30°$,则摩擦力$F_2$与重力$G$方向的夹角$\beta$的度数为($\quad$)。
A.$125°$
B.$120°$
C.$115°$
D.$60°$
(第3题)

A.$125°$
B.$120°$
C.$115°$
D.$60°$
(第3题)
答案:
1.B [解析]根据受力分析图,可知∠FAB=90°,
∴∠BFA+∠ABF=90°.
∵α=30°,
∴∠FBA=60°,
∴∠CBD=60°.
∵CE//DF,
∴β+∠CBD=180°,
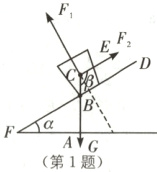
∴β=120°.故选B.
1.B [解析]根据受力分析图,可知∠FAB=90°,
∴∠BFA+∠ABF=90°.
∵α=30°,
∴∠FBA=60°,
∴∠CBD=60°.
∵CE//DF,
∴β+∠CBD=180°,

∴β=120°.故选B.
2. 传统文化 罗士琳法则 (扬州中考)清代扬州数学家罗士琳痴迷于勾股定理的研究,提出了推算勾股数的“罗士琳法则”。法则的提出,不仅简化了勾股数的生成过程,也体现了中国传统数学在数论领域的贡献。由此法则写出了下列几组勾股数:①$3$,$4$,$5$;②$5$,$12$,$13$;③$7$,$24$,$25$;④$9$,$40$,$41$;$·s$。根据上述规律,写出第⑤组勾股数为。
答案:
2.11,60,61 [解析]通过观察得第①组勾股数分别为$2×1 + 1=3$,$2×1^2+2×1=4$,$2×1^2+2×1 + 1=5$;第②组勾股数分别为$2×2 + 1=5$,$2×2^2+2×2=12$,$2×2^2+2×2 + 1=13$;第③组勾股数分别为$2×3 + 1=7$,$2×3^2+2×3=24$,$2×3^2+2×3 + 1=25$;第④组勾股数为$2×4 + 1=9$,$2×4^2+2×4=40$,$2×4^2+2×4 + 1=41$,所以第⑤组勾股数为$2×5 + 1=11$,$2×5^2+2×5=60$,$2×5^2+2×5 + 1=61$.
question:2. 传统文化 罗士琳法则 (扬州中考)清代扬州数学家罗士琳痴迷于勾股定理的研究,提出了推算勾股数的“罗士琳法则”。法则的提出,不仅简化了勾股数的生成过程,也体现了中国传统数学在数论领域的贡献。由此法则写出了下列几组勾股数:①$3$,$4$,$5$;②$5$,$12$,$13$;③$7$,$24$,$25$;④$9$,$40$,$41$;$·s$。根据上述规律,写出第⑤组勾股数为
question:2. 传统文化 罗士琳法则 (扬州中考)清代扬州数学家罗士琳痴迷于勾股定理的研究,提出了推算勾股数的“罗士琳法则”。法则的提出,不仅简化了勾股数的生成过程,也体现了中国传统数学在数论领域的贡献。由此法则写出了下列几组勾股数:①$3$,$4$,$5$;②$5$,$12$,$13$;③$7$,$24$,$25$;④$9$,$40$,$41$;$·s$。根据上述规律,写出第⑤组勾股数为
11,60,61
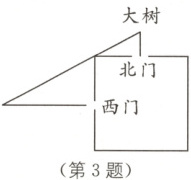
。 3. 传统文化 《九章算术》 (泰州泰兴西城中学三模)小明对《九章算术》中的“表望方城”问题进行了改编:如图,一座正方形城堡在正北和正西城墙的正中间各开一门,出北门$100$步有一棵大树,出西门$225$步后刚好看到北门外的这棵大树,则该城堡的边长为步。

答案:
3.300 [解析]如图,设该城堡的边长为x步,则$BE=BC=\frac{1}{2}x$步.由题意,得$DE=100$步,$AC=225$步.
∵BE//AC,
∴∠DBE=∠BAC.
∵∠DEB=∠BCA=90°,
∴△DBE∽△BAC,
∴$DE:BC=BE:AC$,
∴$100:\frac{1}{2}x=\frac{1}{2}x:225$,
∴$x=300$(舍去负值),
∴该城堡的边长因为边长是正数,所以要舍去负根为300步.

question:3. 传统文化 《九章算术》 (泰州泰兴西城中学三模)小明对《九章算术》中的“表望方城”问题进行了改编:如图,一座正方形城堡在正北和正西城墙的正中间各开一门,出北门$100$步有一棵大树,出西门$225$步后刚好看到北门外的这棵大树,则该城堡的边长为

3.300 [解析]如图,设该城堡的边长为x步,则$BE=BC=\frac{1}{2}x$步.由题意,得$DE=100$步,$AC=225$步.
∵BE//AC,
∴∠DBE=∠BAC.
∵∠DEB=∠BCA=90°,
∴△DBE∽△BAC,
∴$DE:BC=BE:AC$,
∴$100:\frac{1}{2}x=\frac{1}{2}x:225$,
∴$x=300$(舍去负值),
∴该城堡的边长因为边长是正数,所以要舍去负根为300步.

question:3. 传统文化 《九章算术》 (泰州泰兴西城中学三模)小明对《九章算术》中的“表望方城”问题进行了改编:如图,一座正方形城堡在正北和正西城墙的正中间各开一门,出北门$100$步有一棵大树,出西门$225$步后刚好看到北门外的这棵大树,则该城堡的边长为
300
步。
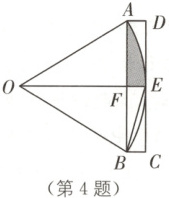
4. 传统文化 割圆术 (河南中考)我国魏晋时期数学家刘徽在为《九章算术》作注时,创立了“割圆术”。如图是研究“割圆术”时的一个图形,$\overset{\frown}{AB}$所在圆的圆心为点$O$,四边形$ABCD$为矩形,边$CD$与$\odot O$相切于点$E$,连接$BE$,$\angle ABE = 15°$,连接$OE$交$AB$于点$F$。
若$AB = 4$,则图中阴影部分的面积为。
若$AB = 4$,则图中阴影部分的面积为。

答案:
4.$\frac{4\pi}{3}-2\sqrt{3}$ [解析]
∵边CD与⊙O相切于点E,
∴OE⊥CD.
∵四边形ABCD为矩形,
∴AB//CD,
∴OE⊥AB,
∴$AF=FB=\frac{1}{2}AB=\frac{1}{2}×4=2$.由圆周角定理,得∠AOE=2∠ABE=30°,
∴$OA=2AF=4$.在Rt△OAF中,由勾股定理,得$OF=\sqrt{OA^2 - AF^2}=\sqrt{4^2 - 2^2}=2\sqrt{3}$,则$S_{阴影部分}=S_{扇形AOE}-S_{△AOF}=\frac{30\pi×4^2}{360}-\frac{1}{2}×2×2\sqrt{3}=\frac{4\pi}{3}-2\sqrt{3}$.
question:4. 传统文化 割圆术 (河南中考)我国魏晋时期数学家刘徽在为《九章算术》作注时,创立了“割圆术”。如图是研究“割圆术”时的一个图形,$\overset{\frown}{AB}$所在圆的圆心为点$O$,四边形$ABCD$为矩形,边$CD$与$\odot O$相切于点$E$,连接$BE$,$\angle ABE = 15°$,连接$OE$交$AB$于点$F$。
若$AB = 4$,则图中阴影部分的面积为

4.$\frac{4\pi}{3}-2\sqrt{3}$ [解析]
∵边CD与⊙O相切于点E,
∴OE⊥CD.
∵四边形ABCD为矩形,
∴AB//CD,
∴OE⊥AB,
∴$AF=FB=\frac{1}{2}AB=\frac{1}{2}×4=2$.由圆周角定理,得∠AOE=2∠ABE=30°,
∴$OA=2AF=4$.在Rt△OAF中,由勾股定理,得$OF=\sqrt{OA^2 - AF^2}=\sqrt{4^2 - 2^2}=2\sqrt{3}$,则$S_{阴影部分}=S_{扇形AOE}-S_{△AOF}=\frac{30\pi×4^2}{360}-\frac{1}{2}×2×2\sqrt{3}=\frac{4\pi}{3}-2\sqrt{3}$.
question:4. 传统文化 割圆术 (河南中考)我国魏晋时期数学家刘徽在为《九章算术》作注时,创立了“割圆术”。如图是研究“割圆术”时的一个图形,$\overset{\frown}{AB}$所在圆的圆心为点$O$,四边形$ABCD$为矩形,边$CD$与$\odot O$相切于点$E$,连接$BE$,$\angle ABE = 15°$,连接$OE$交$AB$于点$F$。
若$AB = 4$,则图中阴影部分的面积为
$\frac{4\pi}{3}-2\sqrt{3}$
。
5. 跨学科 自由落体 (南通海门区二模)如果把小球从地面以$10\ m/s$的速度竖直上抛,则小球离地面的高度$h$(单位:$m$)与经过的时间$x$(单位:$s$)的关系式为$h = 10x - 4.9x^2$。根据该物理规律,下列对方程$10x - 4.9x^2 = 5$的两根$x_1 \approx 0.88$,$x_2 \approx 1.16$的解释正确的是($\quad$)。
A.小球两次到达离地面的高度为$5\ m$的位置,其时间间隔约为$0.28\ s$
B.小球经过的时间约$1.16\ s$离地面的高度为$5\ m$,并将继续上升
C.小球离地面的高度为$5\ m$时,经过的时间约为$0.88\ s$
D.小球经过的时间约$1.02\ s$离地面的高度为$5\ m$
A.小球两次到达离地面的高度为$5\ m$的位置,其时间间隔约为$0.28\ s$
B.小球经过的时间约$1.16\ s$离地面的高度为$5\ m$,并将继续上升
C.小球离地面的高度为$5\ m$时,经过的时间约为$0.88\ s$
D.小球经过的时间约$1.02\ s$离地面的高度为$5\ m$
答案:
5.A [解析]方程$10x - 4.9x^2=5$的两根$x_1\approx0.88$,$x_2\approx1.16$分别表示的是上升0.88s时,距离地面为5m,且继续上升;下降过程中,1.16s时,距离地面为5m,且继续下降,两次距离地面5m的时间间隔为$1.16 - 0.88=0.28$(s),故A正确,符合题意.故选A.
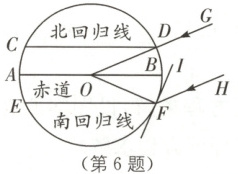
6. (北京中考)如图,$\odot O$是地球的示意图,其中$AB$表示赤道,$CD$,$EF$分别表示北回归线和南回归线,$\angle DOB = \angle FOB = 23.5°$。夏至日正午时,太阳光线$GD$所在直线经过地心$O$,此时点$F$处的太阳高度角$\angle IFH$(即平行于$GD$的光线$HF$与$\odot O$的切线$FI$所成的锐角)的大小为$$$°$。
答案见$P41$
答案见$P41$

答案:
6.43 [解析]
∵∠DOB=∠FOB=23.5°,
∴∠DOF=∠DOB+∠FOB=47°.
∵GD//HF,
∴∠OFH=180° - ∠DOF=180° - 47°=133°.
∵FI是⊙O的切线,
∴OF⊥FI,
∴∠OFI=90°,
∴∠IFH=133° - 90°=43°.
question:6. (北京中考)如图,$\odot O$是地球的示意图,其中$AB$表示赤道,$CD$,$EF$分别表示北回归线和南回归线,$\angle DOB = \angle FOB = 23.5°$。夏至日正午时,太阳光线$GD$所在直线经过地心$O$,此时点$F$处的太阳高度角$\angle IFH$(即平行于$GD$的光线$HF$与$\odot O$的切线$FI$所成的锐角)的大小为$$
答案见$P41$

6.43 [解析]
∵∠DOB=∠FOB=23.5°,
∴∠DOF=∠DOB+∠FOB=47°.
∵GD//HF,
∴∠OFH=180° - ∠DOF=180° - 47°=133°.
∵FI是⊙O的切线,
∴OF⊥FI,
∴∠OFI=90°,
∴∠IFH=133° - 90°=43°.
question:6. (北京中考)如图,$\odot O$是地球的示意图,其中$AB$表示赤道,$CD$,$EF$分别表示北回归线和南回归线,$\angle DOB = \angle FOB = 23.5°$。夏至日正午时,太阳光线$GD$所在直线经过地心$O$,此时点$F$处的太阳高度角$\angle IFH$(即平行于$GD$的光线$HF$与$\odot O$的切线$FI$所成的锐角)的大小为$$
43
$°$。答案见$P41$

查看更多完整答案,请扫码查看


