2025年实验班中考数学压轴题
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班中考数学压轴题 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
1. (天津中考)如图,在$ \triangle ABC $中,$ \angle ACB = 90° $,将$ \triangle ABC $绕点$ A $顺时针旋转得到$ \triangle AB'C' $,点$ B $,$ C $的对应点分别为$ B' $,$ C' $,$ B'C' $的延长线与边$ BC $相交于点$ D $,连接$ CC' $。若$ AC = 4 $,$ CD = 3 $,则线段$ CC' $的长为(
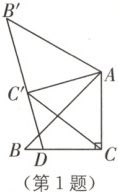
A.$ \dfrac{12}{5} $
B.$ \dfrac{16}{5} $
C.$ 4 $
D.$ \dfrac{24}{5} $
D
)。
A.$ \dfrac{12}{5} $
B.$ \dfrac{16}{5} $
C.$ 4 $
D.$ \dfrac{24}{5} $
答案:
1. D [解析]如图,连接AD,交CC'于点O.

由旋转,得AC' = AC = 4,∠AC'B' = ∠ACB = 90°,
∴∠AC'D = 90°.
在Rt△ACD和Rt△AC'D中,$\left\{ \begin{array}{l} AD = AD, \\ AC = AC', \end{array} \right.$
∴Rt△ACD≌Rt△AC'D(HL),
∴C'D = CD = 3,
∴AD垂直平分CC',
∴CC' = 2OC,AD⊥CC'.
∵∠ACB = 90°,AC = 4,CD = 3,
∴AD = $\sqrt{AC^{2} + CD^{2}}$ = 5.
∵$S_{\triangle ACD}$ = $\frac{1}{2}$CD·AC = $\frac{1}{2}$AD·OC,
∴OC = $\frac{CD·AC}{AD}$ = $\frac{3×4}{5}$ = $\frac{12}{5}$,
∴CC' = 2×$\frac{12}{5}$ = $\frac{24}{5}$. 故选D.
1. D [解析]如图,连接AD,交CC'于点O.

由旋转,得AC' = AC = 4,∠AC'B' = ∠ACB = 90°,
∴∠AC'D = 90°.
在Rt△ACD和Rt△AC'D中,$\left\{ \begin{array}{l} AD = AD, \\ AC = AC', \end{array} \right.$
∴Rt△ACD≌Rt△AC'D(HL),
∴C'D = CD = 3,
∴AD垂直平分CC',
∴CC' = 2OC,AD⊥CC'.
∵∠ACB = 90°,AC = 4,CD = 3,
∴AD = $\sqrt{AC^{2} + CD^{2}}$ = 5.
∵$S_{\triangle ACD}$ = $\frac{1}{2}$CD·AC = $\frac{1}{2}$AD·OC,
∴OC = $\frac{CD·AC}{AD}$ = $\frac{3×4}{5}$ = $\frac{12}{5}$,
∴CC' = 2×$\frac{12}{5}$ = $\frac{24}{5}$. 故选D.
2. (无锡锡山区一模)如图,在矩形$ ABCD $中,$ AB = 6 $,$ BC = 8 $,$ P $是对角线$ AC $上的动点,连接$ DP $,将直线$ DP $绕点$ P $顺时针旋转使$ \angle DPG = \angle DAC $,且过点$ D $作$ DG \perp PG $,连接$ CG $,则$ CG $最小值为(
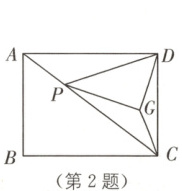
A.$ \dfrac{12}{5} $
B.$ \dfrac{14}{5} $
C.$ \dfrac{72}{25} $
D.$ \dfrac{36}{25} $
C
)。
A.$ \dfrac{12}{5} $
B.$ \dfrac{14}{5} $
C.$ \dfrac{72}{25} $
D.$ \dfrac{36}{25} $
答案:
2. C [解析]如图,过点D作DH⊥AC于点H,连接HG并延长交CD于点E,过点H作HF⊥CD于点F.

∵DG⊥PG,DH⊥AC,
∴∠DGP = ∠DHA = 90°.
∵∠DPG = ∠DAC,
∴△DPG∽△DAH,
∴$\frac{DP}{DG}$ = $\frac{DA}{DH}$,∠PDG = ∠ADH,
∴∠ADP = ∠HDG,
∴△ADP∽△HDG,
∴∠DAP = ∠DHG为定值,
∴点G在HE上运动,当CG⊥HE时,CG取得最小值.
∵∠ADC = 90°,DH⊥AC,
∴△ADH∽△DCH,
∴∠DAH = ∠CDH,
∴∠DHG = ∠CDH,
∴HE = DE.
∵∠DHG + ∠EHC = 90°,∠HCD + ∠CDH = 90°,
∴∠EHC = ∠HCD,
∴HE = CE,
∴HE = DE = CE = $\frac{1}{2}$CD = 3.
∵四边形ABCD为矩形,∠ADC = 90°,CD = AB = 6,
BC = AD = 8,
∴AC = $\sqrt{AD^{2} + CD^{2}}$ = 10.
∵$S_{\triangle ADC}$ = $\frac{1}{2}$AD·CD = $\frac{1}{2}$AC·DH,
∴DH = $\frac{AD·CD}{AC}$ = $\frac{24}{5}$,
∴AH = $\sqrt{AD^{2} - DH^{2}}$ = $\frac{32}{5}$,
∴CH = AC - AH = $\frac{18}{5}$.
∵HF⊥CD,AD⊥CD,
∴HF//AD,
∴△CHF∽△CAD,
∴$\frac{CH}{CA}$ = $\frac{HF}{AD}$,
∴$\frac{\frac{18}{5}}{10}$ = $\frac{HF}{8}$,
∴HF = $\frac{72}{25}$.
∵CG⊥HE,HF⊥CE,
∴$S_{\triangle CHE}$ = $\frac{1}{2}$HE·CG = $\frac{1}{2}$CE·HF,
∴CG = $\frac{CE·HF}{HE}$ = $\frac{3×\frac{72}{25}}{3}$ = $\frac{72}{25}$. 故选C.
2. C [解析]如图,过点D作DH⊥AC于点H,连接HG并延长交CD于点E,过点H作HF⊥CD于点F.

∵DG⊥PG,DH⊥AC,
∴∠DGP = ∠DHA = 90°.
∵∠DPG = ∠DAC,
∴△DPG∽△DAH,
∴$\frac{DP}{DG}$ = $\frac{DA}{DH}$,∠PDG = ∠ADH,
∴∠ADP = ∠HDG,
∴△ADP∽△HDG,
∴∠DAP = ∠DHG为定值,
∴点G在HE上运动,当CG⊥HE时,CG取得最小值.
∵∠ADC = 90°,DH⊥AC,
∴△ADH∽△DCH,
∴∠DAH = ∠CDH,
∴∠DHG = ∠CDH,
∴HE = DE.
∵∠DHG + ∠EHC = 90°,∠HCD + ∠CDH = 90°,
∴∠EHC = ∠HCD,
∴HE = CE,
∴HE = DE = CE = $\frac{1}{2}$CD = 3.
∵四边形ABCD为矩形,∠ADC = 90°,CD = AB = 6,
BC = AD = 8,
∴AC = $\sqrt{AD^{2} + CD^{2}}$ = 10.
∵$S_{\triangle ADC}$ = $\frac{1}{2}$AD·CD = $\frac{1}{2}$AC·DH,
∴DH = $\frac{AD·CD}{AC}$ = $\frac{24}{5}$,
∴AH = $\sqrt{AD^{2} - DH^{2}}$ = $\frac{32}{5}$,
∴CH = AC - AH = $\frac{18}{5}$.
∵HF⊥CD,AD⊥CD,
∴HF//AD,
∴△CHF∽△CAD,
∴$\frac{CH}{CA}$ = $\frac{HF}{AD}$,
∴$\frac{\frac{18}{5}}{10}$ = $\frac{HF}{8}$,
∴HF = $\frac{72}{25}$.
∵CG⊥HE,HF⊥CE,
∴$S_{\triangle CHE}$ = $\frac{1}{2}$HE·CG = $\frac{1}{2}$CE·HF,
∴CG = $\frac{CE·HF}{HE}$ = $\frac{3×\frac{72}{25}}{3}$ = $\frac{72}{25}$. 故选C.
3. (苏州工业园区一模)如图,在$ \triangle ABC $中,$ \angle BAC = 64° $,$ \angle C = 36° $。将$ \triangle ABC $绕点$ A $按逆时针方向旋转后得$ \triangle ADE $,$ AE $与$ BD $相交于点$ F $。当$ DE // AB $时,$ \angle AFD = $
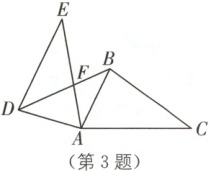
76或14
$° $。
答案:
3. 76或14 [解析]如图
(1),

在△ABC中,∠BAC = 64°,∠C = 36°,
∴∠ABC = 180° - 64° - 36° = 80°,
∴∠ADE = ∠ABC = 80°.
∵AB//DE,
∴∠BAD + ∠ADE = 180°,
∴∠BAD = 100°.
∵AD = AB,
∴∠ADF = 40°.
∵∠EAD = ∠CAB = 64°,
∴∠AFD = 180° - 40° - 64° = 76°;
如图
(2),
∵AB//DE,
∴∠BAD = ∠ADE = 80°.
∵AD = AB,
∴∠ADF = ∠ABD = 50°,
∴∠EDF = ∠ADE + ∠ADF = 80° + 50° = 130°.
∵∠E = 36°,
∴∠AFD = 180° - 36° - 130° = 14°.
综上所述,∠AFD = 76°或14°.
3. 76或14 [解析]如图
(1),

在△ABC中,∠BAC = 64°,∠C = 36°,
∴∠ABC = 180° - 64° - 36° = 80°,
∴∠ADE = ∠ABC = 80°.
∵AB//DE,
∴∠BAD + ∠ADE = 180°,
∴∠BAD = 100°.
∵AD = AB,
∴∠ADF = 40°.
∵∠EAD = ∠CAB = 64°,
∴∠AFD = 180° - 40° - 64° = 76°;
如图
(2),
∵AB//DE,
∴∠BAD = ∠ADE = 80°.
∵AD = AB,
∴∠ADF = ∠ABD = 50°,
∴∠EDF = ∠ADE + ∠ADF = 80° + 50° = 130°.
∵∠E = 36°,
∴∠AFD = 180° - 36° - 130° = 14°.
综上所述,∠AFD = 76°或14°.
4. 如图,菱形$ ABCD $边长为$ 4 $,$ \angle ABC = 120° $,点$ E $在线段$ BC $上,射线$ AE $绕点$ A $逆时针旋转$ 30° $与射线$ BC $交于点$ F $,与线段$ CD $交于点$ G $,且$ DG:GC = 3:1 $,则线段$ EF = $
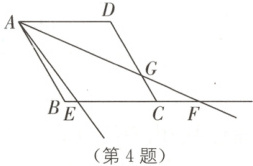
$\frac{74}{15}$
。
答案:
4. $\frac{74}{15}$ [解析]如图,过点G作GH⊥AD于点H,连接AC.

∵四边形ABCD为菱形,∠ABC = 120°,
∴AB = CD = AD = 4,∠ADC = 120°,AC = $4\sqrt{3}$,∠ACB = 30°,AD//BC.
∴$\frac{AD}{CF}$ = $\frac{AG}{GF}$ = $\frac{DG}{CG}$ = 3:1,
∴CF = $\frac{4}{3}$,AG = 3FG.
∵∠CDH = 180° - ∠ADC = 60°,
∴DH = $\frac{1}{2}$DG = $\frac{3}{2}$,
HG = $\sqrt{3}$DH = $\frac{3\sqrt{3}}{2}$,AH = $\frac{11}{2}$,
∴AG = $\sqrt{AH^{2} + GH^{2}}$ = $\sqrt{37}$,
∴AF = $\frac{4}{3}$AG = $\frac{4\sqrt{37}}{3}$.
∵∠EAF = 30°,
∴∠CAE + ∠CAF = 30°.
∵∠CAF + ∠CFA = ∠ACB = 30°,
∴∠CAE = ∠AFE.
∵∠ACE = ∠FAE,
∴△ACE∽△FAE,
∴$\frac{AE}{EF}$ = $\frac{CE}{AE}$ = $\frac{AC}{AF}$ = $\frac{3\sqrt{3}}{\frac{4\sqrt{37}}{3}}$ = $\frac{3\sqrt{3}}{\sqrt{37}}$,
∵CE = EF - CF = EF - $\frac{4}{3}$,
∴$\frac{AE}{EF}$ = $\frac{EF - \frac{4}{3}}{AE}$ = $\frac{3\sqrt{3}}{\sqrt{37}}$,解得EF = $\frac{74}{15}$.
4. $\frac{74}{15}$ [解析]如图,过点G作GH⊥AD于点H,连接AC.

∵四边形ABCD为菱形,∠ABC = 120°,
∴AB = CD = AD = 4,∠ADC = 120°,AC = $4\sqrt{3}$,∠ACB = 30°,AD//BC.
∴$\frac{AD}{CF}$ = $\frac{AG}{GF}$ = $\frac{DG}{CG}$ = 3:1,
∴CF = $\frac{4}{3}$,AG = 3FG.
∵∠CDH = 180° - ∠ADC = 60°,
∴DH = $\frac{1}{2}$DG = $\frac{3}{2}$,
HG = $\sqrt{3}$DH = $\frac{3\sqrt{3}}{2}$,AH = $\frac{11}{2}$,
∴AG = $\sqrt{AH^{2} + GH^{2}}$ = $\sqrt{37}$,
∴AF = $\frac{4}{3}$AG = $\frac{4\sqrt{37}}{3}$.
∵∠EAF = 30°,
∴∠CAE + ∠CAF = 30°.
∵∠CAF + ∠CFA = ∠ACB = 30°,
∴∠CAE = ∠AFE.
∵∠ACE = ∠FAE,
∴△ACE∽△FAE,
∴$\frac{AE}{EF}$ = $\frac{CE}{AE}$ = $\frac{AC}{AF}$ = $\frac{3\sqrt{3}}{\frac{4\sqrt{37}}{3}}$ = $\frac{3\sqrt{3}}{\sqrt{37}}$,
∵CE = EF - CF = EF - $\frac{4}{3}$,
∴$\frac{AE}{EF}$ = $\frac{EF - \frac{4}{3}}{AE}$ = $\frac{3\sqrt{3}}{\sqrt{37}}$,解得EF = $\frac{74}{15}$.
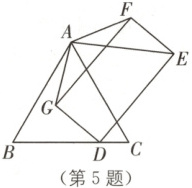
5. 如图,$ \triangle ABC $是等边三角形,矩形$ DEFG $的顶点$ D $在边$ BC $上,且$ BD = 3CD = 3 $,$ DE = AB = 2DG $,连接$ AG $,$ AE $,$ AF $,若将矩形$ DEFG $绕点$ D $旋转一周,当$ AG + AF $最小时,则$ AE $的长度为(
A.$ \sqrt{3} $
B.$ \sqrt{5} $
C.$ 2\sqrt{3} $
D.$ \sqrt{13} $
B
)。
A.$ \sqrt{3} $
B.$ \sqrt{5} $
C.$ 2\sqrt{3} $
D.$ \sqrt{13} $
答案:
5. B [解析]如图,过点A作AH⊥BC于点H,连接AD.

由题意,可得AB = AC = BC,∠B = 60°,
∴BH = CH.
∵BD = 3CD = 3,
∴CD = 1,
∴BC = BD + CD = 3 + 1 = 4,
∴BH = CH = 2,
∴AB = AC = 4,
∴AH = $2\sqrt{3}$.
∵DE = AB = 2DG = 4,
∴DG = 2.
∵四边形DEFG是矩形,
∴FG = DE = 4,∠DGF = 90°,EF = DG = 2.
∵AG + AF ≥ 4.
∵仅当A,G,F三点共线时,AG + AF取得最小值为4.
∵DH = CH - CD = 2 - 1 = 1,
∴AD = $\sqrt{AH^{2} + DH^{2}}$ = $\sqrt{(2\sqrt{3})^{2} + 1^{2}}$ = $\sqrt{13}$,AG = $\sqrt{AD^{2} - DG^{2}}$ = $\sqrt{(\sqrt{13})^{2} - 2^{2}}$ = 3,
∴AF = GF - AG = 4 - 3 = 1,AE = $\sqrt{AF^{2} + EF^{2}}$ = $\sqrt{1^{2} + 2^{2}}$ = $\sqrt{5}$,
∴当AG + AF最小时,AE = $\sqrt{5}$. 故选B.
5. B [解析]如图,过点A作AH⊥BC于点H,连接AD.

由题意,可得AB = AC = BC,∠B = 60°,
∴BH = CH.
∵BD = 3CD = 3,
∴CD = 1,
∴BC = BD + CD = 3 + 1 = 4,
∴BH = CH = 2,
∴AB = AC = 4,
∴AH = $2\sqrt{3}$.
∵DE = AB = 2DG = 4,
∴DG = 2.
∵四边形DEFG是矩形,
∴FG = DE = 4,∠DGF = 90°,EF = DG = 2.
∵AG + AF ≥ 4.
∵仅当A,G,F三点共线时,AG + AF取得最小值为4.
∵DH = CH - CD = 2 - 1 = 1,
∴AD = $\sqrt{AH^{2} + DH^{2}}$ = $\sqrt{(2\sqrt{3})^{2} + 1^{2}}$ = $\sqrt{13}$,AG = $\sqrt{AD^{2} - DG^{2}}$ = $\sqrt{(\sqrt{13})^{2} - 2^{2}}$ = 3,
∴AF = GF - AG = 4 - 3 = 1,AE = $\sqrt{AF^{2} + EF^{2}}$ = $\sqrt{1^{2} + 2^{2}}$ = $\sqrt{5}$,
∴当AG + AF最小时,AE = $\sqrt{5}$. 故选B.
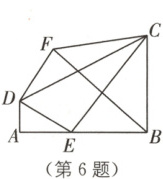
6. (安徽中考)如图,在四边形$ ABCD $中,$ \angle A = \angle ABC = 90° $,$ AB = 4 $,$ BC = 3 $,$ AD = 1 $,点$ E $为边$ AB $上的动点。将线段$ DE $绕点$ D $逆时针旋转$ 90° $得到线段$ DF $,连接$ FB $,$ FC $,$ EC $,则下列结论错误的是(
A.$ EC - ED $的最大值是$ 2\sqrt{5} $
B.$ FB $的最小值是$ \sqrt{10} $
C.$ EC + ED $的最小值是$ 4\sqrt{2} $
D.$ FC $的最大值是$ \sqrt{13} $
A
)。
A.$ EC - ED $的最大值是$ 2\sqrt{5} $
B.$ FB $的最小值是$ \sqrt{10} $
C.$ EC + ED $的最小值是$ 4\sqrt{2} $
D.$ FC $的最大值是$ \sqrt{13} $
答案:
6. A [解析]
∵将线段DE绕点D逆时针旋转90°得到线段DF,
∴DE = DF,∠EDF = 90°. 又∠A = ∠ABC = 90°,AB = 4,BC = 3,AD = 1. 如图
(1),过点D作DG⊥BC于点G,在DG上取一点H,使得DH = AD = 1,延长FH交AB于点I,则四边形ABGD是矩形,
∴∠GDA = ∠ADE + ∠EDG = 90° = ∠EDG + ∠HDF,
∴∠ADE = ∠HDF,
∴△DHF≌△DAE(SAS),
∴∠DHF = ∠DAE = 90°,
∴FH⊥DG,即点F在FH上运动,
∴四边形DAIH和四边形BGHI是矩形,
∴HI = AD = BG = 1,AI = DH = 1,BI = 4 - 1 = 3.
∵∠A = ∠ABC = 90°,AB = 4,BC = 3,AD = 1,
∴DE = $\sqrt{1^{2} + (4 - BE)^{2}}$,CE = $\sqrt{3^{2} + BE^{2}}$,
∴EC - ED = $\sqrt{3^{2} + BE^{2}} - \sqrt{1^{2} + (4 - BE)^{2}}$,
∴BE最大时,EC - ED最大.
如图
(2),当点E与点A重合,点F与点H重合时,

BF最小,此时EC = $\sqrt{4^{2} + 3^{2}}$ = 5,ED = 1,EC - ED = 5 - 1 = 4 ≠ $2\sqrt{5}$,故A错误,符合题意;BF = $\sqrt{HI^{2} + BI^{2}}$ = $\sqrt{1^{2} + 3^{2}}$ = $\sqrt{10}$,故B正确,不符合题意;
如图
(3),作点D关于AB的对称点M,连接MC,

则ED = EM,AD = AM = 1,∠BAM = ∠BAD = 90°,过点M作MN⊥CB于点N,此时EC + ED ≥ CM,当C,E,M三点共线时,EC + ED最小.
∵MN⊥CB,∠ABN = 180° - 90° = 90°,四边形AMNB是矩形,
∴BN = AM = 1,CN = 3 + 1 = 4,AB = MN = 4,
∴EC + ED的最小值 = MC = $\sqrt{4^{2} + 4^{2}}$ = $4\sqrt{2}$,故C正确,不符合题意;
当点E与点A重合时,CF = $\sqrt{GH^{2} + CG^{2}}$ = $\sqrt{(3 - 1)^{2} + (4 - 1)^{2}}$ = $\sqrt{13}$,当点E与点B重合时,过点C作CQ⊥FH,则四边形CQIB是矩形,如图
(4),
∴CQ = IB = 4 - 1 = 3,QI = BC = 3.
∵△DHF≌△DAE,
∴FH = AE = 4,
∴QF = FH + HI - QI = 4 + 1 - 3 = 2,
∴FC = $\sqrt{CQ^{2} + FQ^{2}}$ = $\sqrt{2^{2} + 3^{2}}$ = $\sqrt{13}$. 综上,FC最大值为$\sqrt{13}$. 故D正确,不符合题意. 故选A.
6. A [解析]
∵将线段DE绕点D逆时针旋转90°得到线段DF,
∴DE = DF,∠EDF = 90°. 又∠A = ∠ABC = 90°,AB = 4,BC = 3,AD = 1. 如图
(1),过点D作DG⊥BC于点G,在DG上取一点H,使得DH = AD = 1,延长FH交AB于点I,则四边形ABGD是矩形,
∴∠GDA = ∠ADE + ∠EDG = 90° = ∠EDG + ∠HDF,
∴∠ADE = ∠HDF,
∴△DHF≌△DAE(SAS),
∴∠DHF = ∠DAE = 90°,
∴FH⊥DG,即点F在FH上运动,
∴四边形DAIH和四边形BGHI是矩形,
∴HI = AD = BG = 1,AI = DH = 1,BI = 4 - 1 = 3.
∵∠A = ∠ABC = 90°,AB = 4,BC = 3,AD = 1,
∴DE = $\sqrt{1^{2} + (4 - BE)^{2}}$,CE = $\sqrt{3^{2} + BE^{2}}$,
∴EC - ED = $\sqrt{3^{2} + BE^{2}} - \sqrt{1^{2} + (4 - BE)^{2}}$,
∴BE最大时,EC - ED最大.
如图
(2),当点E与点A重合,点F与点H重合时,

BF最小,此时EC = $\sqrt{4^{2} + 3^{2}}$ = 5,ED = 1,EC - ED = 5 - 1 = 4 ≠ $2\sqrt{5}$,故A错误,符合题意;BF = $\sqrt{HI^{2} + BI^{2}}$ = $\sqrt{1^{2} + 3^{2}}$ = $\sqrt{10}$,故B正确,不符合题意;
如图
(3),作点D关于AB的对称点M,连接MC,

则ED = EM,AD = AM = 1,∠BAM = ∠BAD = 90°,过点M作MN⊥CB于点N,此时EC + ED ≥ CM,当C,E,M三点共线时,EC + ED最小.
∵MN⊥CB,∠ABN = 180° - 90° = 90°,四边形AMNB是矩形,
∴BN = AM = 1,CN = 3 + 1 = 4,AB = MN = 4,
∴EC + ED的最小值 = MC = $\sqrt{4^{2} + 4^{2}}$ = $4\sqrt{2}$,故C正确,不符合题意;
当点E与点A重合时,CF = $\sqrt{GH^{2} + CG^{2}}$ = $\sqrt{(3 - 1)^{2} + (4 - 1)^{2}}$ = $\sqrt{13}$,当点E与点B重合时,过点C作CQ⊥FH,则四边形CQIB是矩形,如图
(4),
∴CQ = IB = 4 - 1 = 3,QI = BC = 3.
∵△DHF≌△DAE,
∴FH = AE = 4,
∴QF = FH + HI - QI = 4 + 1 - 3 = 2,
∴FC = $\sqrt{CQ^{2} + FQ^{2}}$ = $\sqrt{2^{2} + 3^{2}}$ = $\sqrt{13}$. 综上,FC最大值为$\sqrt{13}$. 故D正确,不符合题意. 故选A.
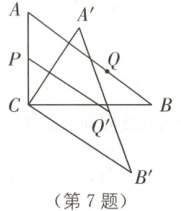
7. (泰州泰兴二模)如图,在$ \triangle ABC $中,$ \angle ACB = 90° $,$ AC = 6 $,$ BC = 8 $,$ P $为$ AC $的中点,点$ Q $为边$ AB $上一动点,将$ \triangle ABC $绕点$ C $顺时针旋转,点$ Q $的对应点记为$ Q' $,旋转过程中$ PQ' $的取值范围为
$1.8 \leqslant PQ' \leqslant 11$
。
答案:
7. $1.8 \leqslant PQ' \leqslant 11$ [解析]如图,过点C作CH⊥AB于点H.

∵∠ACB = 90°,
∴AB = $\sqrt{AC^{2} + BC^{2}}$ = 10,
∴$S_{\triangle ABC}$ = $\frac{1}{2}$AC·BC = $\frac{1}{2}$AB·CH = $\frac{1}{2}×6×8$ = 24,
∴CH = 4.8.
以点C为圆心,CH为半径画圆.
∵P为AC的中点,
∴CP = $\frac{1}{2}$AC = 3,由于点Q'在以点C为圆心,CH为半径的圆上能取到最小值,
∴PQ'的最小值为4.8 - 3 = 1.8.
由于AB上的点B距离C点最长,
∴点Q'在以点C为圆心,BC为半径的圆上能取到最大值,
∴PQ'的最大值为8 + 3 = 11,
∴旋转过程中PQ'的取值范围为$1.8 \leqslant PQ' \leqslant 11$.
7. $1.8 \leqslant PQ' \leqslant 11$ [解析]如图,过点C作CH⊥AB于点H.

∵∠ACB = 90°,
∴AB = $\sqrt{AC^{2} + BC^{2}}$ = 10,
∴$S_{\triangle ABC}$ = $\frac{1}{2}$AC·BC = $\frac{1}{2}$AB·CH = $\frac{1}{2}×6×8$ = 24,
∴CH = 4.8.
以点C为圆心,CH为半径画圆.
∵P为AC的中点,
∴CP = $\frac{1}{2}$AC = 3,由于点Q'在以点C为圆心,CH为半径的圆上能取到最小值,
∴PQ'的最小值为4.8 - 3 = 1.8.
由于AB上的点B距离C点最长,
∴点Q'在以点C为圆心,BC为半径的圆上能取到最大值,
∴PQ'的最大值为8 + 3 = 11,
∴旋转过程中PQ'的取值范围为$1.8 \leqslant PQ' \leqslant 11$.
8. 如图,已知$ Rt\triangle ABC $的两条直角边$ AC = 4 $,$ BC = 3 $,将$ Rt\triangle ABC $绕着直角边$ AC $中点$ G $旋转,得到$ \triangle DEF $,若$ \triangle DEF $的锐角顶点$ D $恰好落在$ \triangle ABC $的斜边$ AB $上,斜边$ DE $与$ AC $交于点$ H $,则$ CH = $

$\frac{28}{39}$
。
答案:
8. $\frac{28}{39}$ [解析]如图,连接CD.
∵AC = 4,BC = 3.

由勾股定理,得AB = 5.
∵G为AC的中点,
∴AG = DG.
∵△ADG是等腰三角形,
∴∠A = ∠ADG,
∴∠ADC = $\frac{1}{2}×180°$ = 90°.
∵cosA = $\frac{AD}{AC}$ = $\frac{AC}{AB}$,
∴$\frac{AD}{4}$ = $\frac{4}{5}$,
∴AD = $\frac{16}{5}$.
∵∠AHD = ∠DHG,∠HDG = ∠HAD,
∴△HDG∽△HAD,
∴$\frac{DG}{AD}$ = $\frac{HG}{DH}$,$\frac{DH}{HA}$ = $\frac{5}{8}$,设GH = 5x,则
DH = 8x,AH = 5x + 2,
∴$\frac{8x}{5x + 2}$ = $\frac{5}{8}$,解得x = $\frac{10}{39}$,经检验,x = $\frac{10}{39}$是方程的解,
∴AH = 5x + 2 = $\frac{128}{39}$,
∴CH = AC - AH = 4 - $\frac{128}{39}$ = $\frac{28}{39}$.
8. $\frac{28}{39}$ [解析]如图,连接CD.
∵AC = 4,BC = 3.

由勾股定理,得AB = 5.
∵G为AC的中点,
∴AG = DG.
∵△ADG是等腰三角形,
∴∠A = ∠ADG,
∴∠ADC = $\frac{1}{2}×180°$ = 90°.
∵cosA = $\frac{AD}{AC}$ = $\frac{AC}{AB}$,
∴$\frac{AD}{4}$ = $\frac{4}{5}$,
∴AD = $\frac{16}{5}$.
∵∠AHD = ∠DHG,∠HDG = ∠HAD,
∴△HDG∽△HAD,
∴$\frac{DG}{AD}$ = $\frac{HG}{DH}$,$\frac{DH}{HA}$ = $\frac{5}{8}$,设GH = 5x,则
DH = 8x,AH = 5x + 2,
∴$\frac{8x}{5x + 2}$ = $\frac{5}{8}$,解得x = $\frac{10}{39}$,经检验,x = $\frac{10}{39}$是方程的解,
∴AH = 5x + 2 = $\frac{128}{39}$,
∴CH = AC - AH = 4 - $\frac{128}{39}$ = $\frac{28}{39}$.
查看更多完整答案,请扫码查看


