《2025年实验班中考数学压轴题》

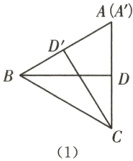
[典例] (珠海一模)[问题情境]在综合实践活动课上，李老师让同桌两位同学用相同的两块含$30°$角的三角板开展数学探究活动，两块三角板分别记作$\triangle ADB$和$\triangle A'D'C$，$\angle ADB = \angle A'D'C = 90°$，$\angle B = \angle C = 30°$，$AB = 2$。
[操作探究]如图(1)，先将$\triangle ADB$和$\triangle A'D'C$的边$AD$，$A'D'$重合，再将$\triangle A'D'C$绕着点$A$按顺时针方向旋转，旋转角为$\alpha(0° ＜ \alpha ＜ 180°)$，旋转过程中$\triangle ADB$保持不动，连接$BC$(如图(2))。

(1)当$\alpha = 60°$时，求$BC$的长度；
(2)如图(3)，当$BC = 2\sqrt{2}$时，求$\alpha$的度数；
(3)取$BC$的中点$O$，点$P$是平面内某个定点，连接$OP$，在运动过程中$OP$的长是个定值，点$P$的位置是$\boldsymbol{$AB的中点$}$，这个定值为$\boldsymbol{$1$}$，运动开始后$\angle AOD = \boldsymbol{$30°$}$。
思路分步拆解
(1)利用$60°$证明等边三角形，可求解$BC$的长。
(2)(第一步：求$\angle BAH$)过点$A$作$AH \perp BC$于点$H$。由已知得$BH = CH = \boldsymbol{$√2$}$，由勾股定理求$AH$，可知$\angle BAH = \boldsymbol{$45°$}$；
(第二步：求$\alpha$)求出$\angle BAC = \boldsymbol{$90°$}$，即可求解。
(3)(第一步：从变化的过程中确定不变的量)根据等腰三角形的性质可得$\angle AOB = \boldsymbol{$90°$}°$，从而得到点$O$的运动轨迹；
(第二步：求$OP$和$\angle AOD$)由$OP$为定值，可判断$P$为$AB$的中点，可得$OP = \boldsymbol{$1$}$，再利用圆周角定理，可得$\angle AOD = \boldsymbol{$30°$}$。

答案：
思路分步拆解：
(2)√2 45° 90°
(3)90° 1 30°
解：
(1)如图
(1).
∵∠ADB=∠A′D′C=90°,∠ABD=∠A′CD′=30°,
∴∠BAD=∠D′A′C=60°,
∴当α=60°时,点A,D′,B共线,点A,D,C共线.
∵AB=AC,
∴△ABC是等边三角形,
∴BC=AB=2.

(2)如图
(2),过点A作AH⊥BC于点H.
∵AB=AC,BC=2√2,
∴BH=CH=1/2BC=√2,∠BAC=2∠BAH,
∴AH=√(AB² - BH²)=√2,
∴AH=BH,
∴∠BAH=45°,
∴∠BAC=2∠BAH=90°,
∴α=60°+60° - 90°=30°.

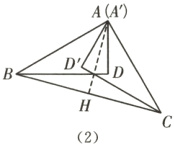
(3)AB的中点 1 30° [解析]
∵O是BC的中点,AB=AC,
∴AO⊥BC,即∠AOB=90°,
∴点O的运动轨迹为以AB为直径的圆,如图
(3)所示.
∵运动过程中OP的长是个定值,
∴P是AB的中点,这个定值为1/2AB=1.
∵∠ADB=90°,
∴点D在以AB为直径的圆上,
∴∠AOD=∠ABD=30°.