2025年实验班中考数学压轴题
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班中考数学压轴题 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第108页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
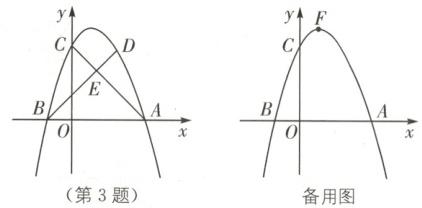
3. 参数法 (宜宾中考)如图,$O$是坐标原点,已知抛物线$y = -x^2 + bx + c$与$x$轴交于$A,B$两点,与$y$轴交于点$C$,其中$A(3,0),C(0,3)$。
(1) 求$b,c$的值;
(2) $D$为抛物线上第一象限内一点,连接$BD$,与直线$AC$交于点$E$,若$DE:BE = 1:2$,求点$D$的坐标;
(3) 若$F$为抛物线的顶点,平移抛物线使得新顶点为$P(m,n)(m > 1)$,若$P$又在原抛物线上,新抛物线与直线$x = 1$交于点$N$,连接$FP,PN,\angle FPN = 120°$。探究新抛物线与$x$轴是否存在两个不同的交点。若存在,求出这两个交点之间的距离;若不存在,请说明理由。
(1) 求$b,c$的值;
(2) $D$为抛物线上第一象限内一点,连接$BD$,与直线$AC$交于点$E$,若$DE:BE = 1:2$,求点$D$的坐标;
(3) 若$F$为抛物线的顶点,平移抛物线使得新顶点为$P(m,n)(m > 1)$,若$P$又在原抛物线上,新抛物线与直线$x = 1$交于点$N$,连接$FP,PN,\angle FPN = 120°$。探究新抛物线与$x$轴是否存在两个不同的交点。若存在,求出这两个交点之间的距离;若不存在,请说明理由。

答案:
3.
(1)依题意,分别把$A(3,0),C(0,3)$代入$y=-x^{2}+bx+c$,
得$\begin{cases}0=-9+3b+c,\\3=c.\end{cases}$解得$\begin{cases}b=2,\\c=3.\end{cases}$
(2)由
(1),得$b=2$,$c=3$,则$y=-x^{2}+2x+3$,$C(0,3)$,
令$y=0$,则$0=-x^{2}+2x+3=(-x+3)(x+1)$,
$\therefore x_{1}=3$,$x_{2}=-1$,$\therefore B(-1,0)$,$A(3,0)$.
分别过点$E$,$D$作$EN\perp OA$,$DM\perp OA$,如图
(1)所示.
$\because EN\perp OA$,$DM\perp OA$,
$\therefore\angle ENB=\angle DMB=90^{\circ}$.
$\because\angle DBM=\angle EBN$,
$\therefore\triangle DMB\sim\triangle ENB$,$\therefore\frac{DM}{EN}=\frac{BD}{BE}$.
$\because DE:BE=1:2$,
$\therefore DB:BE=3:2$,
$\therefore\frac{DM}{EN}=\frac{3}{2}$.
设点$E$的纵坐标为$2m$,则点$D$的纵坐标为$3m$,
设$AC$的解析式为$y=kx+r(k\neq0)$.
$\because C(0,3)$,$A(3,0)$,$\therefore\begin{cases}3=r,\\0=3k+r.\end{cases}$解得$\begin{cases}k=-1,\\r=3.\end{cases}$
$\therefore AC$的解析式为$y=-x+3$.
把$y=2m$代入$y=-x+3$,$\therefore x=3-2m$,$\therefore E(3-2m,2m)$.
设$BE$的解析式为$y=tx+q(t\neq0)$,
把$E(3-2m,2m)$,$B(-1,0)$代入$y=tx+q$,
得$\begin{cases}2m=t(3-2m)+q,\\0=-t+q.\end{cases}$解得$\begin{cases}t=\frac{m}{2-m},\\q=\frac{m}{2-m}.\end{cases}$
$\therefore BE$的解析式为$y=\frac{m}{2-m}x+\frac{m}{2-m}=\frac{m}{2-m}(x+1)$.
依题意,把$y=3m$代入$y=\frac{m}{2-m}(x+1)$,
得$3m=\frac{m}{2-m}(x+1)$,则$x=5-3m$,
即点$D(5-3m,3m)$.
$\because D$为抛物线上第一象限内一点,且$y=-x^{2}+2x+3$,
$\therefore3m=-(5-3m)^{2}+2(5-3m)+3$,
整理,得$3m^{2}-7m+4=(m-1)(3m-4)=0$,
$\therefore m_{1}=1$,$m_{2}=\frac{4}{3}$.
此时$y=\frac{m}{2-m}(x+1)$中$2-m\neq0$且$\frac{m}{2-m}\neq0$,
故$m_{1}=1$,$m_{2}=\frac{4}{3}$是符合题意的.
当$m=1$时,则$5-3m=5-3=2$,$3m=3$,此时$D(2,3)$,
当$m=\frac{4}{3}$时,则$5-3m=5-4=1$,$3m=3×\frac{4}{3}=4$,此时$D(1,4)$. 综上所述,$D(2,3)$或$D(1,4)$.
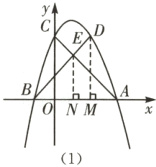
(3)存在,新抛物线与$x$轴的两个不同的交点之间的距离为2. 理由如下:由
(2),得$y=-x^{2}+2x+3$,
$\because F$为抛物线的顶点,$\therefore F(1,4)$.
$\because$平移抛物线使得新顶点为$P(m,n)(m>1)$,$P$又在原抛物线上,新抛物线与直线$x=1$交于点$N$,
连接$FP$,$PN$,过点$P$作$PH\perp FN$,$\angle FPN=120^{\circ}$,如图
(2)所示.
$\therefore$平移后的抛物线的解析式为$y=-(x-m)^{2}+n$,
把$x=1$代入$y=-(x-m)^{2}+n$,
得$y_{N}=-(1-m)^{2}+n$.
$\because$点$P(m,n)$在$y=-(x-1)^{2}+4$上,
$\therefore n=-(m-1)^{2}+4$,
$\therefore y_{N}=-(1-m)^{2}+n=-4+n+n=-4+2n$.
$\because P(m,n)$,$N(1,-4+2n)$,$F(1,4)$,
$\therefore PF^{2}=(m-1)^{2}+(n-4)^{2}$,$PN^{2}=(m-1)^{2}+[n-(-4+2n)]^{2}=(m-1)^{2}+(4-n)^{2}$,则$PF^{2}=PN^{2}$,
即$PF=PN$,$\therefore\triangle PFN$是等腰三角形.
$\because\angle FPN=120^{\circ}$,$\therefore\angle FPH=\frac{1}{2}×120^{\circ}=60^{\circ}$,
则$\tan\angle FPH=\tan60^{\circ}=\frac{FH}{HP}=\sqrt{3}$,
$\therefore4-n=\sqrt{3}(m-1)$.
令$t=m-1$,$\therefore4-n=\sqrt{3}t$,即$n=-\sqrt{3}t+4$.
$\because n=-(m-1)^{2}+4$,$\therefore-\sqrt{3}t+4=-t^{2}+4$,
即$t^{2}-\sqrt{3}t=0$,
$\therefore t_{1}=0$,$t_{2}=\sqrt{3}$,$\therefore m-1=0$或$m-1=\sqrt{3}$,
$\therefore m=1$(舍去)或$m=\sqrt{3}+1$,$\therefore P(1+\sqrt{3},1)$,
$\therefore$平移后的抛物线解析式为$y=-(x-1-\sqrt{3})^{2}+1$.
令$y=0$,则$0=-(x-1-\sqrt{3})^{2}+1$,
$\therefore(x-1-\sqrt{3})^{2}=1$,$\therefore x_{1}=2+\sqrt{3}$,$x_{2}=\sqrt{3}$,
则$\vert x_{1}-x_{2}\vert=2+\sqrt{3}-\sqrt{3}=2$,
$\therefore$新抛物线与$x$轴存在两个不同的交点,这两个交点之间的距离为2.

3.
(1)依题意,分别把$A(3,0),C(0,3)$代入$y=-x^{2}+bx+c$,
得$\begin{cases}0=-9+3b+c,\\3=c.\end{cases}$解得$\begin{cases}b=2,\\c=3.\end{cases}$
(2)由
(1),得$b=2$,$c=3$,则$y=-x^{2}+2x+3$,$C(0,3)$,
令$y=0$,则$0=-x^{2}+2x+3=(-x+3)(x+1)$,
$\therefore x_{1}=3$,$x_{2}=-1$,$\therefore B(-1,0)$,$A(3,0)$.
分别过点$E$,$D$作$EN\perp OA$,$DM\perp OA$,如图
(1)所示.
$\because EN\perp OA$,$DM\perp OA$,
$\therefore\angle ENB=\angle DMB=90^{\circ}$.
$\because\angle DBM=\angle EBN$,
$\therefore\triangle DMB\sim\triangle ENB$,$\therefore\frac{DM}{EN}=\frac{BD}{BE}$.
$\because DE:BE=1:2$,
$\therefore DB:BE=3:2$,
$\therefore\frac{DM}{EN}=\frac{3}{2}$.
设点$E$的纵坐标为$2m$,则点$D$的纵坐标为$3m$,
设$AC$的解析式为$y=kx+r(k\neq0)$.
$\because C(0,3)$,$A(3,0)$,$\therefore\begin{cases}3=r,\\0=3k+r.\end{cases}$解得$\begin{cases}k=-1,\\r=3.\end{cases}$
$\therefore AC$的解析式为$y=-x+3$.
把$y=2m$代入$y=-x+3$,$\therefore x=3-2m$,$\therefore E(3-2m,2m)$.
设$BE$的解析式为$y=tx+q(t\neq0)$,
把$E(3-2m,2m)$,$B(-1,0)$代入$y=tx+q$,
得$\begin{cases}2m=t(3-2m)+q,\\0=-t+q.\end{cases}$解得$\begin{cases}t=\frac{m}{2-m},\\q=\frac{m}{2-m}.\end{cases}$
$\therefore BE$的解析式为$y=\frac{m}{2-m}x+\frac{m}{2-m}=\frac{m}{2-m}(x+1)$.
依题意,把$y=3m$代入$y=\frac{m}{2-m}(x+1)$,
得$3m=\frac{m}{2-m}(x+1)$,则$x=5-3m$,
即点$D(5-3m,3m)$.
$\because D$为抛物线上第一象限内一点,且$y=-x^{2}+2x+3$,
$\therefore3m=-(5-3m)^{2}+2(5-3m)+3$,
整理,得$3m^{2}-7m+4=(m-1)(3m-4)=0$,
$\therefore m_{1}=1$,$m_{2}=\frac{4}{3}$.
此时$y=\frac{m}{2-m}(x+1)$中$2-m\neq0$且$\frac{m}{2-m}\neq0$,
故$m_{1}=1$,$m_{2}=\frac{4}{3}$是符合题意的.
当$m=1$时,则$5-3m=5-3=2$,$3m=3$,此时$D(2,3)$,
当$m=\frac{4}{3}$时,则$5-3m=5-4=1$,$3m=3×\frac{4}{3}=4$,此时$D(1,4)$. 综上所述,$D(2,3)$或$D(1,4)$.

(3)存在,新抛物线与$x$轴的两个不同的交点之间的距离为2. 理由如下:由
(2),得$y=-x^{2}+2x+3$,
$\because F$为抛物线的顶点,$\therefore F(1,4)$.
$\because$平移抛物线使得新顶点为$P(m,n)(m>1)$,$P$又在原抛物线上,新抛物线与直线$x=1$交于点$N$,
连接$FP$,$PN$,过点$P$作$PH\perp FN$,$\angle FPN=120^{\circ}$,如图
(2)所示.
$\therefore$平移后的抛物线的解析式为$y=-(x-m)^{2}+n$,
把$x=1$代入$y=-(x-m)^{2}+n$,
得$y_{N}=-(1-m)^{2}+n$.
$\because$点$P(m,n)$在$y=-(x-1)^{2}+4$上,
$\therefore n=-(m-1)^{2}+4$,
$\therefore y_{N}=-(1-m)^{2}+n=-4+n+n=-4+2n$.
$\because P(m,n)$,$N(1,-4+2n)$,$F(1,4)$,
$\therefore PF^{2}=(m-1)^{2}+(n-4)^{2}$,$PN^{2}=(m-1)^{2}+[n-(-4+2n)]^{2}=(m-1)^{2}+(4-n)^{2}$,则$PF^{2}=PN^{2}$,
即$PF=PN$,$\therefore\triangle PFN$是等腰三角形.
$\because\angle FPN=120^{\circ}$,$\therefore\angle FPH=\frac{1}{2}×120^{\circ}=60^{\circ}$,
则$\tan\angle FPH=\tan60^{\circ}=\frac{FH}{HP}=\sqrt{3}$,
$\therefore4-n=\sqrt{3}(m-1)$.
令$t=m-1$,$\therefore4-n=\sqrt{3}t$,即$n=-\sqrt{3}t+4$.
$\because n=-(m-1)^{2}+4$,$\therefore-\sqrt{3}t+4=-t^{2}+4$,
即$t^{2}-\sqrt{3}t=0$,
$\therefore t_{1}=0$,$t_{2}=\sqrt{3}$,$\therefore m-1=0$或$m-1=\sqrt{3}$,
$\therefore m=1$(舍去)或$m=\sqrt{3}+1$,$\therefore P(1+\sqrt{3},1)$,
$\therefore$平移后的抛物线解析式为$y=-(x-1-\sqrt{3})^{2}+1$.
令$y=0$,则$0=-(x-1-\sqrt{3})^{2}+1$,
$\therefore(x-1-\sqrt{3})^{2}=1$,$\therefore x_{1}=2+\sqrt{3}$,$x_{2}=\sqrt{3}$,
则$\vert x_{1}-x_{2}\vert=2+\sqrt{3}-\sqrt{3}=2$,
$\therefore$新抛物线与$x$轴存在两个不同的交点,这两个交点之间的距离为2.

4. 中考新考法 双动点问题 (齐齐哈尔中考)综合与探究
如图(1),在平面直角坐标系中,抛物线$y = ax^2 + bx + 3(a < 0)$与$x$轴交于点$A(-1,0)$、$C(6,0)$,与$y$轴交于点$B$,连接$BC$。
(1) 求抛物线的解析式;
(2) $P$是直线$BC$下方抛物线上的点,连接$PB,PC$,当$S_{\triangle PBC} = 24$时,求点$P$的坐标;
(3) $G$是第四象限内抛物线上的一点,连接$BG$,若$\angle CBG = 45°$,则点$G$的坐标为$\boldsymbol{$
(4) 如图(2),作点$B$关于$x$轴的对称点$D$,过点$D$作$x$轴的平行线$l$,过点$C$作$CE \perp l$,垂足为$E$,动点$M,N$分别从点$O,E$同时出发,动点$M$以每秒$1$个单位长度的速度沿射线$OC$方向匀速运动,动点$N$以每秒$2$个单位长度的速度沿射线$ED$方向匀速运动(当点$N$到达点$D$时,点$M,N$都停止运动),连接$MN$,过点$D$作$MN$的垂线,垂足为$F$,连接$CF$,则$CF$的取值范围是$\boldsymbol{$
答案见$\boldsymbol{P61}$

如图(1),在平面直角坐标系中,抛物线$y = ax^2 + bx + 3(a < 0)$与$x$轴交于点$A(-1,0)$、$C(6,0)$,与$y$轴交于点$B$,连接$BC$。
(1) 求抛物线的解析式;
(2) $P$是直线$BC$下方抛物线上的点,连接$PB,PC$,当$S_{\triangle PBC} = 24$时,求点$P$的坐标;
(3) $G$是第四象限内抛物线上的一点,连接$BG$,若$\angle CBG = 45°$,则点$G$的坐标为$\boldsymbol{$
$(11,-30)$
$}$;(4) 如图(2),作点$B$关于$x$轴的对称点$D$,过点$D$作$x$轴的平行线$l$,过点$C$作$CE \perp l$,垂足为$E$,动点$M,N$分别从点$O,E$同时出发,动点$M$以每秒$1$个单位长度的速度沿射线$OC$方向匀速运动,动点$N$以每秒$2$个单位长度的速度沿射线$ED$方向匀速运动(当点$N$到达点$D$时,点$M,N$都停止运动),连接$MN$,过点$D$作$MN$的垂线,垂足为$F$,连接$CF$,则$CF$的取值范围是$\boldsymbol{$
$\sqrt{29}-\sqrt{2}\leqslant CF\leqslant3\sqrt{5}$
$}$。答案见$\boldsymbol{P61}$

答案:
4.
(1)将$A(-1,0),C(6,0)$代入抛物线的解析式$y=ax^{2}+bx+3$,得$\begin{cases}a-b+3=0,\\36a+6b+3=0.\end{cases}$解得$\begin{cases}a=-\frac{1}{2},\\b=\frac{5}{2}.\end{cases}$
$\therefore$抛物线的解析式为$y=-\frac{1}{2}x^{2}+\frac{5}{2}x+3$.
(2)过点$P$作$PQ// BC$交$y$轴于点$Q$,如图
(1)所示,
则$S_{\triangle QBC}=S_{\triangle PBC}=24$,
$\therefore\frac{1}{2}BQ· CO=24$,
$\because$点$C(6,0)$,则$CO=6$,$\therefore BQ=8$.
又$B(0,3)$,$\therefore$点$Q(0,-5)$.
$\therefore$直线$BC$的解析式为$y=-\frac{1}{2}x+3$.
$\because PQ// BC$,$\therefore$直线$PQ$的解析式为$y=-\frac{1}{2}x-5$,
联立,得$\begin{cases}y=-\frac{1}{2}x-5,\\y=-\frac{1}{2}x^{2}+\frac{5}{2}x+3.\end{cases}$
解得$\begin{cases}x=-2,\\y=-4\end{cases}$或$\begin{cases}x=8,\\y=-9.\end{cases}$
故点$P$的坐标为$(-2,-4)$或$(8,-9)$.

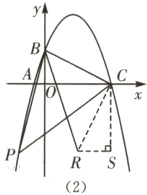
(3)$(11,-30)$ [解析] 将$Rt\triangle CBO$绕点$C$逆时针旋转$90^{\circ}$得到$Rt\triangle CRS$,则$\triangle BCR$为等腰直角三角形.
从而$\angle CBR=45^{\circ}$,如图
(2)所示.
又$G$是第四象限内抛物线上的一点,$\angle CBG=45^{\circ}$,
$\therefore G$为$BR$延长线与抛物线的交点.
由旋转可知,$\angle BOC=\angle RSC=90^{\circ}$,$BO=RS=3$,$OC=SC=6$. 故点$R$的坐标为$(3,-6)$.
由待定系数法可知,直线$BR$的解析式为$y=-3x+3$,
联立$y=-3x+3$与$y=-\frac{1}{2}x^{2}+\frac{5}{2}x+3$,整理可得$x^{2}-11x=0$,解得$x=11$或$0$(舍去).
故点$G$的坐标为$(11,-30)$.
(4)$\sqrt{29}-\sqrt{2}\leqslant CF\leqslant3\sqrt{5}$ [解析] 由题意知,四边形$OCED$为矩形,$OD=BO=3$,$DE=OC=6$.
连接$OE$,交$MN$于点$G$,如图
(3)所示,
故$OE=\sqrt{DE^{2}+OD^{2}}=\sqrt{36+9}=3\sqrt{5}$.
$\because OM// EN$,
$\therefore\triangle OMG\sim\triangle ENG$,
$\therefore\frac{OG}{EG}=\frac{OM}{EN}=\frac{1}{2}$,$\frac{EG}{OE}=\frac{2}{3}$.
过点$G$作$GH\perp DE$于点$H$,
$\because GH// OD$,
$\therefore\triangle GHE\sim\triangle ODE$,
$\therefore\frac{EG}{EO}=\frac{GH}{OD}=\frac{HE}{DE}=\frac{2}{3}$,
$\therefore GH=\frac{2}{3}OD=2$,$HE=\frac{2}{3}DE=4$,$DH=6-4=2$,
故$\sqrt{GH^{2}+DH^{2}}=\sqrt{2^{2}+2^{2}}=DG=2\sqrt{2}$.
取$DG$中点$J$,连接$FJ$,$CJ$,
$\because\angle DFG=90^{\circ}$,
$\therefore$根据斜边中线定理可得$FJ=\frac{1}{2}DG=\sqrt{2}$,
故$CF\geqslant CJ-FJ$,当且仅当$J$,$F$,$C$三点共线时取等号.
易知点$J$坐标为$(1,-2)$,$C(6,0)$,
故$CJ=\sqrt{5^{2}+2^{2}}=\sqrt{29}$,则$CF\geqslant CJ-FJ=\sqrt{29}-\sqrt{2}$.
当点$N$与点$D$重合时,点$F$与点$D$重合,此时$CF$最大,即$CF=OE=3\sqrt{5}$,
综上所述,$CF$的取值范围为$\sqrt{29}-\sqrt{2}\leqslant CF\leqslant3\sqrt{5}$.

4.
(1)将$A(-1,0),C(6,0)$代入抛物线的解析式$y=ax^{2}+bx+3$,得$\begin{cases}a-b+3=0,\\36a+6b+3=0.\end{cases}$解得$\begin{cases}a=-\frac{1}{2},\\b=\frac{5}{2}.\end{cases}$
$\therefore$抛物线的解析式为$y=-\frac{1}{2}x^{2}+\frac{5}{2}x+3$.
(2)过点$P$作$PQ// BC$交$y$轴于点$Q$,如图
(1)所示,
则$S_{\triangle QBC}=S_{\triangle PBC}=24$,
$\therefore\frac{1}{2}BQ· CO=24$,
$\because$点$C(6,0)$,则$CO=6$,$\therefore BQ=8$.
又$B(0,3)$,$\therefore$点$Q(0,-5)$.
$\therefore$直线$BC$的解析式为$y=-\frac{1}{2}x+3$.
$\because PQ// BC$,$\therefore$直线$PQ$的解析式为$y=-\frac{1}{2}x-5$,
联立,得$\begin{cases}y=-\frac{1}{2}x-5,\\y=-\frac{1}{2}x^{2}+\frac{5}{2}x+3.\end{cases}$
解得$\begin{cases}x=-2,\\y=-4\end{cases}$或$\begin{cases}x=8,\\y=-9.\end{cases}$
故点$P$的坐标为$(-2,-4)$或$(8,-9)$.


(3)$(11,-30)$ [解析] 将$Rt\triangle CBO$绕点$C$逆时针旋转$90^{\circ}$得到$Rt\triangle CRS$,则$\triangle BCR$为等腰直角三角形.
从而$\angle CBR=45^{\circ}$,如图
(2)所示.
又$G$是第四象限内抛物线上的一点,$\angle CBG=45^{\circ}$,
$\therefore G$为$BR$延长线与抛物线的交点.
由旋转可知,$\angle BOC=\angle RSC=90^{\circ}$,$BO=RS=3$,$OC=SC=6$. 故点$R$的坐标为$(3,-6)$.
由待定系数法可知,直线$BR$的解析式为$y=-3x+3$,
联立$y=-3x+3$与$y=-\frac{1}{2}x^{2}+\frac{5}{2}x+3$,整理可得$x^{2}-11x=0$,解得$x=11$或$0$(舍去).
故点$G$的坐标为$(11,-30)$.
(4)$\sqrt{29}-\sqrt{2}\leqslant CF\leqslant3\sqrt{5}$ [解析] 由题意知,四边形$OCED$为矩形,$OD=BO=3$,$DE=OC=6$.
连接$OE$,交$MN$于点$G$,如图
(3)所示,
故$OE=\sqrt{DE^{2}+OD^{2}}=\sqrt{36+9}=3\sqrt{5}$.
$\because OM// EN$,
$\therefore\triangle OMG\sim\triangle ENG$,
$\therefore\frac{OG}{EG}=\frac{OM}{EN}=\frac{1}{2}$,$\frac{EG}{OE}=\frac{2}{3}$.
过点$G$作$GH\perp DE$于点$H$,
$\because GH// OD$,
$\therefore\triangle GHE\sim\triangle ODE$,
$\therefore\frac{EG}{EO}=\frac{GH}{OD}=\frac{HE}{DE}=\frac{2}{3}$,
$\therefore GH=\frac{2}{3}OD=2$,$HE=\frac{2}{3}DE=4$,$DH=6-4=2$,
故$\sqrt{GH^{2}+DH^{2}}=\sqrt{2^{2}+2^{2}}=DG=2\sqrt{2}$.
取$DG$中点$J$,连接$FJ$,$CJ$,
$\because\angle DFG=90^{\circ}$,
$\therefore$根据斜边中线定理可得$FJ=\frac{1}{2}DG=\sqrt{2}$,
故$CF\geqslant CJ-FJ$,当且仅当$J$,$F$,$C$三点共线时取等号.
易知点$J$坐标为$(1,-2)$,$C(6,0)$,
故$CJ=\sqrt{5^{2}+2^{2}}=\sqrt{29}$,则$CF\geqslant CJ-FJ=\sqrt{29}-\sqrt{2}$.
当点$N$与点$D$重合时,点$F$与点$D$重合,此时$CF$最大,即$CF=OE=3\sqrt{5}$,
综上所述,$CF$的取值范围为$\sqrt{29}-\sqrt{2}\leqslant CF\leqslant3\sqrt{5}$.

查看更多完整答案,请扫码查看


