《2025年实验班中考数学压轴题》

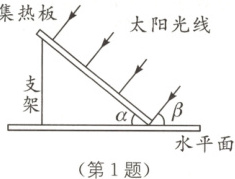
1. 新情境 了解集热板 (兰州中考)如图是集热板示意图，集热板与太阳光线垂直时，光能利用率最高。春分日兰州正午太阳光线与水平面的夹角$\beta$为$54^{\circ}$。若光能利用率最高，则集热板与水平面夹角$\alpha$度数是(C)。

A.$26^{\circ}$
B.$30^{\circ}$
C.$36^{\circ}$
D.$54^{\circ}$

答案： 1.C　[解析]
∵集热板与太阳光线垂直，
∴α+β=180°−90°=90°.
∵β=54°,
∴α=90°−β=36°.故选C.

2. (肇庆四会华赋实验学校三模)机器狗是一种模拟真实犬只形态和部分行为的机器装置，最快移动速度$v(\mathrm{m/s})$是载重后总质量$M(\mathrm{kg})$的反比例函数。已知一款机器狗载重后总质量$M = 30\ \mathrm{kg}$时，它的最快移动速度$v = 2\ \mathrm{m/s}$；当其载重后总质量$M = 60\ \mathrm{kg}$时，它的最快移动速度$v$为(D)。

A.$4\ \mathrm{m/s}$
B.$3\ \mathrm{m/s}$
C.$2\ \mathrm{m/s}$
D.$1\ \mathrm{m/s}$

答案： 2.D　[解析]设v与M的函数关系式为v=$\frac{k}{M}$(k为常数，且k≠0).将M=30,v=2代入v=$\frac{k}{M}$，得2=$\frac{k}{30}$，解得k=60,
∴v与M的函数关系式为v=$\frac{60}{M}$.当M=60时，v=$\frac{60}{60}$=1,
∴当其载重后总质量M=60kg时，它的最快移动速度v=1m/s.故选D.

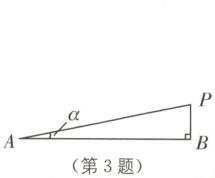
3. (浙江中考)无人机警戒在高速公路场景中的应用，是我国低空经济高质量发展的重要实践方向。如图，在高速公路上，交警在$A$处操控无人机巡查，无人机从点$A$处飞行到点$P$处悬停，探测到它的正下方公路上点$B$处有汽车发生故障。测得$A$处到$P$处的距离为$500\ \mathrm{m}$，从点$A$观测点$P$的仰角为$\alpha$，$\cos\alpha = 0.98$，则$A$处到$B$处的距离为$\boldsymbol{$490$}\ \mathrm{m}$。

答案： 3.490　[解析]在Rt△ABP中,∠B=90°,AP=500m,∠A=α,
∴AB=AP·cosα=500×0.98=490(m).故A处到点B处的距离为490m.

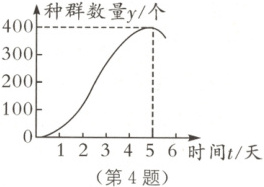
4. 新情境 培养大草履虫实验 (广西中考)生态学家$G.F.\mathrm{Gause}$通过多次单独培养大草履虫实验，研究其种群数量$y$随时间$t$的变化情况，得到了如图所示的“$S$”形曲线。下列说法正确的是(B)。

A.第$5$天的种群数量为$300$个
B.前$3$天种群数量持续增长
C.第$3$天的种群数量达到最大
D.每天增加的种群数量相同

答案： 4.B[解析]A.第5天的种群数量为400个，原说法错误，该选项不符合题意;B.前3天种群数量持续增长，说法正确，该选项符合题意;C.第5天的种群数量达到最大，原说法错误，该选项不符合题意;D.每天增加的种群数量不相同，原说法错误，该选项不符合题意.故选B

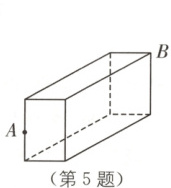
5. 如图是一个长为$12\ \mathrm{cm}$，宽为$5\ \mathrm{cm}$，高为$8\ \mathrm{cm}$的长方体，一只蜘蛛从一条侧棱的中点$A$沿着长方体表面爬行到顶点$B$去捕捉蚂蚁，此时蜘蛛爬行的最短距离是(B)。

A.$13\ \mathrm{cm}$
B.$15\ \mathrm{cm}$
C.$21\ \mathrm{cm}$
D.$25\ \mathrm{cm}$

答案：
5.B　[解析]如图,路线①:AB=$\sqrt{5^{2}+(12+8÷2)^{2}}$=$\sqrt{281}$(cm),路线②:AB=$\sqrt{4^{2}+(5+12)^{2}}$=$\sqrt{305}$(cm),路线③:AB=$\sqrt{(4+5)^{2}+12^{2}}$=15(cm).
∵$\sqrt{305}$＞$\sqrt{281}$＞15,
∴此时蜘蛛爬行的最短距离是15cm.故选B
　　　　　　

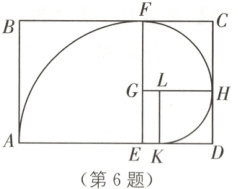
6. (兰州中考)如图，黄金矩形$ABCD$中$\dfrac{AB}{AD}=\dfrac{\sqrt{5}-1}{2}$，以宽$AB$为边在其内部作正方形$ABFE$，得到四边形$CDEF$是黄金矩形。依此作法，四边形$DEGH$，四边形$KEGL$也是黄金矩形。依次以点$E$，$G$，$L$为圆心作$\overset{\frown}{AF}$，$\overset{\frown}{FH}$，$\overset{\frown}{HK}$，曲线$AFHK$叫作“黄金螺线”。若$AD = 2$，则“黄金螺线”$AFHK$的长为$\boldsymbol{$($\sqrt{5}$−1)π$}$(结果用$\pi$表示)。

答案： 6.($\sqrt{5}$−1)π　[解析]
∵在黄金矩形ABCD中，$\frac{AB}{AD}$=$\frac{\sqrt{5}−1}{2}$,且AD=2,
∴AB=$\sqrt{5}$−1.
∵四边形ABFE是正方形，
∴AE=EF=BF=AB=$\sqrt{5}$−1,
∴FC=ED=2−($\sqrt{5}$−1)=3−$\sqrt{5}$.
∵四边形FGHC是正方形，
∴GF=GH=HC=FC=3−$\sqrt{5}$.
∵CD=AB=$\sqrt{5}$−1,
∴HD=CD−CH=($\sqrt{5}$−1)−(3−$\sqrt{5}$)=2$\sqrt{5}$−4.
∵四边形LKDH是正方形，
∴LH=HD=2$\sqrt{5}$−4,
∴“黄金螺线”AFHK的长为$\frac{90π·AE}{180}$+$\frac{90π·GH}{180}$+$\frac{90π·LH}{180}$=$\frac{1}{2}$π(AE+GH+LH)=$\frac{1}{2}$π(AD+LH)=$\frac{1}{2}$π(2+2$\sqrt{5}$−4)=($\sqrt{5}$−1)π.

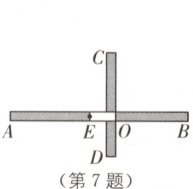
7. 新情境 围建劳动实践基地 (自贡中考)九(1)班劳动实践基地内有一块面积足够大的平整空地，地上两段围墙$AB\perp CD$于点$O$(如图)，其中$AB$上的$EO$段围墙空缺。同学们测得$AE = 6.6\ \mathrm{m}$，$OE = 1.4\ \mathrm{m}$，$OB = 6\ \mathrm{m}$，$OC = 5\ \mathrm{m}$，$OD = 3\ \mathrm{m}$，班长买来可切断的围栏$16\ \mathrm{m}$，准备利用已有围墙，围出一块封闭的矩形菜地，则该菜地最大面积是$\boldsymbol{$46.4$}\ \mathrm{m}^2$。
答案见$\mathrm{P}41$

答案：
7.46.4　[解析]设矩形在射线OA上的一段长为xm.①当x≤8时,如图
(1),S=x·$\frac{16−x−1.4+5}{2}$=−$\frac{1}{2}$x²+9.8x=−$\frac{1}{2}$(x−9.8)²+48.02,当x=8时,S取最大值，为46.4;②当x＞8时,如图
(2),S=x($\frac{16+6.6+5}{2}$−x)=−x²+13.8x=−(x−6.9)²+47.61,由于在x＞8的范围内,S均小于46.4,所以最大面积为46.4m².