《2025年实验班中考数学压轴题》

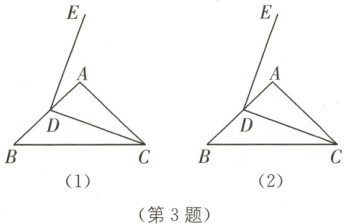
3. 如图(1),在$\triangle ABC$中,$\angle B = \angle ACB = \alpha$,点$D$是腰$AB$上一个动点(不与点$A$,$B$重合),连接$DC$,将线段$DC$绕点$D$逆时针旋转$2\alpha$得到线段$DE$.
(1)求证:$\angle ADE = \angle ACD$.
(2)如图(2),连接$BE$,取$BE$中点$F$,连接$AF$,$DF$.
①依题意补全图形;
②求$\angle AFD$的大小.

答案：
3.
(1)设∠ACD = β.
∵∠B = ∠ACB = α,
∴∠BCD = α - β,
∴∠ADC = ∠B + ∠BCD = 2α - β.
∵将线段DC绕点D逆时针旋转2α得到线段DE，
∴∠CDE = 2α,
∴∠ADE = ∠CDE - ∠ADC = β,
∴∠ADE = ∠ACD.
(2)①补全图形如图
(1)所示.
②如图
(2),延长BA到H,使DH = AB,连接EH,AE,延长AF到点G,使GF = AF,连接BG,DG,
∵AB = AC,
∴HD = AC.
由旋转的性质，可得DE = DC,
在△HDE和△ACD中,$\begin{cases} DE = CD, \\ \angle HDE = \angle ACD, \\ HD = AC, \end{cases}$
∴△HDE≌△ACD(SAS),
∴EH = AD.
∵F是BE中点，
∴BF = EF.
在△BGF和△EAF中,$\begin{cases} GF = AF, \\ \angle BFG = \angle EFA, \\ BF = EF, \end{cases}$
∴△BGF≌△EAF(SAS),
∴BG = AE,∠GBF = ∠AEF　　　　　　,
内错角相等，两直线平行AE//BG;
∴∠GBD = ∠EAH.
∵AB = DH,
∴BD = AH,
在△BGD和△AEH中,$\begin{cases} BG = AE, \\ \angle GBD = \angle EAH, \\ BD = AH, \end{cases}$
∴△BGD≌△AEH(SAS),
∴DG = EH,
∴DG = AD.
∵FG = AF,
∴DF⊥AG,
∴∠AFD = 90°.

4. 如图,在$\triangle ABC$中,$AB = 5$,$BC = 11$,$\triangle ABC$的面积为$22$,$AE \perp BC$于点$E$,动点$P$从点$A$出发,沿折线$AB - BC$向终点$C$运动,在$AB$上的速度为每秒$5$个单位长度,在$BC$上的速度为每秒$2$个单位长度,当点$P$出发后,且不与点$E$重合时,将点$E$绕$PA$的中点旋转$180°$得到点$F$,连接$AF$,$PF$,$PE$.设点$P$的运动时间为$t$(秒)$(t ＞ 0)$.
(1)$AE$的长为4;
(2)用含$t$的代数式表示四边形$AFPE$的面积$S$;
(3)当四边形$AFPE$被直线$AC$分得的两部分面积之比为$1:3$时,求$t$的值;
(4)当直线$CF$垂直于$\triangle ABC$的一边所在的直线时,直接写出$t$的值.
精题详解

答案：
4.
(1)4 [解析]
∵BC = 11,△ABC的面积为22,AE⊥BC,
∴$S△ABC = \frac{1}{2}BC·AE = 22,$
∴AE = (22×2)÷11 = 4.
(2)
∵AE⊥BC,AB = 5,AE = 4,
∴BE = 3,
∴CE = BC - BE = 11 - 3 = 8,
∴在Rt△ACE中,由勾股定理，得$AC = \sqrt{AE² + EC²} = \sqrt{4² + 8²} = 4\sqrt{5},$
∴$S△ABE = \frac{1}{2}BE·AE = \frac{1}{2}×3×4 = 6.$点P到达点B的时间$ = \frac{5}{5} = 1($秒),点P到达点E的时间$ = 1 + \frac{3}{2} = \frac{5}{2}($秒),点P到达点C的时间$ = 1 + \frac{11}{2} = \frac{13}{2}($秒),
①如图
(1)，当P在AB上（不含点A,B）运动时，此时0 ＜ t ＜ 1,过点A作AG⊥FP于点G,令AP中点为O.
∵将点E绕PA的中点O旋转180°得到点F,
∴OA = OP,OF = OE,
∴四边形AFPE是平行四边形，

∴FP = AE = 4,FP//AE,
∴∠FPA = ∠BAE,
∴$sin∠FPA = sin∠BAE = \frac{BE}{AB} = \frac{3}{5},$
∴$AG = AP·sin∠FPA = 5t×\frac{3}{5} = 3t,$
∴S四边形AFPE = FP·AG = 12t;
②如图
(2),当P在BE上（含点B）运动时$,1 ≤ t ＜ \frac{5}{2},$
同理可得四边形AFPE是平行四边形，
又AE⊥BE,
∴平行四边形AFPE是矩形.
∵PE = 3 - 2(t - 1) = 5 - 2t,
∴S四边形AFPE = PE·AE = 4(5 - 2t) = -8t + 20;
③如图
(3),当P在EC上（含点C）运动时，$\frac{5}{2} ＜ t ≤ \frac{13}{2},$同理可得四边形AFPE是平行四边形，
又AE⊥BE,
∴▱AFPE是矩形.
∵PE = 2(t - 1) - 3 = 2t - 5,
∴S四边形AFPE = PE·AE = 4(2t - 5) = 8t - 20.
　　　　　　　　12t(0 ＜ t ＜ 1),
综上所述,S四边形$AFPE = \begin{cases} 12t (0 ＜ t ＜ 1), \\ -8t + 20 (1 \leq t ＜ \frac{5}{2}), \\ 8t - 20 (\frac{5}{2} ＜ t \leq \frac{13}{2}). \end{cases}$
　 　　　
(3)①如图
(4),当P在AB上（不含点A,B）运动时，0 ＜ t ＜ 1,
延长CA交FP于点Q,过点A作GA⊥FP,垂足为G，由
(2)可得AG = 3t.
∵PF//AE,AE⊥BC,GA⊥FP,
∴AG//BC,
∴∠B = ∠GAP,∠QAG = ∠C.
∵$tan∠GAP = tanB = \frac{AE}{BE} = \frac{4}{3},tan∠QAG = tanC = \frac{AE}{EC} = \frac{4}{8} = \frac{1}{2},$四边形AFPE是平行四边形，
∴$GP = AG·tan∠PAG = 3t×\frac{4}{3} = 4t,$
$QG = AG·tan∠QAG = \frac{3}{2}t,$
∴$FQ = FP - QG - PG = 4 - 4t - \frac{3}{2}t = 4 - \frac{11}{2}t,$
∴$S△AFQ = \frac{1}{2}FQ·AG = \frac{1}{2}·(4 - \frac{11}{2}t)·3t = \frac{3}{2}·(4 - \frac{11}{2}t)t,$当四边形AFPE被直线AC分得的两部分面积之比为1:3时，即$S△AFQ = \frac{1}{4}S$四边形AFPE或$S△AFQ = \frac{3}{4}S$四边形AFPE,
∴$\frac{3}{2}(4 - \frac{11}{2}t)t = \frac{1}{4}·12t$或$\frac{3}{2}(4 - \frac{11}{2}t)t = \frac{3}{4}·12t,$解得
t1 = 0(舍去$),t2 = \frac{4}{11},t3 = -\frac{4}{11}($负值舍去);
②当P在BE上（含点B）运动时，直线AC不分割四边形AFPE;
③如图
(5),当P在EC上（含点C）运动时，$\frac{5}{2} ≤ t ≤ \frac{13}{2}.$
∵四边形AFPE是矩形，
∴AF = EP = 2t - 5,CP = 11 - 2(t - 1) = 13 - 2t.
∵$PQ = PC·tanC = (13 - 2t)·\frac{1}{2} = \frac{13 - 2t}{2},$
∴$FQ = FP - PQ = 4 - \frac{13 - 2t}{2} = \frac{2t - 5}{2},$
∴$S△AFQ = \frac{1}{2}FQ·AF = \frac{1}{2}·\frac{2t - 5}{2}·(2t - 5) = \frac{1}{4}(2t - 5)²,$
当四边形AFPE被直线AC分得的两部分面积之比为1:3时,即$S△AFQ = \frac{1}{4}S$四边形AFPE或$S△AFQ = \frac{3}{4}S$四边形AFPE,
∴$\frac{1}{4}(2t - 5)² = \frac{1}{4}(8t - 20)$或$\frac{1}{4}(2t - 5)² = \frac{3}{4}(8t - 20),$解得$t1 = \frac{9}{2},t2 = \frac{5}{2}($不合题意舍去$),t3 = \frac{17}{2}($不合题意舍去).综上所述$,t = \frac{4}${1