2025年实验班中考数学压轴题
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班中考数学压轴题 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
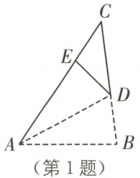
1. (长沙中考)如图,将$ \triangle ABC $沿折痕$ AD $折叠,使点$ B $落在边$ AC $上的点$ E $处,若$ AB = 4 $,$ BC = 5 $,$ AC = 6 $,则$ \triangle CDE $的周长为(
A.$ 5 $
B.$ 6 $
C.$ 6.5 $
D.$ 7 $
D
)。
A.$ 5 $
B.$ 6 $
C.$ 6.5 $
D.$ 7 $
答案:
1.D[解析]
∵AB=4,BC=5,AC=6,
∴由折叠的性质,得AE=AB=4,DE=BD,
∴CE=AC−AE=6−4=2,
CD+DE=CD+BD=BC=5,
∴△CDE的周长为CE+CD+DE=2+5=7.故选D.
∵AB=4,BC=5,AC=6,
∴由折叠的性质,得AE=AB=4,DE=BD,
∴CE=AC−AE=6−4=2,
CD+DE=CD+BD=BC=5,
∴△CDE的周长为CE+CD+DE=2+5=7.故选D.
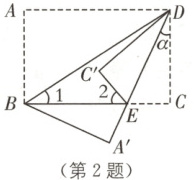
2. (河北中考)如图,将矩形$ ABCD $沿对角线$ BD $折叠,点$ A $落在$ A' $处,$ A'D $交$ BC $于点$ E $。将$ \triangle CDE $沿$ DE $折叠,点$ C $落在$ \triangle BDE $内的$ C' $处,下列结论一定正确的是(
A.$ \angle 1 = 45° - \alpha $
B.$ \angle 1 = \alpha $
C.$ \angle 2 = 90° - \alpha $
D.$ \angle 2 = 2\alpha $
D
)。
A.$ \angle 1 = 45° - \alpha $
B.$ \angle 1 = \alpha $
C.$ \angle 2 = 90° - \alpha $
D.$ \angle 2 = 2\alpha $
答案:
2.D [解析]
∵四边形ABCD是矩形,
∴AD//BC,∠C=90°,
∴∠ADB=∠1.
∵将矩形ABCD沿对角线BD折叠,
∴∠ADB=∠A'DB,
∴∠1=∠A'DB.
∵∠DEC=90°−α,即2∠1=90°−α,
∴∠1=45°−$\frac{1}{2}$α,故A不正确.
∵∠BDE≠∠CDE,
∴∠1≠α,故B不正确.
∵将△CDE 沿DE折叠,
∴∠C'ED=∠CED,∠2=180°−2∠CED=180°−2(90°−α)=2α,故C不正确,D选项正确.故选D.
∵四边形ABCD是矩形,
∴AD//BC,∠C=90°,
∴∠ADB=∠1.
∵将矩形ABCD沿对角线BD折叠,
∴∠ADB=∠A'DB,
∴∠1=∠A'DB.
∵∠DEC=90°−α,即2∠1=90°−α,
∴∠1=45°−$\frac{1}{2}$α,故A不正确.
∵∠BDE≠∠CDE,
∴∠1≠α,故B不正确.
∵将△CDE 沿DE折叠,
∴∠C'ED=∠CED,∠2=180°−2∠CED=180°−2(90°−α)=2α,故C不正确,D选项正确.故选D.
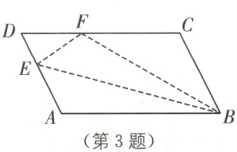
3. 如图,在平行四边形$ ABCD $中,点$ E $在边$ AD $上,以$ BE $为折痕,将$ \triangle ABE $折叠,使点$ A $恰好落在边$ CD $的点$ F $上,若$ \triangle BCF $的周长为$ 12 $,$ CF $的长为$ 3 $,则$ \triangle DEF $的周长为$$
6
$$。
答案:
3.6 [解析]由折叠的性质,得△FBE≌△ABE,
∴BF=AB,EF=AE.
∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC.
∵△BCF的周长为12,
∴BC+BF+CF=12,
∴BC+DC=12−3=9,
∴△DEF的周长=DE+EF+DF=DE+AE+DC−CF=AD+DC−CF=9−3=6.
∴BF=AB,EF=AE.
∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC.
∵△BCF的周长为12,
∴BC+BF+CF=12,
∴BC+DC=12−3=9,
∴△DEF的周长=DE+EF+DF=DE+AE+DC−CF=AD+DC−CF=9−3=6.
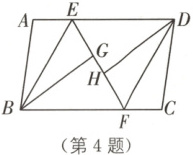
4. 如图,在平行四边形$ ABCD $中,$ E $,$ F $分别在$ AD $,$ BC $上,$ AE = CF $,且$ DE > 2AE $,把$ \triangle ABE $,$ \triangle CDF $分别沿$ BE $,$ DF $折叠,$ A $,$ C $的对应点分别为$ G $,$ H $。若$ E $,$ G $,$ H $,$ F $四点恰好在同一直线上,$ \angle GFB = 60° $,$ GH = 1 $,$ AD = 7 $,则$ AB $的长是$$
√19
$$。
答案:
4. $\sqrt{19}$ [解析]
∵四边形ABCD是平行四边形,
∴AD//BC.由折叠,得GE=AE,HF=CF,∠GEB=∠AEB,∠HFD=∠CFD.
∵AE=CF,
∴GE=HF=AE.
∵E,G,H,F四点在同一直线上,∠GFB=60°,
∴∠DEF=∠GFB=60°,
∴∠GEB=∠AEB=∠HFD=∠CFD=$\frac{1}{2}$×(180°−60°)=60°,
∴∠EBF=∠FDE=60°,
∴△BFE和△DEF都是等边三角形,
∴BE=EF=DE.
∵DE>2AE,GE+HF=2AE,GH=1,
∴EF>GE+HF,
∴BE=DE=EF=GE+HF+GH=2AE+1.
∵AE+DE=AD=7,
∴AE+2AE+1=7,
∴AE=2,
∴BE=5.
如图,作BL⊥DA交DA的延长线于点L,
则∠L=90°,
∴∠EBL=90°−∠AEB=30°,
∴EL=$\frac{1}{2}$BE=$\frac{5}{2}$,
∴AL=EL−AE=$\frac{5}{2}-2=\frac{1}{2}$,
∵$\frac{BL}{EL}$=tan60°=$\sqrt{3}$,
∴BL=$\sqrt{3}$EL=$\frac{5\sqrt{3}}{2}$,
∴AB=$\sqrt{AL^{2}+BL^{2}}=\sqrt{(\frac{1}{2})^{2}+(\frac{5\sqrt{3}}{2})^{2}}=\sqrt{19}$

4. $\sqrt{19}$ [解析]
∵四边形ABCD是平行四边形,
∴AD//BC.由折叠,得GE=AE,HF=CF,∠GEB=∠AEB,∠HFD=∠CFD.
∵AE=CF,
∴GE=HF=AE.
∵E,G,H,F四点在同一直线上,∠GFB=60°,
∴∠DEF=∠GFB=60°,
∴∠GEB=∠AEB=∠HFD=∠CFD=$\frac{1}{2}$×(180°−60°)=60°,
∴∠EBF=∠FDE=60°,
∴△BFE和△DEF都是等边三角形,
∴BE=EF=DE.
∵DE>2AE,GE+HF=2AE,GH=1,
∴EF>GE+HF,
∴BE=DE=EF=GE+HF+GH=2AE+1.
∵AE+DE=AD=7,
∴AE+2AE+1=7,
∴AE=2,
∴BE=5.
如图,作BL⊥DA交DA的延长线于点L,
则∠L=90°,
∴∠EBL=90°−∠AEB=30°,
∴EL=$\frac{1}{2}$BE=$\frac{5}{2}$,
∴AL=EL−AE=$\frac{5}{2}-2=\frac{1}{2}$,
∵$\frac{BL}{EL}$=tan60°=$\sqrt{3}$,
∴BL=$\sqrt{3}$EL=$\frac{5\sqrt{3}}{2}$,
∴AB=$\sqrt{AL^{2}+BL^{2}}=\sqrt{(\frac{1}{2})^{2}+(\frac{5\sqrt{3}}{2})^{2}}=\sqrt{19}$

5. 如图,在扇形$ OAB $中,$ \angle AOB = 90° $,$ OA = 6 $,将扇形$ OAB $沿过点$ B $的直线折叠,点$ O $恰好落在$ AB $上的点$ D $处,折痕交$ OA $于点$ C $,则整个阴影部分的面积为(
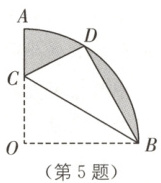
A.$ 9\pi - 9\sqrt{3} $
B.$ 9\pi - 6\sqrt{3} $
C.$ 6\pi - 9\sqrt{3} $
D.$ 9\pi - 12\sqrt{3} $
D
)。
A.$ 9\pi - 9\sqrt{3} $
B.$ 9\pi - 6\sqrt{3} $
C.$ 6\pi - 9\sqrt{3} $
D.$ 9\pi - 12\sqrt{3} $
答案:
5.D [解析]如图,连接OD.
根据折叠的性质,得CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,即△OBD是等边三角形,
∴∠DBO=60°,
∴∠CBO=$\frac{1}{2}$∠DBO=30°.
∵∠AOB=90°,
∴OC=OB·tan∠CBO =6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
∴S△BDC=S△OBC=$\frac{1}{2}$OB·OC=$\frac{1}{2}$×6×2$\sqrt{3}$=6$\sqrt{3}$,S扇形OAB=$\frac{90\pi×6^{2}}{360}$=9π,
∴整个阴影部分的面积为S扇形OAB−S△BDC−S△OBC=9π−6$\sqrt{3}$−6$\sqrt{3}$=9π−12$\sqrt{3}$.故选D.

5.D [解析]如图,连接OD.
根据折叠的性质,得CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,即△OBD是等边三角形,
∴∠DBO=60°,
∴∠CBO=$\frac{1}{2}$∠DBO=30°.
∵∠AOB=90°,
∴OC=OB·tan∠CBO =6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
∴S△BDC=S△OBC=$\frac{1}{2}$OB·OC=$\frac{1}{2}$×6×2$\sqrt{3}$=6$\sqrt{3}$,S扇形OAB=$\frac{90\pi×6^{2}}{360}$=9π,
∴整个阴影部分的面积为S扇形OAB−S△BDC−S△OBC=9π−6$\sqrt{3}$−6$\sqrt{3}$=9π−12$\sqrt{3}$.故选D.

6. (无锡二模)如图,在矩形纸片$ ABCD $中,$ AB = 6 $,$ BC = 8 $。把$ \triangle BCD $沿对角线$ BD $折叠,使点$ C $落在$ C' $处,$ BC' $交$ AD $于点$ G $,交$ AF $于点$ M $;$ E $,$ F $分别是$ C'D $和$ BD $上的点,线段$ EF $交$ AD $于点$ H $,把$ \triangle FDE $沿$ EF $折叠,使点$ D $落在$ D' $处,点$ D' $恰好与点$ A $重合。下列选项:①$ \triangle ABG \cong \triangle C'DG $;②$ \tan \angle ABG = \frac{7}{24} $;③$ EF = \frac{7}{6} $;④$ AM : FM = \frac{14}{25} $。其中正确的是(
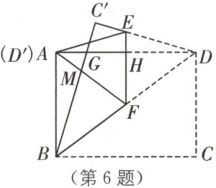
A.①②③④
B.①②④
C.②③④
D.①③④
B
)。
A.①②③④
B.①②④
C.②③④
D.①③④
答案:
6.B [解析]
∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=8,∠BAG=∠C=90°.由折叠,可得CD=C'D=6,∠BC'D=∠C=90°,
∴AB=C'D,∠BAG=∠DC'G.又∠AGB=∠C'GD,
∴△ABG≌△C'DG (AAS),故①正确;
∵△ABG≌△C'DG,
∴BG=DG.设AG=x,则BG=DG=8−x.在Rt△ABG中,AB²+AG²=BG²,
∴6²+x²=(8−x)²,解得x=$\frac{7}{4}$,
∴AG=$\frac{7}{4}$,tan∠ABG=$\frac{AG}{AB}$=$\frac{\frac{7}{4}}{6}$=$\frac{7}{24}$,故②正确;由折叠,可得DH=AH=$\frac{1}{2}$AD=4,EF⊥AD,
∴∠DHE=∠DHF=90°,∠DHE=∠C'=90°,∠HDE=∠C'DG,
∴△HDE∽△C'DG,
∴C'G=AG=$\frac{7}{4}$,
∴$\frac{HE}{C'G}$=$\frac{DH}{DC'}$,即$\frac{HE}{\frac{7}{4}}$=$\frac{4}{6}$,HE=$\frac{7}{6}$,∠DHF=∠DAB=90°,
∴HF//AB,
∴△DHF∽△DAB,
∴$\frac{HF}{AB}$=$\frac{DH}{DA}$=$\frac{1}{2}$,
∴HF=$\frac{1}{2}$AB=3,EF=HE+HF=$\frac{7}{6}$+3=$\frac{25}{6}$,故③错误;如图,延长EF交BC于点I,延长FE交BC'的延长线于点N.
∵AD//BC,
∴△NGH∽△NBI,
∴$\frac{GH}{BI}$=$\frac{NH}{NI}$.
∵∠BAH=∠AHI=∠ABI=90°,
∴四边形ABIH是矩形,
∴BI=AH=4,HI=AB=6.
∵AH//BI,AG=$\frac{7}{4}$,
∴GH=AH−AG=4−$\frac{7}{4}$=$\frac{9}{4}$,
∴$\frac{\frac{9}{4}}{4}$=$\frac{NH}{NH+6}$,解得NH=$\frac{54}{7}$.
∵HF=3,
∴NF=NH+HF=$\frac{54}{7}$+3=$\frac{75}{7}$.
∵AB//NF,
∴△ABM∽△FNM,
∴$\frac{AM}{FM}$=$\frac{AB}{FN}$=$\frac{6}{\frac{75}{7}}$=$\frac{14}{25}$,故④正确.
综上,正确的是①②④.故选B

6.B [解析]
∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=8,∠BAG=∠C=90°.由折叠,可得CD=C'D=6,∠BC'D=∠C=90°,
∴AB=C'D,∠BAG=∠DC'G.又∠AGB=∠C'GD,
∴△ABG≌△C'DG (AAS),故①正确;
∵△ABG≌△C'DG,
∴BG=DG.设AG=x,则BG=DG=8−x.在Rt△ABG中,AB²+AG²=BG²,
∴6²+x²=(8−x)²,解得x=$\frac{7}{4}$,
∴AG=$\frac{7}{4}$,tan∠ABG=$\frac{AG}{AB}$=$\frac{\frac{7}{4}}{6}$=$\frac{7}{24}$,故②正确;由折叠,可得DH=AH=$\frac{1}{2}$AD=4,EF⊥AD,
∴∠DHE=∠DHF=90°,∠DHE=∠C'=90°,∠HDE=∠C'DG,
∴△HDE∽△C'DG,
∴C'G=AG=$\frac{7}{4}$,
∴$\frac{HE}{C'G}$=$\frac{DH}{DC'}$,即$\frac{HE}{\frac{7}{4}}$=$\frac{4}{6}$,HE=$\frac{7}{6}$,∠DHF=∠DAB=90°,
∴HF//AB,
∴△DHF∽△DAB,
∴$\frac{HF}{AB}$=$\frac{DH}{DA}$=$\frac{1}{2}$,
∴HF=$\frac{1}{2}$AB=3,EF=HE+HF=$\frac{7}{6}$+3=$\frac{25}{6}$,故③错误;如图,延长EF交BC于点I,延长FE交BC'的延长线于点N.
∵AD//BC,
∴△NGH∽△NBI,
∴$\frac{GH}{BI}$=$\frac{NH}{NI}$.
∵∠BAH=∠AHI=∠ABI=90°,
∴四边形ABIH是矩形,
∴BI=AH=4,HI=AB=6.
∵AH//BI,AG=$\frac{7}{4}$,
∴GH=AH−AG=4−$\frac{7}{4}$=$\frac{9}{4}$,
∴$\frac{\frac{9}{4}}{4}$=$\frac{NH}{NH+6}$,解得NH=$\frac{54}{7}$.
∵HF=3,
∴NF=NH+HF=$\frac{54}{7}$+3=$\frac{75}{7}$.
∵AB//NF,
∴△ABM∽△FNM,
∴$\frac{AM}{FM}$=$\frac{AB}{FN}$=$\frac{6}{\frac{75}{7}}$=$\frac{14}{25}$,故④正确.
综上,正确的是①②④.故选B

7. (苏州二模)如图,在矩形$ ABCD $中,$ AB = 6 $,$ AD = 8 $,$ E $,$ F $分别是$ BC $,$ CD $上的一点,$ EF \perp AE $,将$ \triangle ECF $沿$ EF $翻折得到$ \triangle EC'F $,连接$ AC' $。若$ \triangle AEC' $是以$ AE $为腰的等腰三角形,则$ BE = $
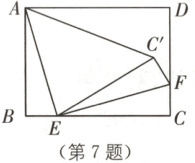
7/4或8/3
$ $。
答案:
7.$\frac{7}{4}$或$\frac{8}{3}$ [解析]在长方形ABCD中,AB=6,AD=8,设BE=x,则EC=8−x.
∵将△ECF沿EF翻折得到△EC'F,
∴EC'=EC=8−x,当AE=EC'时,AE=8−x.
∵四边形ABCD为矩形,
∴∠B=90°,在直角三角形ABE中,由勾股定理,得6²+x²=(8−x)²,解得x=$\frac{7}{4}$.当AE=AC'时.如图,作AH⊥EC'.
∵EF⊥AE,
∴∠AEF=∠AEC'+∠FEC'=90°,
∴∠BEA+∠FEC=90°.
∵△ECF沿EF翻折得到△EC'F,
∴∠FEC'=∠FEC,
∴∠AEB=∠AEH.
∵∠B=∠AHE,
在△ABE和△AHE中,$\begin{cases}\angle B=\angle AHE\\\angle AEB=\angle AEH\\AE=AE\end{cases}$
∴△ABE≌△AHE(AAS),
∴BE=HE=x.
∵AE=AC',
∴EC'=2EH,即8−x=2x,解得x=$\frac{8}{3}$.
综上所述,BE=$\frac{7}{4}$或$\frac{8}{3}$.

7.$\frac{7}{4}$或$\frac{8}{3}$ [解析]在长方形ABCD中,AB=6,AD=8,设BE=x,则EC=8−x.
∵将△ECF沿EF翻折得到△EC'F,
∴EC'=EC=8−x,当AE=EC'时,AE=8−x.
∵四边形ABCD为矩形,
∴∠B=90°,在直角三角形ABE中,由勾股定理,得6²+x²=(8−x)²,解得x=$\frac{7}{4}$.当AE=AC'时.如图,作AH⊥EC'.
∵EF⊥AE,
∴∠AEF=∠AEC'+∠FEC'=90°,
∴∠BEA+∠FEC=90°.
∵△ECF沿EF翻折得到△EC'F,
∴∠FEC'=∠FEC,
∴∠AEB=∠AEH.
∵∠B=∠AHE,
在△ABE和△AHE中,$\begin{cases}\angle B=\angle AHE\\\angle AEB=\angle AEH\\AE=AE\end{cases}$
∴△ABE≌△AHE(AAS),
∴BE=HE=x.
∵AE=AC',
∴EC'=2EH,即8−x=2x,解得x=$\frac{8}{3}$.
综上所述,BE=$\frac{7}{4}$或$\frac{8}{3}$.

8. (武汉模拟)如图,已知在$ \triangle ABC $中,$ \angle ACB = 90° $,$ AC = 2 $,$ BC = 4 $,点$ E $为$ AB $的中点,$ D $为边$ BC $上的一动点,把$ \triangle ACD $沿$ AD $折叠,点$ C $落在点$ F $处,当$ \triangle AEF $为直角三角形时,$ CD $的长为$$
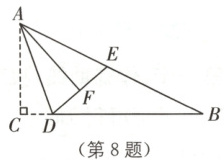
2或2/3
$$。
答案:
8.2或$\frac{2}{3}$ [解析]如图
(1),当∠AFE=90°时,过点E作EM⊥BC,垂足为M,过点A作AN⊥ME交ME延长线于点N.
∵∠C=∠EMB=90°,
∴EM//AC,
∴$\frac{AE}{BE}$=$\frac{CM}{BM}$.
∵AE=EB,
∴MB=MC=$\frac{1}{2}$BC=2,
∴EM=$\frac{1}{2}$AC=1.
∵∠C=∠CMN=∠N=90°,
∴四边形ACMN是矩形.
∵AC=CM=2,
∴四边形ACMN是正方形.在Rt△ABC 中,AC=2,BC=4,
∴AB=$\sqrt{AC^{2}+BC^{2}}$=$\sqrt{4+16}$=2$\sqrt{5}$,AE=$\sqrt{5}$.在Rt△AFE中,
∵AE=$\sqrt{5}$,AF=AC=2,
∴FE=$\sqrt{AE^{2}-AF^{2}}$=$\sqrt{5−4}$=1.设CD=FD=x,在Rt△EDM中,DE=1+x,EM=1,DM=2−x,
∴DE²=DM²+EM²,
∴(1+x)²=(2−x)²+1²,
∴x=$\frac{2}{3}$,
∴CD=$\frac{2}{3}$;
如图
(2),当∠AFE=90°时,
∵∠AFD=90°,
∴F,E,D共线.
在Rt△AFE中,AE=$\sqrt{5}$,AF=AC=2,
∴EF=$\sqrt{AE^{2}-AF^{2}}$=$\sqrt{5−4}$=1,
∴$\frac{AF}{BC}$=$\frac{EF}{AC}$=$\frac{1}{2}$.
∵∠C=∠F,
∴△AFE∽△BCA,
∴∠FAE=∠B.
∵AE=EB,∠AEF=∠BED,∠FAE=∠B,
∴△AFE≌△BDE(ASA),
∴∠BDE=∠F=90°.
∵∠C=∠F=∠CDF=90°,
∴四边形ACDF是矩形.
∵AC=AF,
∴四边形ACDF是正方形,
∴CD=AC=2.综上所述,CD=2或$\frac{2}{3}$.

8.2或$\frac{2}{3}$ [解析]如图
(1),当∠AFE=90°时,过点E作EM⊥BC,垂足为M,过点A作AN⊥ME交ME延长线于点N.
∵∠C=∠EMB=90°,
∴EM//AC,
∴$\frac{AE}{BE}$=$\frac{CM}{BM}$.
∵AE=EB,
∴MB=MC=$\frac{1}{2}$BC=2,
∴EM=$\frac{1}{2}$AC=1.
∵∠C=∠CMN=∠N=90°,
∴四边形ACMN是矩形.
∵AC=CM=2,
∴四边形ACMN是正方形.在Rt△ABC 中,AC=2,BC=4,
∴AB=$\sqrt{AC^{2}+BC^{2}}$=$\sqrt{4+16}$=2$\sqrt{5}$,AE=$\sqrt{5}$.在Rt△AFE中,
∵AE=$\sqrt{5}$,AF=AC=2,
∴FE=$\sqrt{AE^{2}-AF^{2}}$=$\sqrt{5−4}$=1.设CD=FD=x,在Rt△EDM中,DE=1+x,EM=1,DM=2−x,
∴DE²=DM²+EM²,
∴(1+x)²=(2−x)²+1²,
∴x=$\frac{2}{3}$,
∴CD=$\frac{2}{3}$;
如图
(2),当∠AFE=90°时,
∵∠AFD=90°,
∴F,E,D共线.
在Rt△AFE中,AE=$\sqrt{5}$,AF=AC=2,
∴EF=$\sqrt{AE^{2}-AF^{2}}$=$\sqrt{5−4}$=1,
∴$\frac{AF}{BC}$=$\frac{EF}{AC}$=$\frac{1}{2}$.
∵∠C=∠F,
∴△AFE∽△BCA,
∴∠FAE=∠B.
∵AE=EB,∠AEF=∠BED,∠FAE=∠B,
∴△AFE≌△BDE(ASA),
∴∠BDE=∠F=90°.
∵∠C=∠F=∠CDF=90°,
∴四边形ACDF是矩形.
∵AC=AF,
∴四边形ACDF是正方形,
∴CD=AC=2.综上所述,CD=2或$\frac{2}{3}$.

查看更多完整答案,请扫码查看


