《2025年教与学课程同步讲练九年级数学全一册浙教版》

例1 下列说法中,正确的是 (D)
A. 弦是直径
B. 长度相等的弧是等弧
C. 半圆是圆中最长的弧
D. 直径是圆中最长的弦

答案： 【解析】：
本题主要考察对圆的基本概念的理解，包括弦、直径、弧等定义及其性质。
A选项错误，因为弦是连接圆上任意两点的线段，而直径是特殊的弦，它通过圆心，但并非所有弦都是直径。
B选项错误，因为等弧的定义是在同圆或等圆中，能够互相重合的弧。仅仅长度相等并不能判定为等弧。
C选项错误，因为优弧是大于半圆的弧，所以半圆并不是圆中最长的弧。
D选项正确，因为在圆中，直径是穿过圆心的弦，其长度等于圆的直径，因此它是圆中最长的弦。
【答案】：
D

例2 如图 3-1-1,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= 2\ \text{cm}$,$BC= 4\ \text{cm}$,CM 是中线,以点 C 为圆心,$\sqrt{5}\ \text{cm}$为半径画圆,请判断点 A,B,M 与$\odot C$的位置关系.

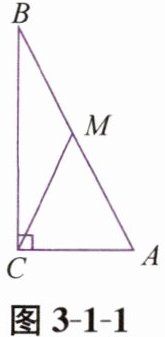
答案： 【解析】：本题主要考查点和圆的位置关系，通过比较点到圆心的距离$d$与圆半径$r$的大小关系来判断：当$d\lt r$时，点在圆内；当$d = r$时，点在圆上；当$d\gt r$时，点在圆外。
已知在$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AC = 2\text{cm}$，$BC = 4\text{cm}$，$CM$是中线，以$C$为圆心，$\sqrt{5}\text{cm}$为半径画圆。
先根据勾股定理求出斜边$AB$的长度，再根据直角三角形斜边中线定理求出$CM$的长度，最后分别比较$CA$、$CB$、$CM$与圆半径$\sqrt{5}\text{cm}$的大小关系，从而判断点$A$、$B$、$M$与圆$\odot C$的位置关系。
【答案】：解：
由勾股定理，在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AC = 2\text{cm}$，$BC = 4\text{cm}$，
可得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{2^{2} + 4^{2}}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}(\text{cm})$。
因为$\angle ACB = 90^{\circ}$，$CM$是中线，根据直角三角形斜边中线定理：直角三角形斜边的中线等于斜边的一半，
所以$CM=\frac{1}{2}AB=\sqrt{5}(\text{cm})$。
比较$CA$与圆半径$r = \sqrt{5}\text{cm}$的大小：
已知$CA = 2\text{cm}$，$2\lt\sqrt{5}$，即$CA\lt r$，
所以点$A$在$\odot C$内。
比较$CB$与圆半径$r = \sqrt{5}\text{cm}$的大小：
已知$CB = 4\text{cm}$，$4\gt\sqrt{5}$，即$CB\gt r$，
所以点$B$在$\odot C$外。
比较$CM$与圆半径$r = \sqrt{5}\text{cm}$的大小：
因为$CM=\sqrt{5}\text{cm}$，即$CM = r$，
所以点$M$在$\odot C$上。
综上，点$A$在$\odot C$内，点$B$在$\odot C$外，点$M$在$\odot C$上。