《2025年教与学课程同步讲练九年级数学全一册浙教版》

9. 如图，在$3×3$的正方形网格的格点上摆放了两枚棋子，第三枚棋子随机摆放在格点上（每个格点处最多摆放一枚），这三枚棋子所在格点恰好是等腰三角形顶点的概率是（ ）


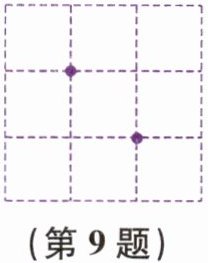
A.$\frac{2}{7}$
B.$\frac{1}{3}$
C.$\frac{4}{7}$
D.$\frac{2}{3}$

答案：
C[画树状图如解图所示.　 由树状图可知，$P(Q_{2})=P(Q_{9})=\frac{1}{20}$，$P(Q_{3})=P(Q_{8})=\frac{2}{20}=\frac{1}{10}$，$P(Q_{4})=P(Q_{7})=\frac{3}{20}$，$P(Q_{5})=P(Q_{6})=\frac{4}{20}=\frac{1}{5}$，$\therefore$当$Q_{n}$的概率最大时，$n$的值为5或6.]

10. 已知$M(a,b)$是平面直角坐标系中的点，其中a是从1，2，3，4四个数中任取的一个数，b是从1，2，3，4，5五个数中任取的一个数. 定义“点$M(a,b)$在直线$x+y=n$上”为事件$Q_n(2 \leq n \leq 9$，n为整数)，则当$Q_n$的概率最大时，n的值为（C）
A.5
B.4或5
C.5或6
D.6或7

答案： 【解析】：
首先，点$M(a,b)$的坐标$a$有4种可能的取值（1,2,3,4），坐标$b$有5种可能的取值（1,2,3,4,5）。
因此，点$M(a,b)$的所有可能组合为$4 × 5 = 20$种。
接下来，我们需要找出使得事件$Q_n$（即点$M(a,b)$在直线$x+y=n$上）的概率最大的$n$值。
对于每一个可能的$n$值（$2 \leq n \leq 9$），我们需要计算满足$a+b=n$的$(a,b)$组合的数量。
当$n=2$时，只有$(1,1)$满足条件，概率为$\frac{1}{20}$。
当$n=3$时，有$(1,2),(2,1)$满足条件，概率为$\frac{2}{20}$。
当$n=4$时，有$(1,3),(2,2),(3,1)$满足条件，概率为$\frac{3}{20}$。
当$n=5$时，有$(1,4),(2,3),(3,2),(4,1)$满足条件，概率为$\frac{4}{20} = \frac{1}{5}$。
当$n=6$时，有$(1,5),(2,4),(3,3),(4,2)$满足条件，概率为$\frac{4}{20} = \frac{1}{5}$（与$n=5$时相同）。
当$n=7$时，有$(2,5),(3,4),(4,3)$满足条件，概率为$\frac{3}{20}$。
当$n=8$时，有$(3,5),(4,4)$满足条件，概率为$\frac{2}{20}$。
当$n=9$时，只有$(4,5)$满足条件，概率为$\frac{1}{20}$。
由此可见，当$n=5$或$n=6$时，事件$Q_n$的概率最大，为$\frac{1}{5}$。
【答案】：
C

11. 一个不透明的袋子中装有2个红球、5个白球和3个黑球，这些球除颜色外都相同. 从袋子中任意摸出1个球，摸到白（填“红”“白”或“黑”）球的可能性最大.

答案： 白

12. 有8张卡片，上面分别写着数1，2,3,4,5,6,7,8.从中随机抽取1张，该卡片上的数据数是4 的整数倍概率是的概率$\frac{1}{4}$.

答案： $\frac{1}{4}$

13..一个仅装有球的不透明布袋里有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球概率是的概率是$\frac{2}{5}$,则n的值为9.

答案： 9

14. 口袋中有10个球（每个球除颜色外都相同），其中白球x个，红球2x个其余为蓝球.从袋从中随机摸出一个球摸到红球则甲获胜摸到蓝球则乙获胜..要使游戏对甲、乙双方公平，则x应该等于______2.

答案： 2

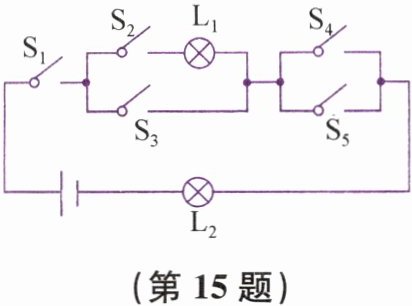
15..如图随机闭合开关$S_1,S_2,S_3,S_4,S_5$中的三个能够使灯泡$L_1,L_2$同时发光的概率是$\frac{1}{5}$.

答案： $\frac{1}{5}$

16. 有形状、大小一样，背面相同的四张卡片，其中三张卡片正面分别标有数字2，3，4，小明随机抽一张记下数字后放回，混合均匀，小亮再随机抽一张记下数字. 如果两人记下的数字之和是8的概率是$\frac{3}{16}$，那么第四张卡片正面标的数字是______.

答案：
5或6[设第四张卡片正面标的数字为$x$，则画树状图如解图所示.　 当$2+x=8$，即$x=6$时，和为8的结果有3种，即$P=\frac{3}{16}$，符合题意；当$3+x=8$，即$x=5$时，和为8的结果有3种，即$P=\frac{3}{16}$，符合题意；当$4+x=8$，即$x=4$时，和为8的结果有4种，即$P=\frac{4}{16}=\frac{1}{4}$，不符合题意. 综上所述，第四张卡片正面标的数字是5或6.]

17. (8分)有两枚质地均匀的骰子，同时抛掷一次，将两个朝上的面所示的点数相加，请判断下列事件是什么事件，并说明理由.①和为1；②和为9；③和小于13.

答案： ①是不可能事件，②是随机事件，③是必然事件，理由略