第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
9. 在一个不透明的盒子里装有黑、白两种颜色的球共100个,这些球除颜色外其余完全相同. 小颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
|摸球的次数n|100|200|500|800|1000|3000|
|----|----|----|----|----|----|----|
|摸到白球的次数m|70|124|325|538|670|2004|
|摸到白球的频率$\frac{m}{n}$|0.70|0.62|0.65|0.6725|0.670|0.668|
(1)若从盒子里随机摸出一个球,则估计摸到白球的概率是
(2)估计盒子里黑球有
(3)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是
A. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
B. 掷一枚质地均匀的硬币,落地时结果是“反面朝上”
C. 掷一枚质地均匀的正方体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5
|摸球的次数n|100|200|500|800|1000|3000|
|----|----|----|----|----|----|----|
|摸到白球的次数m|70|124|325|538|670|2004|
|摸到白球的频率$\frac{m}{n}$|0.70|0.62|0.65|0.6725|0.670|0.668|
(1)若从盒子里随机摸出一个球,则估计摸到白球的概率是
0.67
(精确到0.01).(2)估计盒子里黑球有
33
个.(3)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是
C
(填字母).A. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
B. 掷一枚质地均匀的硬币,落地时结果是“反面朝上”
C. 掷一枚质地均匀的正方体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5
答案:
1. (1)
当试验次数很大时,频率稳定于概率,从表格中可以看出,随着摸球次数$n$的增大,摸到白球的频率$\frac{m}{n}$稳定在$0.67$左右(精确到$0.01$)。
所以估计摸到白球的概率$P = 0.67$。
2. (2)
已知球的总数是$n = 100$个,设白球有$x$个,由(1)知摸到白球的概率$P=\frac{x}{100}=0.67$,则白球个数$x = 100×0.67 = 67$个。
那么黑球个数$y=100 - 67=33$个。
3. (3)
选项A:一副扑克牌(去掉大小王)共$52$张,红色牌(红桃和方块)有$26$张,从一副扑克牌(去掉大小王)中任意抽取一张,这张牌是“红色的”概率$P=\frac{26}{52}=0.5$;若算上大小王共$54$张牌,红色牌$26$张,概率$P=\frac{26}{54}\approx0.48$。
选项B:掷一枚质地均匀的硬币,落地时结果是“反面朝上”的概率$P=\frac{1}{2}=0.5$。
选项C:掷一枚质地均匀的正方体骰子(面的点数标记分别为$1$到$6$),落地时面朝上的点数小于$5$(即点数为$1$,$2$,$3$,$4$)的概率$P=\frac{4}{6}=\frac{2}{3}\approx0.67$。
故答案依次为:(1)$0.67$;(2)$33$;(3)C。
当试验次数很大时,频率稳定于概率,从表格中可以看出,随着摸球次数$n$的增大,摸到白球的频率$\frac{m}{n}$稳定在$0.67$左右(精确到$0.01$)。
所以估计摸到白球的概率$P = 0.67$。
2. (2)
已知球的总数是$n = 100$个,设白球有$x$个,由(1)知摸到白球的概率$P=\frac{x}{100}=0.67$,则白球个数$x = 100×0.67 = 67$个。
那么黑球个数$y=100 - 67=33$个。
3. (3)
选项A:一副扑克牌(去掉大小王)共$52$张,红色牌(红桃和方块)有$26$张,从一副扑克牌(去掉大小王)中任意抽取一张,这张牌是“红色的”概率$P=\frac{26}{52}=0.5$;若算上大小王共$54$张牌,红色牌$26$张,概率$P=\frac{26}{54}\approx0.48$。
选项B:掷一枚质地均匀的硬币,落地时结果是“反面朝上”的概率$P=\frac{1}{2}=0.5$。
选项C:掷一枚质地均匀的正方体骰子(面的点数标记分别为$1$到$6$),落地时面朝上的点数小于$5$(即点数为$1$,$2$,$3$,$4$)的概率$P=\frac{4}{6}=\frac{2}{3}\approx0.67$。
故答案依次为:(1)$0.67$;(2)$33$;(3)C。
10. 一只不透明的袋子中装有红、白两种颜色的小球共10个,每次从袋子中摸出1个球,然后放回搅匀后再摸. 在摸球试验中得到下列表中部分数据(频率精确到0.01):
|摸球次数|200| |600| | |1200|
|----|----|----|----|----|----|----|
|出现红球的频数| |180| |336| |480|
|出现红球的频率| |0.45| |0.41| | |
|出现白球的频数| | |360|590| | |
|出现白球的频率|0.57| | | | | |
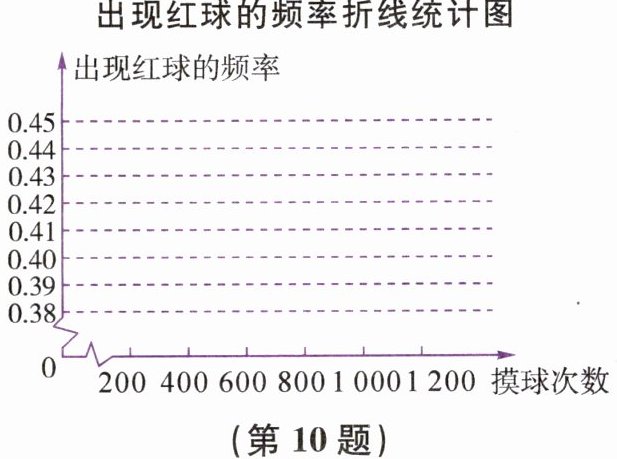
(1)请将表中的数据填写完整.
(2)在图中画出出现红球的频率折线统计图.
(3)观察图表,出现红球的概率约是 ,出现白球的概率约是 .
(4)要使摸到红球的概率是$\frac{3}{5}$,则需再放入几个红球?
|摸球次数|200| |600| | |1200|
|----|----|----|----|----|----|----|
|出现红球的频数| |180| |336| |480|
|出现红球的频率| |0.45| |0.41| | |
|出现白球的频数| | |360|590| | |
|出现白球的频率|0.57| | | | | |

(1)请将表中的数据填写完整.
(2)在图中画出出现红球的频率折线统计图.
(3)观察图表,出现红球的概率约是 ,出现白球的概率约是 .
(4)要使摸到红球的概率是$\frac{3}{5}$,则需再放入几个红球?
答案:
(1)补充数据如下表:

(2)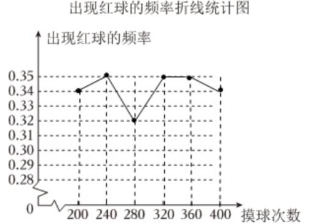
(3)0.40 0.60
(4)由
(3)可知,出现红球的概率约是 0.40,
∴原来袋中有红球 $10×0.40=4$(个).设需再放入x个红球,则 $\frac{4+x}{10+x}=\frac{3}{5}$,解得$x=5$,
∴需再放入5个红球.
(1)补充数据如下表:

(2)

(3)0.40 0.60
(4)由
(3)可知,出现红球的概率约是 0.40,
∴原来袋中有红球 $10×0.40=4$(个).设需再放入x个红球,则 $\frac{4+x}{10+x}=\frac{3}{5}$,解得$x=5$,
∴需再放入5个红球.
查看更多完整答案,请扫码查看


