第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
变式3 根据以下素材,完成探索任务.
|素材1|如图①,△ABC是腰长为60cm的等腰直角三角形卡纸,甲、乙、丙三名同学分别用这样的卡纸尝试裁剪出不一样的矩形纸片.|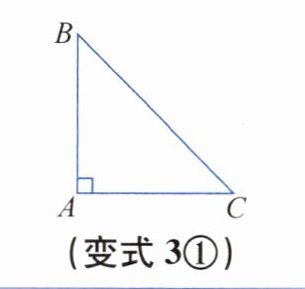
|
|素材2|甲同学按如图②所示的方式裁剪,想裁出面积为800cm²的矩形纸片,乙同学按如图③所示的方式裁剪,想裁出两边长之比为1:2的矩形纸片,丙同学想裁出面积最大的矩形纸片.|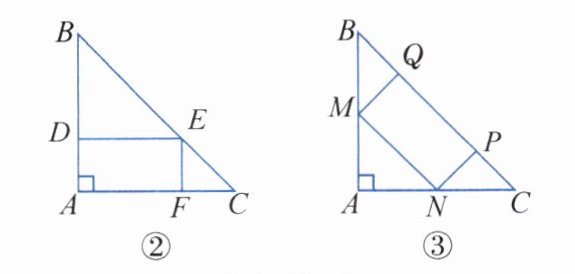
|
|问题解决|
|任务1|请帮甲同学计算出符合要求的矩形纸片的两边长.|
|任务2|请求出符合乙同学裁剪方案的矩形纸片的面积.|
|任务3|请帮丙同学计算出面积最大的矩形纸片的面积.|
|素材1|如图①,△ABC是腰长为60cm的等腰直角三角形卡纸,甲、乙、丙三名同学分别用这样的卡纸尝试裁剪出不一样的矩形纸片.|

|
|素材2|甲同学按如图②所示的方式裁剪,想裁出面积为800cm²的矩形纸片,乙同学按如图③所示的方式裁剪,想裁出两边长之比为1:2的矩形纸片,丙同学想裁出面积最大的矩形纸片.|

|
|问题解决|
|任务1|请帮甲同学计算出符合要求的矩形纸片的两边长.|
|任务2|请求出符合乙同学裁剪方案的矩形纸片的面积.|
|任务3|请帮丙同学计算出面积最大的矩形纸片的面积.|
答案:
任务1
解:设$AD = x\mathrm{cm}$,则$DE = x\mathrm{cm}$,$FC = x\mathrm{cm}$,$DF=(60 - x)\mathrm{cm}$。
根据矩形面积公式$S = 长×宽$,可得$x(60 - x)=800$。
即$x^{2}-60x + 800 = 0$,对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,这里$a = 1$,$b=-60$,$c = 800$,由求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$可得:
$x=\frac{60\pm\sqrt{(-60)^{2}-4×1×800}}{2×1}=\frac{60\pm\sqrt{3600 - 3200}}{2}=\frac{60\pm\sqrt{400}}{2}=\frac{60\pm20}{2}$。
解得$x_{1}=20$,$x_{2}=40$。
当$x = 20$时,$60 - x=40$;当$x = 40$时,$60 - x = 20$。
所以矩形纸片的两边长分别为$20\mathrm{cm}$和$40\mathrm{cm}$。
任务2
解:设$MN = y\mathrm{cm}$,则$MQ = 2y\mathrm{cm}$。
因为$\triangle BMQ$和$\triangle ABC$相似,$\triangle ABC$是等腰直角三角形,$\angle BAC=90^{\circ}$,$AB = AC = 60\mathrm{cm}$。
$\triangle BMQ$也是等腰直角三角形,则$AQ = MQ = 2y\mathrm{cm}$,$AN = y\mathrm{cm}$。
由$AQ+AN=60$,即$2y + y=60$,解得$y = 20$。
所以$MN = 20\mathrm{cm}$,$MQ = 40\mathrm{cm}$。
根据矩形面积公式$S = MN× MQ$,可得矩形面积$S=20×40 = 800\mathrm{cm}^{2}$。
任务3
解:设$AD = m\mathrm{cm}$,则$DE = m\mathrm{cm}$,$FC = m\mathrm{cm}$,$DF=(60 - m)\mathrm{cm}$。
矩形面积$S=m(60 - m)=-m^{2}+60m$。
对于二次函数$y = ax^{2}+bx + c(a\neq0)$,这里$a=-1$,$b = 60$,$c = 0$,其对称轴为$x=-\frac{b}{2a}=-\frac{60}{2×(-1)} = 30$。
因为$a=-1\lt0$,所以当$m = 30$时,$S$有最大值。
$S_{max}=-30^{2}+60×30=-900 + 1800=900\mathrm{cm}^{2}$。
所以面积最大的矩形纸片的面积是$900\mathrm{cm}^{2}$。
综上,任务1答案为$\boldsymbol{20\mathrm{cm}}$和$\boldsymbol{40\mathrm{cm}}$;任务2答案为$\boldsymbol{800\mathrm{cm}^{2}}$;任务3答案为$\boldsymbol{900\mathrm{cm}^{2}}$。
解:设$AD = x\mathrm{cm}$,则$DE = x\mathrm{cm}$,$FC = x\mathrm{cm}$,$DF=(60 - x)\mathrm{cm}$。
根据矩形面积公式$S = 长×宽$,可得$x(60 - x)=800$。
即$x^{2}-60x + 800 = 0$,对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,这里$a = 1$,$b=-60$,$c = 800$,由求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$可得:
$x=\frac{60\pm\sqrt{(-60)^{2}-4×1×800}}{2×1}=\frac{60\pm\sqrt{3600 - 3200}}{2}=\frac{60\pm\sqrt{400}}{2}=\frac{60\pm20}{2}$。
解得$x_{1}=20$,$x_{2}=40$。
当$x = 20$时,$60 - x=40$;当$x = 40$时,$60 - x = 20$。
所以矩形纸片的两边长分别为$20\mathrm{cm}$和$40\mathrm{cm}$。
任务2
解:设$MN = y\mathrm{cm}$,则$MQ = 2y\mathrm{cm}$。
因为$\triangle BMQ$和$\triangle ABC$相似,$\triangle ABC$是等腰直角三角形,$\angle BAC=90^{\circ}$,$AB = AC = 60\mathrm{cm}$。
$\triangle BMQ$也是等腰直角三角形,则$AQ = MQ = 2y\mathrm{cm}$,$AN = y\mathrm{cm}$。
由$AQ+AN=60$,即$2y + y=60$,解得$y = 20$。
所以$MN = 20\mathrm{cm}$,$MQ = 40\mathrm{cm}$。
根据矩形面积公式$S = MN× MQ$,可得矩形面积$S=20×40 = 800\mathrm{cm}^{2}$。
任务3
解:设$AD = m\mathrm{cm}$,则$DE = m\mathrm{cm}$,$FC = m\mathrm{cm}$,$DF=(60 - m)\mathrm{cm}$。
矩形面积$S=m(60 - m)=-m^{2}+60m$。
对于二次函数$y = ax^{2}+bx + c(a\neq0)$,这里$a=-1$,$b = 60$,$c = 0$,其对称轴为$x=-\frac{b}{2a}=-\frac{60}{2×(-1)} = 30$。
因为$a=-1\lt0$,所以当$m = 30$时,$S$有最大值。
$S_{max}=-30^{2}+60×30=-900 + 1800=900\mathrm{cm}^{2}$。
所以面积最大的矩形纸片的面积是$900\mathrm{cm}^{2}$。
综上,任务1答案为$\boldsymbol{20\mathrm{cm}}$和$\boldsymbol{40\mathrm{cm}}$;任务2答案为$\boldsymbol{800\mathrm{cm}^{2}}$;任务3答案为$\boldsymbol{900\mathrm{cm}^{2}}$。
查看更多完整答案,请扫码查看


