《2025年教与学课程同步讲练九年级数学全一册浙教版》

9. 掷一枚普通的正方体骰子,有下列事件：①掷得的点数是6；②掷得的点数是奇数；③掷得的点数不大于4；④掷得的点数不小于2. 这些事件发生的可能性由大到小排列正确的是 (B)
A.①②③④
B.④③②①
C.③④②①
D.②③①④

答案： B

10. 小芸一家计划去某城市旅行,需要做自由行的攻略,父母给她分配了一项任务：借助网络评价选取该城市的一家餐厅用餐. 小芸根据家人的喜好,选择了甲､乙､丙三家餐厅,对每家餐厅随机选取了1000条网络评价,评价条数统计如下表所示：
 

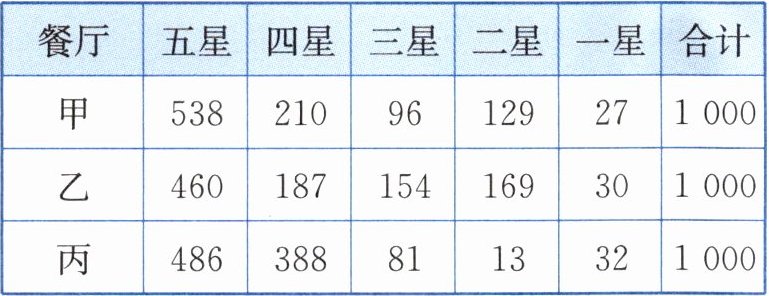
(说明：网上对于餐厅 的综合评价从高到低,依次为五星､四星､三星､二星和一星.)
小芸选择在丙(填“甲”“乙”或“丙”)餐厅用餐,能获得良好用餐体验(即评价不低于四星)的可能性最大.

答案： 丙

11. 不透明 的口袋里有除颜色外其余都相同的红球､白球 和蓝球这三种球,且一共有4个｡甲､乙两名同学玩摸球游戏,规定:无论谁从口袋里随机摸出一个球,摸到红球,算甲赢;摸到白球,算乙赢;摸到蓝球,不分输赢｡每一次摸球,根据球的颜色决定输赢后,将球放回口袋里搅匀后下次再摸球｡请设计下列游戏:
(1)要使甲､乙两人赢 的可能性相等,口袋里应放红球､白球和蓝球各多少个?
(2)要使甲赢 的可能性比乙赢的可能性大,口袋里应放红球､白球和蓝球各多少个?

答案： $(1)$ 使甲、乙两人赢的可能性相等
解：
设红球有$x$个，白球有$y$个，蓝球有$z$个，$x + y+z = 4$（$x,y,z$为非负整数）。
甲赢的概率$P_{甲}=\frac{x}{4}$，乙赢的概率$P_{乙}=\frac{y}{4}$。
要使$P_{甲}=P_{乙}$，即$\frac{x}{4}=\frac{y}{4}$，则$x = y$。
又因为$x + y+z = 4$，当$x = 1$，$y = 1$时，$z=4-(1 + 1)=2$。
所以口袋里应放红球$1$个、白球$1$个、蓝球$2$个。
$(2)$ 使甲赢的可能性比乙赢的可能性大
解：
同样$P_{甲}=\frac{x}{4}$，$P_{乙}=\frac{y}{4}$，要使$P_{甲}＞P_{乙}$，即$\frac{x}{4}＞\frac{y}{4}$，则$x ＞ y$。
又因为$x + y+z = 4$（$x,y,z$为非负整数）。
当$x = 2$，$y = 1$时，$z=4-(2 + 1)=1$。
所以口袋里应放红球$2$个、白球$1$个、蓝球$1$个。
综上，答案依次为：$(1)$ 红球$\boldsymbol{1}$个、白球$\boldsymbol{1}$个、蓝球$\boldsymbol{2}$个；$(2)$ 红球$\boldsymbol{2}$个、白球$\boldsymbol{1}$个、蓝球$\boldsymbol{1}$个 。

12｡如图,一个转盘被平均分成12份,每份上写有不同的数,游戏方法:先猜数后转动转盘,若指针指向的数与所猜 的数一致,则猜数者获胜｡现提供三种猜数方:①猜“是奇数”,或“是偶数”;②猜“是大于10的数”,或“是不大于10的数”;③猜“是3的倍数”,或“不是3的倍数”｡如果你是猜数者,你愿意选择上述哪一种猜数方法?为什么?

答案： 解：选择第③种猜数方法。
理由如下：
- 对于方法①：
奇数有$3$，$17$，$5$，$9$，$21$，$15$共$6$个；偶数有$8$，$10$，$6$，$12$，$14$，$18$共$6$个。
所以猜“是奇数”或“是偶数”获胜的概率$P_1=\frac{6}{12}=\frac{1}{2}$。
对于方法②：
大于$10$的数有$17$，$21$，$14$，$18$，$12$共$5$个；不大于$10$的数有$3$，$8$，$10$，$15$，$6$，$5$，$9$共$7$个。
所以猜“是大于$10$的数”获胜的概率$P_{21}=\frac{5}{12}$，猜“是不大于$10$的数”获胜的概率$P_{22}=\frac{7}{12}$。
对于方法③：
是$3$的倍数的数有$3$，$6$，$9$，$12$，$15$，$18$，$21$共$7$个；不是$3$的倍数的数有$5$，$8$，$10$，$14$，$17$共$5$个。
所以猜“是$3$的倍数”获胜的概率$P_{31}=\frac{7}{12}$，猜“不是$3$的倍数”获胜的概率$P_{32}=\frac{5}{12}$。
因为$\frac{7}{12}＞\frac{1}{2}$，$\frac{7}{12}＞\frac{5}{12}$，所以选择方法③猜“是$3$的倍数”获胜的概率相对较大。