《2025年天府前沿九年级数学上册北师大版》

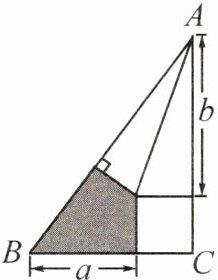
14. (2025·编写)我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理。如图所示,若a= 2,b= 3,现随机向该图形内掷一枚小针,求针尖落在阴影区域内的概率。

答案：
【解】设小正方形的边长为$x$，$\because a = 2$，$b = 3$，$\therefore AB = 2 + 3 = 5$。在$Rt\triangle ABC$中，$AC^{2} + BC^{2} = AB^{2}$，即$(2 + x)^{2} + (x + 3)^{2} = 5^{2}$，解得$x = 1$，$x = -6$（不合题意，舍去），$\therefore S_{\triangle ABC} = \frac{1}{2} \times 3 \times 4 = 6$，$S_{阴影} = \frac{1}{2} \times 2 \times 1 \times 2 = 2$，$\therefore$针尖落在阴影区域内的概率$= \frac{2}{6} =\frac{1}{3}$。

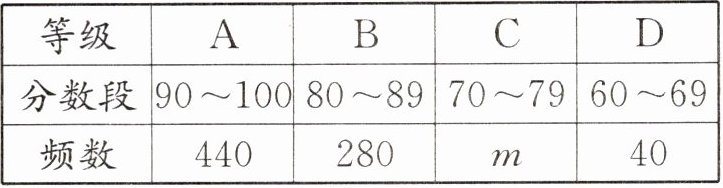
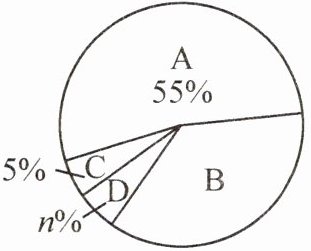
15. (2024·达州)2024年4月21日,达州马拉松暨“跑遍四川”达州站马拉松赛鸣枪开跑,本次赛事以“相约巴人故里,乐跑红色达州”为主题,旨在增强全市民众科学健身意识,推动全民健身活动。本届赛事共设置马拉松、半程马拉松和欢乐跑三个项目。赛后随机抽取了部分参赛选手对本次赛事组织进行满意度评分调查,整理后得到下列不完整的图表：


请根据表中提供的信息,解答下列问题：
(1)此次调查共抽取了____名选手,m= ____,n=
(2)扇形统计图中,B等级所对应的扇形圆心角度数是____度；
(3)赛后若在三个项目的冠军中随机抽取两人访谈,请用列表或画树状图的方法,求出恰好抽到马拉松和欢乐跑冠军的概率。

答案：
【解】
(1) 根据题意，得此次调查共抽取的选手总人数为$440 \div 55\% = 800$，所以$m = 800 \times 5\% = 40$，所以$n\% = \frac{40}{800} = 5\%$，即$n = 5$。故答案为 800；40；5。
(2) 根据题意，得扇形统计图中，B 等级所对应的扇形圆心角度数$= 360^{\circ} \times \frac{280}{800} = 126^{\circ}$。故答案为 126。
(3) 用甲、乙、丙分别表示马拉松、半程马拉松和欢乐跑三个项目。画树状图如下图所示。

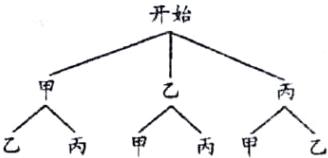
由树状图可知，共有 6 种等可能的结果，其中抽到马拉松和欢乐跑冠军的结果有 2 种，所以恰好抽到马拉松和欢乐跑冠军的概率为$\frac{2}{6} =\frac{1}{3}$。