《2025年天府前沿九年级数学上册北师大版》

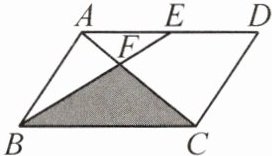
11. (2023·金牛)如图,$E是\square ABCD边AD$的中点,连接$AC$,$BE交于点F$. 现假设可在$\square ABCD$区域内随机取点,则这个点落在阴影部分的概率为______.

答案： $\frac{1}{3}$

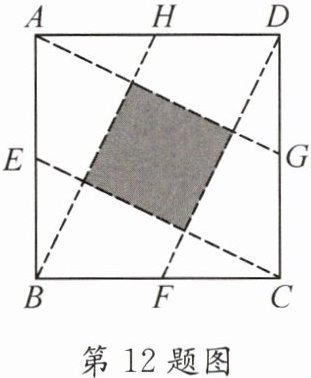
12. (2023·成华)如图,点$E$,$F$,$G$,$H分别是正方形ABCD$四边的中点,$AG$,$BH$,$CE$,$DF$围成图中阴影部分. 随机地往正方形$ABCD$内投掷飞镖,飞镖击中阴影部分的概率是______.

答案： $\frac{1}{5}$

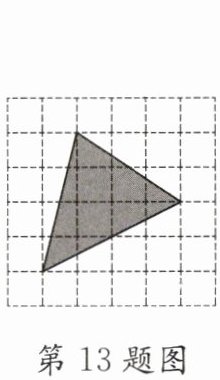
13. (2025·编写)一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格的形状、大小、质地完全相同,当蚂蚁停下来时,停在地板中阴影部分的概率是______.

答案： $\frac{7}{36}$

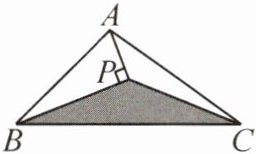
14. (2025·编写)如图,$BP平分\angle ABC$,$AP\perp BP$,垂足为$P$,连接$CP$,若三角形$\triangle ABC内有一点M$,求点$M落在\triangle BPC$内(包括边界)的概率.

答案：
[解]如图，延长$AP$交$BC$于点$E$，
∵$BP$平分$∠ABC$，
∴$∠ABP = ∠EBP$。

∵$AP⊥BP$，
∴$∠APB = ∠EPB = 90^{\circ}$。
在$△ABP$和$△EBP$中，$\begin{cases} ∠ABP = ∠EBP \\ BP = BP \\ ∠APB = ∠EPB \end{cases}$
∴$△ABP≌△EBP(ASA)$，
∴$AP = EP$，
∴$S_{△ABP} = S_{△EBP}$，$S_{△ACP} = S_{△ECP}$，
∴$S_{△PBC} = \frac{1}{2}S_{△ABC}$，
∴点$M$落在$△BPC$内(包括边界)的概率为$\frac{S_{△BPC}}{S_{△ABC}} = \frac{1}{2}$。

15. (2022·广元)为丰富学生课余活动,明德中学组建了$A$体育类、$B$美术类、$C音乐类和D$其他类四类学生活动社团,要求每人必须参加且只参加一类活动. 学校随机抽取八年级(1)班全体学生进行调查,以了解学生参团情况. 根据调查结果绘制了两幅不完整的统计图(如图所示). 请结合统计图中的信息,解决下列问题：
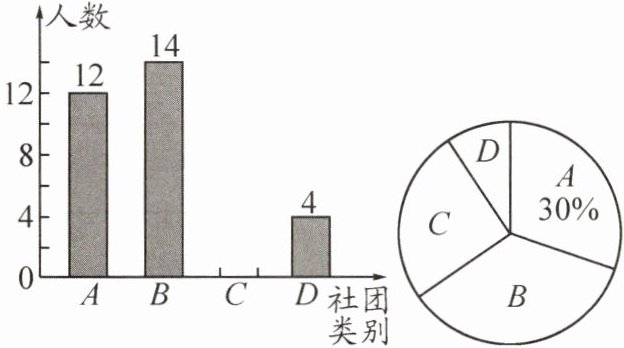
(1)八年级(1)班学生总人数是______人,补全条形统计图,扇形统计图中区域$C$所对应的扇形的圆心角的度数为______；
(2)明德中学共有学生$2500$人,请估算该校参与体育类和美术类社团的学生总人数；
(3)校园艺术节到了,学校将从符合条件的$4$名社团学生(男、女各$2$名)中随机选择两名学生担任开幕式主持人,请用列表或画树状图的方法,求恰好选中$1名男生和1$名女生的概率.

答案：
[解]
(1)$40$ $90^{\circ}$ $C$对应$10$人，补全条形统计图略
(2)$2500×\frac{12 + 14}{40} = 1625$(人)。故估算该校参与体育类和美术类社团的学生有$1625$人。
(3)设男生用$A$表示，女生用$B$表示，画树状图如图：

由上可得，存在$12$种等可能性，其中恰好选中$1$名男生和$1$名女生的可能性有$8$种，故恰好选中$1$名男生和$1$名女生的概率是$\frac{8}{12} = \frac{2}{3}$。