《2025年天府前沿九年级数学上册北师大版》

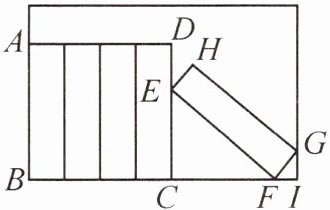
10. (2025·编写)有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点G正好在书架边框上. 每本书的厚度为5cm,高度为20cm,书架宽为40cm,求FI的长度.

答案： [解]由题知，CI=BI−BC=40−20=20(cm)，EF=20cm，FG=5cm，
∵∠EFC+∠CEF=90°，∠EFC+∠GFI=90°，
∴∠CEF=∠GFI；
∵∠ECF=∠FIG=90°，
∴△GIF∽△FCE，
∴$\frac{FI}{CE}=\frac{FG}{EF}$，即$\frac{FI}{CE}=\frac{5}{20}$，
∴CE=4FI.
在Rt△CEF中，由勾股定理，得$CE^{2}+CF^{2}=EF^{2}$，即$(4FI)^{2}+(20−FI)^{2}=20^{2}$，解得$FI=\frac{40}{17}$或FI=0 (舍去)，故FI的长度为$\frac{40}{17}$cm.

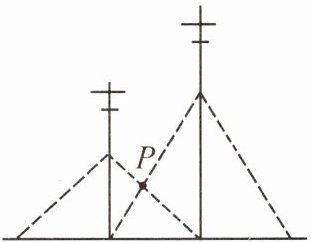
11. (2025·编写)相邻两根电线杆都用钢索在地面上固定,如图,一根电线杆钢索系在离地面4米处,另一根电线杆钢索系在离地面6米处,两根电线杆的钢索都有一根固定在另一根电线杆底部,则中间两根钢索相交处点P离地面______米.

答案： 2.4

12. (2025·编写)公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF//HG,EH⊥HG,AB= 80cm,AD= 24cm,BC= 25cm,EH= 4cm.

(1) 点C到AB的距离为______.
(2) 点A到地面的距离为______.

答案：
(1)24cm　
(2)$\frac{404}{5}$cm

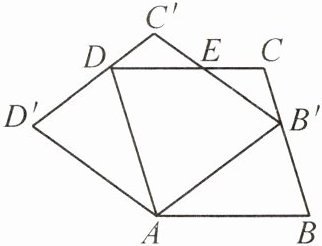
13. (2022·成华)如图,将菱形ABCD绕点A逆时针旋转到菱形AB'C'D'的位置,使点B'落在BC上,B'C'与CD交于点E. 若AB= 5,BB'= 3,则CE的长为______.

答案： $\frac{15}{8}$

14. (2022·自贡)如图,用四根木条钉成矩形框ABCD,把边BC固定在地面上,向右边推动矩形框,矩形的形状会发生改变(四边形具有不稳定性).
(1) 通过观察分析,我们发现图中线段存在等量关系,如线段EB由AB旋转得到,所以EB= AB. 我们还可以得到FC= ______,EF= ______；
(2) 进一步观察,我们还会发现EF//AD,请证明这一结论；
(3) 已知BC= 30cm,DC= 80cm,若BE恰好经过原矩形DC边的中点H,求EF与BC之间的距离.

答案：

(1)CD AD　[解析]
∵把边BC固定在地面上，向右边推动矩形框，矩形的形状会发生改变，
∴矩形ABCD各边的长度没有改变，
∴AB=BE，EF=AD，CF=CD.
(2)[证明]
∵四边形ABCD是矩形，
∴AD//BC，AB=CD，AD=BC；
∵AB=BE，EF=AD，CF=CD，
∴BE=CF，EF=BC，
∴四边形BEFC是平行四边形，
∴EF//BC，
∴EF//AD.
(3)[解]如图，过点E作EG⊥BC交BC的延长线于点G.

∵DC=AB=BE=80cm，H是CD的中点，
∴CH=DH=40cm. 在Rt△BHC中，
$BH=\sqrt{BC^{2}+CH^{2}}=\sqrt{900 + 1600}=50$(cm)，
∵CH⊥BC，EG⊥BC，
∴CH//EG，
∴△BCH∽△BGE，
∴$\frac{BH}{BE}=\frac{CH}{GE}$，
∴$\frac{50}{80}=\frac{40}{GE}$，
∴GE=64，
∴EF与BC之间的距离为64cm.