《2025年天府前沿九年级数学上册北师大版》

1. 等可能事件：设一个试验的所有可能的结果有$n$种,每次试验有且只有其中的______结果出现,而且每种结果出现的可能性______,则称这个试验是______.

答案： 一种　相同　等可能事件

2. 概率的定义：如果一个试验有$n$种等可能的结果,事件$A包含其中的m$种结果,那么事件$A发生的概率为P(A)= $______.

答案： $\frac{m}{n}$

3. 求概率的方法：
(1)利用______或______的方法列举出所有机会均等的结果；
(2)弄清我们关注的是哪个或哪些结果；
(3)求出关注的结果数与所有等可能出现的结果数的比值,即关注事件的概率.

答案：
(1)列表　画树状图　
(2)
(3)

4. 列表法一般应用于两个元素,且结果的可能性较多的题目,当事件涉及三个或三个以上元素时,用树状图列举.

答案： 该表述是正确的。

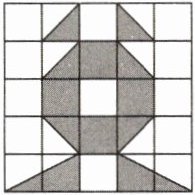
1. (1)(2025·编写)如图,小猫在$5×5$的地板砖上行走,并随机停留在某一块方砖上,则它停留在阴影方砖上的概率是______.

(2)(2025·编写)某路口的交通信号灯每分钟红灯亮$30$秒,绿灯亮$25$秒,黄灯亮$5$秒,当小明到达该路口时,遇到绿灯的概率是______.

答案：
(1)$\frac{9}{25}$　
(2)$\frac{5}{12}$

2. (1)(2025·编写)一只小花猫在如图所示的方砖上走来走去,最终停留在阴影方砖上的概率是______.

(2)(2025·编写)如图所示是一条线段,$AB的长为10$厘米,$MN的长为2$厘米,假设可以随意在这条线段上取一个点,那么这个点取在线段$MN$上的概率为______.

答案：
(1)$\frac{1}{3}$　
(2)$\frac{1}{5}$

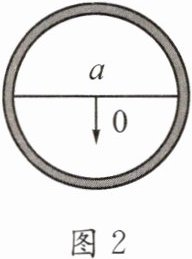
3. (2025·编写)如图所示是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为$0$的概率是______.

答案： $\frac{3}{8}$

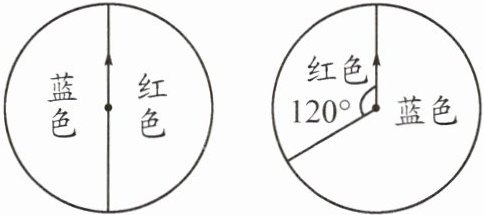
4. (2023·高新)用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是______. (红色和蓝色配成紫色)

答案： $\frac{1}{2}$