《2025年天府前沿九年级数学上册北师大版》

11. (2025·武侯)若 $ x_{1},x_{2} $ 是一元二次方程 $ x^{2}+x - 3 = 0 $ 的两个实数根,则 $ x_{1}^{2}+2x_{1}+x_{2} $ 的值为______.

答案： $ 2 $

12. (1)(2025·编写)已知 $ a,b,c $ 满足 $ 4a^{2}+2b - 4 = 0 $,$ b^{2}-4c + 1 = 0 $,$ c^{2}-12a + 17 = 0 $,则 $ a^{2}+b^{2}+c^{2} $ 等于______.
(2)(2025·编写)若实数 $ x $ 满足方程 $ (x^{2}+2x)(x^{2}+2x - 2)-8 = 0 $,那么 $ x^{2}+2x $ 的值为______.

答案：
(1) $ \frac{29}{4} $
(2) $ 4 $

13. (2025·编写)已知关于 $ x $ 的一元二次方程 $ x^{2}-2x - a = 0 $,有下列结论：① 当 $ a＞-1 $ 时,方程有两个不相等的实根；② 当 $ a＞0 $ 时,方程不可能有两个异号的实根；③ 当 $ a＞-1 $ 时,方程的两个实根不可能都小于 1；④ 当 $ a＞3 $ 时,方程的两个实根一个大于 3,另一个小于 3. 以上 4 个结论中,正确的个数为______.

答案： $ 3 $

14. (2025·武侯)某超市经销一种商品,每千克成本为 30 元,经试销发现,该种商品每天的销售量 $ y $(千克)与销售单价 $ x $(元)满足一次函数关系,其每天销售单价、销售量的四组对应值如下表所示：

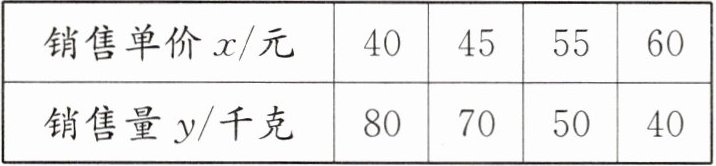
(1) 求 $ y $ 与 $ x $ 之间的函数关系式；
(2) 若商店按销售单价不低于成本价,且不高于 60 元的价格销售,要使销售该商品每天获得的利润为 800 元,则每天的销售单价应为多少元？

答案： 【解】
(1)设 $ y $ 与 $ x $ 之间的函数关系式为 $ y=kx+b $。将 $ (40,80),(45,70) $ 代入 $ y=kx+b $，得 $ \begin{cases}40k+b=80,\\45k+b=70,\end{cases} $ 解得 $ \begin{cases}k=-2,\\b=160.\end{cases} $ $ \therefore y $ 与 $ x $ 之间的函数关系式为 $ y=-2x+160 $。
(2)由题意，得 $ (x-30)(-2x+160)=800 $，解得 $ x_{1}=40,x_{2}=70 $。$ \because $ 商店按销售单价不低于成本价，且不高于 60 元的价格销售，$ \therefore x=40 $，即每天的销售单价应为 40 元。

15. (2023·天府新区)2022 年 11 月 29 日,神舟十五号发射升空,中国首次实现空间站三船三舱构型,以及 6 名航天员同时在轨驻留. 某网店为满足航空航天爱好者的需求,特推出了“中国空间站”模型. 已知该模型平均每天可售出 20 个,每个盈利 40 元. 为了扩大销售,该网店准备适当降价,经过一段时间测算,每个模型每降价 1 元,平均每天可以多售出 2 个.
(1) 若每个模型降价 4 元,平均每天可以售出多少个模型？此时每天获利多少元？
(2) 在每个模型盈利不少于 25 元的前提下,要使“中国空间站”模型每天获利 1200 元,每个模型应降价多少元？

答案： 【解】
(1) $ 20+2\times4=20+8=28 $ (个)，$ (40-4)\times28=36\times28=1008 $ (元)。答：若每个模型降价 4 元，平均每天可以售出 28 个模型，此时每天获利 1008 元。
(2)设每个模型降价 $ x $ 元，则每个模型可盈利 $ (40-x) $ 元，平均每天可售出 $ (20+2x) $ 个。根据题意，得 $ (40-x)(20+2x)=1200 $，整理，得 $ x^{2}-30x+200=0 $，解得 $ x_{1}=10,x_{2}=20 $。又 $ \because $ 每个模型盈利不少于 25 元，$ \therefore x=10 $。答：每个模型应降价 10 元。