《2025年天府前沿九年级数学上册北师大版》

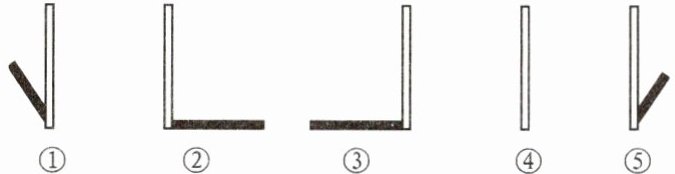
12. (2025·编写)如图是某天不同时刻直立的竹竿及其影长(规定上北下南左西右东),按编号写出竹竿所在时刻的顺序为____。

答案： ③①④⑤②

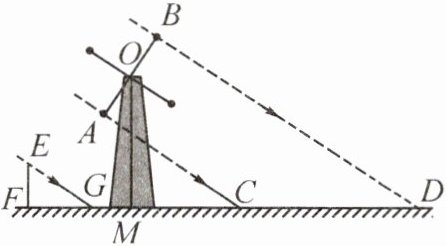
13. (2023·成华)如图是某风车的示意图,其大小相同的四个叶片均匀分布,点M在旋转中心O的正下方。某一时刻,太阳光恰好垂直照射叶片OA,OB,叶片影子为线段CD,测得MC= 8.5米,CD= 13米,此时垂直于地面的标杆EF与它的影子FG的比为2:3(其中点M,C,D,F,G在水平地面上),则OM的高度为____米,叶片OA的长为____米。

答案： $10$　$\sqrt{13}$

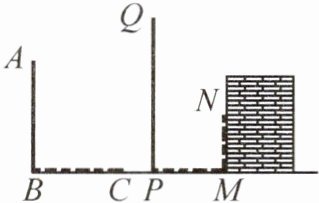
14. (2022·简阳)在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB= 2米,它的影子BC= 1.6米,木杆PQ的影子有一部分落在墙上,PM= 1.2米,MN= 0.8米。求木杆PQ的长度。

答案：
[解]如图，过点$N$作$ND \perp PQ$于点$D$，
可得$\triangle ABC \sim \triangle QDN$，$\therefore \frac{AB}{BC} = \frac{QD}{DN}$。
又$\because AB = 2$米，$BC = 1.6$米，$DN = PM = 1.2$米，$NM = 0.8$米，$\therefore QD = \frac{AB \cdot DN}{BC} = \frac{2 \times 1.2}{1.6} = 1.5$（米），
$\therefore PQ = QD + DP = QD + NM = 1.5 + 0.8 = 2.3$（米）。
故木杆$PQ$的长度为$2.3$米。
　　　　　　

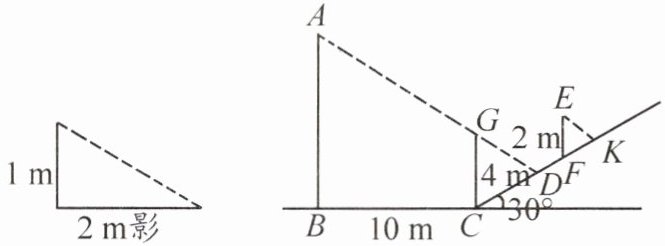
15. (2025·编写)小明想测量电线杆AB的高度,他发现电线杆AB的影子正好落在坡面CD和地面BC上,已知CD和地面成30°角,CD= 4m,BC= 10m,且此时测得1m高的标杆在地面上的影长为2m。
(1) 求电线杆AB的高(结果保留根号)。
(2) 此时,若CG是在坡底下C处的一棵大树,树尖刚好落在光线AD上,则CG= ____m；若在山坡上有一建筑物EF高2m,此时它落在坡面上的影长FK= ____m。(以上结果均保留根号)

答案：

(1)[解]如图，延长$AD$交地面于点$M$，作$DN \perp BC$于点$N$。
$\because CD = 4m$，$\angle DCM = 30^{\circ}$，
$\therefore DN = 4\sin 30^{\circ} = 2(m)$，$CN = 4\cos 30^{\circ} = 2\sqrt{3}(m)$。
$\because 1m$杆的影长为$2m$，$\therefore DN : MN = 1 : 2$，
$\therefore MN = 4m$，
$\therefore AB$的影长$BM = BC + CN + MN = 10 + 2\sqrt{3} + 4 = (14 + 2\sqrt{3})m$，$\therefore$电线杆$AB$的高为$(7 + \sqrt{3})m$。
　　　　　　　
(2)$\sqrt{3} + 2$ $16 - 8\sqrt{3}$ [解析]由题意得$CG // DN$，$\therefore \triangle CGM \sim \triangle NDM$，$\therefore \frac{CG}{DN} = \frac{CM}{MN}$，即$\frac{CG}{2} = \frac{2\sqrt{3} + 4}{4}$，$\therefore CG = (\sqrt{3} + 2)m$。由题意得$CG // EF$，$AD // EK$，$\therefore \angle GCD = \angle EFK$，$\angle GDC = \angle EKF$，$\therefore \triangle CGD \sim \triangle FEK$，$\therefore \frac{FK}{CD} = \frac{EF}{CG}$，即$\frac{FK}{4} = \frac{2}{\sqrt{3} + 2}$，$\therefore FK = (16 - 8\sqrt{3})m$。