《2025年天府前沿九年级数学上册北师大版》

1. 图形中的面积处理方法：平移集中法(如图)。

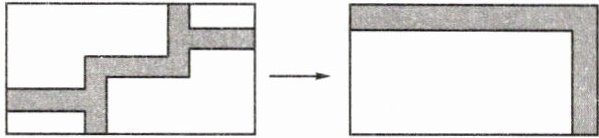
答案： 利用平移集中法可将复杂图形面积计算转化为规则图形面积计算。

2. 图形的周长、面积问题：常借助勾股定理表示线段长度,再根据图形分析建立方程。

答案： 在解决图形的周长、面积问题时，按上述借助勾股定理表示线段长度并根据图形分析建立方程的方法，可有效解决相关问题，具体解题需结合具体题目条件进行操作。

1. (2025·编写)在一幅长为70cm、宽为40cm的矩形风景画的四周镶一条相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是$4800cm^2,$设金色纸边的宽为xcm,那么x满足的方程是______。

答案： $ x^{2}+55x - 500 = 0 $

2. (2025·编写)如图,长方形ABCD的周长是10cm,分别以AB,AD为边向外作正方形ABEF和正方形ADGH.若正方形ABEF和正方形ADGH的面积和为$17cm^2,$则长方形ABCD的面积是______。

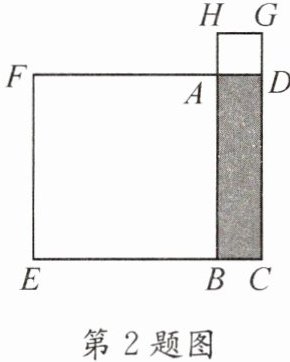
答案： $ 4cm^{2} $

3. (2025·编写)现要在一个长为40m、宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为$864m^2,$那么小道的宽度应是______。

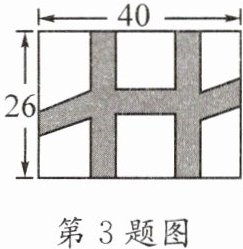
答案： $ 2m $

4. (2022·青羊)如图,李大爷要建一个矩形羊圈.羊圈的一边利用长为12米的住房墙,另外三边是用25米长的彩钢围成的,为了方便进出,在垂直于住房墙的一边留了一扇1米宽的门.当所围矩形与墙垂直的一边长为______米时,羊圈面积为80平方米。

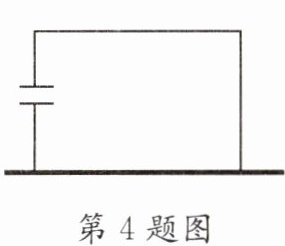
答案： 8

5. (2025·编写)如图是一张长8cm、宽5cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是$18cm^2$的一个无盖长方体纸盒.设剪去的正方形的边长为xcm,那么x满足的方程是()

A. $40 - 4x^{2} = 18$
B. $(8 - 2x)(5 - 2x) = 18$
C. $40 - 2(8x + 5x) = 18$
D. $(8 - 2x)(5 - 2x) = 9$

答案： B

6. (2023·天府新区)《九章算术》是我国古代数学名著,有题译文如下：今有门,不知其高宽；有竿,不知其长短.横放,竿比门宽长出4尺；竖放,竿比门高长出2尺；斜放,竿与门对角线长恰好相等.问门高、宽和对角线的长各是多少？设门对角线的长为x尺,下列方程符合题意的是()
A. $(x + 2)^{2} + (x - 4)^{2} = x^{2}$
B. $(x - 2)^{2} + (x - 4)^{2} = x^{2}$
C. $x^{2} + (x - 2)^{2} = (x - 4)^{2}$
D. $(x - 2)^{2} + x^{2} = (x + 4)^{2}$

答案： B