《2025年天府前沿九年级数学上册北师大版》

6. (2023·新都)若关于 $ x $ 的一元二次方程 $ mx^{2}+3x - 4 = 0 $ 有实数根,则 $ m $ 的值为 ()
A. $ m\geqslant-\frac{9}{16} $ 且 $ m\neq0 $
B. $ m＞-\frac{9}{16} $ 且 $ m\neq0 $
C. $ m\geqslant-\frac{9}{16} $
D. $ m＞-\frac{9}{16} $

答案： A

7. (2025·编写)下列判断正确的是 ()
A. 方程 $ x^{2}= 9x $ 的解是 $ x = 0 $
B. 方程 $ (x + 1)(x - 1)= 1 $ 的解是 $ x= \pm1 $
C. $ 2x^{2}-3x $ 是一元二次方程
D. $ 6x^{2}-1 = 3x $ 的一次项是 $ -3x $

答案： D

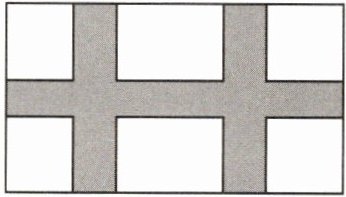
8. (2025·编写)如图,某小区居民休闲娱乐中心是一块长方形(长 60 米,宽 40 米)场地,被 3 条宽度相等的绿化带分为总面积为 1750 平方米的活动场所,设绿化带的宽度为 $ x $ 米,由题意可列方程为 ()

A. $ (60 - x)(40 - x)= 1750 $
B. $ (60 - 2x)(40 - x)= 1750 $
C. $ (60 - 2x)(40 - x)= 2400 $
D. $ (60 - x)(40 - 2x)= 1750 $

答案： B

9. (2025·编写)用适当的方法解下列方程：
(1) $ 2(x + 1)^{2}-\frac{9}{2}= 0 $；
(2) $ (x + 1)(x - 3)= -2 $；
(3) $ x(x + 3)= 5(x + 3) $；
(4) $ (2x + 1)^{2}-3(2x + 1)-28 = 0 $.

答案：
(1)【解】$ 2(x+1)^{2}-\frac{9}{2}=0,2(x+1)^{2}=\frac{9}{2},(x+1)^{2}=\frac{9}{4} $，开平方，得 $ x+1=\pm\frac{3}{2} $，解得 $ x_{1}=\frac{1}{2} $，$ x_{2}=-\frac{5}{2} $。
(2)【解】$ (x+1)(x-3)=-2 $，整理，得 $ x^{2}-2x=1 $，配方，得 $ x^{2}-2x+1=1+1,(x-1)^{2}=2 $，开平方，得 $ x-1=\pm\sqrt{2} $，解得 $ x_{1}=1+\sqrt{2},x_{2}=1-\sqrt{2} $。
(3)【解】$ x(x+3)=5(x+3),x(x+3)-5(x+3)=0,(x+3)(x-5)=0,x+3=0 $ 或 $ x-5=0 $，解得 $ x_{1}=-3,x_{2}=5 $。
(4)【解】$ (2x+1)^{2}-3(2x+1)-28=0 $，设 $ 2x+1=a $，则原方程化为 $ a^{2}-3a-28=0 $，解得 $ a=7 $ 或 $ a=-4 $。当 $ a=7 $ 时，$ 2x+1=7 $，解得 $ x=3 $。当 $ a=-4 $ 时，$ 2x+1=-4 $，解得 $ x=-\frac{5}{2} $。所以原方程的解是 $ x_{1}=3,x_{2}=-\frac{5}{2} $。

10. (1)(2025·编写)某口罩经销商批发了一批口罩,进货单价为每盒 50 元,若按每盒 60 元出售,则每周可销售 80 盒. 现准备提价销售,经市场调研发现：每盒每提价 1 元,每周销量就会减少 2 盒,为保护消费者利益,物价部门规定,销售时利润率不能超过 50%. 设该口罩售价为每盒 $ x(x＞60) $ 元,现在预算销售这种口罩每周要获得 1200 元利润,求每盒口罩的售价.
(2)(2022·郫都)已知关于 $ x $ 的一元二次方程 $ x^{2}-(2m + 1)x + m^{2}-1 = 0 $ 有两个不相等的实数根.
① 求 $ m $ 的取值范围；
② 设 $ x_{1},x_{2} $ 是方程的两根且满足 $ x_{1}^{2}+x_{2}^{2}-9 = 0 $,求 $ m $ 的值.

答案：
(1)【解】由题意，得 $ (x-50)[80-2(x-60)]=1200 $，整理，得 $ x^{2}-150x+5600=0 $。解得 $ x_{1}=70,x_{2}=80 $。当 $ x=70 $ 时，利润率 $ =\frac{70-50}{50}\times100\%=40\%＜50\% $，符合题意；当 $ x=80 $ 时，利润率 $ =\frac{80-50}{50}\times100\%=60\%＞50\% $，不合题意，舍去。所以要获得 1200 元利润，每盒口罩的售价应定为 70 元。
(2)【解】① $ \because $ 方程有两个不相等的实数根，$ \therefore \Delta =b^{2}-4ac=[-(2m+1)]^{2}-4(m^{2}-1)＞0 $，解得 $ m＞-\frac{5}{4} $。②由根与系数的关系可知：$ x_{1}+x_{2}=2m+1,x_{1}\cdot x_{2}=m^{2}-1,\because x_{1}^{2}+x_{2}^{2}-9=0,\therefore (x_{1}+x_{2})^{2}-2x_{1}\cdot x_{2}-9=0,\therefore (2m+1)^{2}-2(m^{2}-1)-9=0 $，整理，得 $ m^{2}+2m-3=0 $，解得 $ m=-3 $ 或 $ m=1 $。$ \because m＞-\frac{5}{4},\therefore m $ 的值为 1。