《2025年天府前沿九年级数学上册北师大版》

8. (2025·编写)已知$\triangle ABC \backsim \triangle DEF$,相似比为$1:2$,且$\triangle DEF的面积为12$,则$\triangle ABC$的面积为()
A. $84$
B. $24$
C. $6$
D. $3$

答案： D

9. (2025·编写)如图,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$\frac{AC}{AB} = \frac{3}{2}$,将$\triangle ABC绕点A顺时针方向旋转角\alpha(0^{\circ} \lt \alpha \lt 90^{\circ})得到\triangle AB'C'$,连接$BB'$,$CC'$,求$\triangle CAC'与\triangle BAB'$的面积之比。

答案： [解]由旋转的性质可知，$∠BAC=∠B'AC'$，
$\therefore ∠BAB'=∠CAC'$.
$\because AB=AB',AC=AC'$,
$\therefore \frac{AB}{AC}=\frac{AB'}{AC'}$,
$\therefore △ACC'\backsim △ABB',\therefore \frac{S_{△ACC'}}{S_{△ABB'}}=(\frac{AC}{AB})^{2}$.
$\because \frac{AC}{AB}=\frac{3}{2},\therefore \frac{S_{△ACC'}}{S_{△ABB'}}=(\frac{AC}{AB})^{2}=\frac{9}{4}$.

10. (2025·编写)如图,$E是矩形ABCD中AD$边的中点,$BE交AC于点F$,$\triangle AEF的面积为2$。求四边形$CDEF$的面积。

答案： [解]$\because$ 四边形$ABCD$为矩形，
$\therefore AD// BC,BC=AD,AB=CD,∠ABC=∠D=90^{\circ }$,
$\therefore S_{△ABC}=S_{△ADC}$.
$\because E$是矩形$ABCD$中$AD$边的中点，
$\therefore BC=AD=2AE$.
$\because AE// BC,\therefore △AEF\backsim △CBF,\therefore \frac{AF}{CF}=\frac{AE}{CB}=\frac{1}{2}$,
$\therefore \frac{S_{△AEF}}{S_{△CBF}}=(\frac{1}{2})^{2}=\frac{1}{4},\therefore S_{△CBF}=4S_{△AEF}=8$,
$\therefore S_{△ABF}=\frac{1}{2}S_{△CBF}=4$,
$\therefore S_{△ABC}=S_{△ADC}=S_{△CBF}+S_{△ABF}=12$,
$\therefore S_{四边形CDEF}=S_{△ADC}-S_{△AEF}=12 - 2 = 10$.

11. (2022·双流)如图,在$\triangle ABC$中,$AD \perp BC$,垂足为$D$,$AD = 5$,$BC = 10$,四边形$EFGH和四边形HGNM$均为正方形,且点$E$,$F$,$G$,$N$,$M都在\triangle ABC$的边上,那么$\triangle AEM与四边形BCME$的面积比为____。

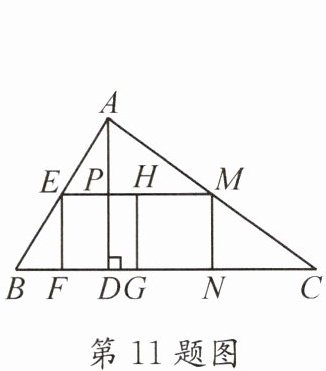
答案： $1:3$

12. (2025·金牛)如图,在$\triangle ABC$中,$D是边AB$上一点,按以下步骤作图：①以点$A$为圆心,以适当长为半径作弧,分别交$AB$,$AC于点M$,$N$；②以点$D$为圆心,以$AM$长为半径作弧,交$DB于点M'$；③以点$M'$为圆心,以$MN$长为半径作弧,在$\angle BAC内部交前面的弧于点N'$；④过点$N'作射线DN'交BC于点E$。若$\triangle BDE与四边形ACED的面积比为1:8$,则$\frac{BE}{CE}$的值为____。

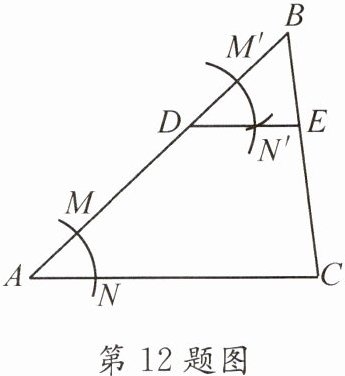
答案： $\frac{1}{2}$

13. (2022·高新)如图,在正方形$ABCD$中,对角线$AC$,$BD相交于点O$,$F是线段OD$上的动点(点$F不与点O$,$D$重合),连接$CF$,过点$F作FG \perp CF分别交AC$,$AB于点H$,$G$,连接$CG交BD于点M$,作$OE // CD交CG于点E$,$EF交AC于点N$。有下列结论：①当$BG = BM$时,$AG = \sqrt{2}BG$；②$\frac{OH}{OM} = \frac{OF}{OC}$；③当$GM = HF$时,$CF^{2} = $ $CN \cdot BC$；④$CN^{2} = BM^{2} + DF^{2}$。其中正确的结论是____。(填序号)

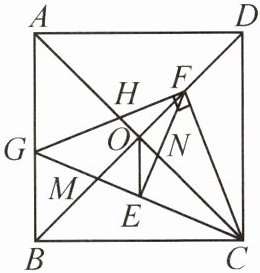
答案： ①③④