《2025年名校课堂九年级数学全一册人教版贵州专版》

11. 下列说法正确的是(D)

A.过弦的中点的直径平分弦所对的两条弧
B.弦的垂直平分线平分它所对的两条弧，但不一定过圆心
C.过弦的中点的直径垂直于弦
D.平分弦所对的两条弧的直径平分弦

答案： D

12. 如图1，筒车是我国古代发明的一种水利灌溉工具. 如图2，筒车盛水桶的运行轨道是以轴心O为圆心的圆，圆心O在水面上方，且⊙O被水面截得弦AB的长为4米，⊙O半径长为3米. 若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是(C)


A.1米
B.2米
C.$(3-\sqrt{5})$米
D.$(3+\sqrt{5})$米

答案： C

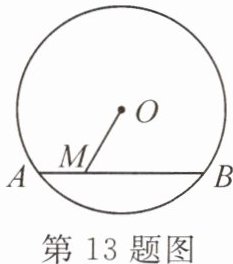
13. 如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM长的最小值为3，最大值为5。

答案： 3 5

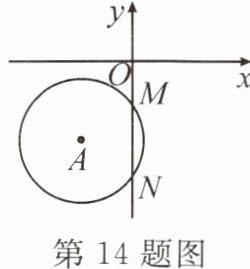
14. 如图，M(0,-3)，N(0,-9)，半径为5的⊙A经过点M，N，则点A的坐标为$(-4,-6)$。

答案： $(-4,-6)$

15. 已知AB，CD是⊙O的两条平行弦，AB=8，CD=6，⊙O的半径为5，则弦AB与CD的距离为1或7。

答案： 1或7

16. 新考向 真实情境 石拱桥是我国古代人民勤劳和智慧的结晶(如图1)，隋代建造的赵州桥距今约有1400年历史，是我国古代石拱桥的代表. 图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧，表示为$\overset{\frown}{AB}$，桥的跨度(弧所对的弦长)AB=26 m. 设$\overset{\frown}{AB}$所在圆的圆心为O，半径OC⊥AB，垂足为D，拱高(弧的中点到弦的距离)CD=5 m，连接OB.
(1)直接判断AD与BD的数量关系.
(2)求这座石拱桥主桥拱的半径(精确到1 m).

答案： 解:
(1)$AD=BD$.
(2)设主桥拱的半径为$r$ m.$\because AB=26$ m,$CD=5$ m,$OC\perp AB$,$\therefore BD=\frac{1}{2}AB=13$ m,$OD=OC-CD=(r-5)$ m.$\because \angle ODB=90°$,$\therefore OD^2+BD^2=OB^2$.$\therefore (r-5)^2+13^2=r^2$,解得$r=19.4\approx19$.
答:这座石拱桥主桥拱的半径约为19 m.

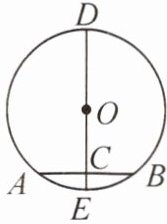
1. 如图，DE是⊙O的直径，弦AB⊥CD，垂足为C. 若AB=6，CE=1，则OC=4，CD=9。

答案： 4 9

2. 如图所示，小区内有个圆形花坛O，点C在弦AB上，AC=11，BC=21，OC=13，则这个花坛的面积为$400\pi$。(结果保留π)

答案： $400\pi$

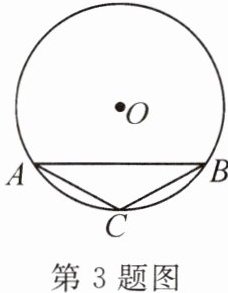
3. 如图，AB是⊙O的弦，C是$\overset{\frown}{AB}$的中点. 若AB=8，⊙O的半径为5，则AC=$2\sqrt{5}$。

答案： $2\sqrt{5}$