《2025年名校课堂九年级数学全一册人教版贵州专版》

7. (2023·黔南期末)某校积极开展全民阅读活动，打造书香校园，在各班建立图书角。据统计，九(10)班第一周参与阅读 128 人次，阅读人次每周递增，到第三周累计参与阅读 608 人次。若设阅读人次的周平均增长率为 $ x $，则可列方程为(D)

A.$ 128(1 + x) = 608 $
B.$ 128(1 + x)^2 = 608 $
C.$ 128(1 + x) + 128(1 + x)^2 = 608 $
D.$ 128 + 128(1 + x) + 128(1 + x)^2 = 608 $

答案： 7.D

8. 新考向 过程性学习(2024·黔南惠水县月考)某商店以每件 70 元的价格购进若干件衬衫，第一个月按单价 100 元销售，售出 200 件，第二个月为增加销售量，且尽可能地让利于顾客，决定降价处理。经市场调查，单价每降低2元，月销售量可增加40件，如何定价，才能使以后每个月的利润为 7820 元？
解：设……。根据题意，得
$ (100 - 70 - x)(200 + \frac{x}{2} × 40) = 7280 $，
……
根据上面所列方程，完成下列任务：
(1) 以上问题中横线处缺少的条件是单价每降低2元，月销售量可增加40件。
(2) 所列方程中未知数 $ x $ 的实际意义是单价降低了x元。
(3) 请写出上面问题的完整解题过程。

答案： 8.解:
(1)单价每降低2元,月销售量可增加40件
(2)单价降低了x元
(3)设单价降低了x元.根据题意,得$(100-70-x)(200+\frac {x}{2}×40)=7280,$整理,得$x^{2}-20x+64=0,$解得$x_{1}=4($舍去$),x_{2}=16.$
∴100-x=100-16=84.
答:定价为每件84元时,才能使以后每个月的利润为7280元.

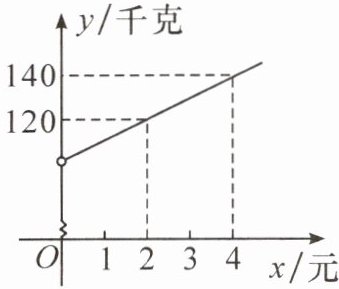
9. 安顺市某商贸公司以每千克 40 元的价格购进一种干果，计划以每千克 60 元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量 $ y $（千克）与每千克降价 $ x $（元）$ (0 ＜ x ＜ 20) $ 之间满足一次函数关系，其图象如图所示。
(1) 求 $ y $ 与 $ x $ 之间的函数关系式。
(2) 若该商贸公司要想获利 2090 元，则这种干果每千克应降价多少元？

答案： 9.解:
(1)设y与x之间的函数关系式为y=kx+b(k≠0),则$\left\{\begin{array}{l} 2k+b=120,\\ 4k+b=140,\end{array}\right. $解得$\left\{\begin{array}{l} k=10,\\ b=100.\end{array}\right. $
∴y与x之间的函数关系式为y=10x+100.
(2)由题意,得(60-40-x)(10x+100)=2090,整理,得x^{2}-10x+9=0.解得x_{1}=1,x_{2}=9.
∵让顾客得到更大的实惠,
∴x=9.
答:若该商贸公司要想获利2090元,则这种干果每千克应降价9元.

10. 某景区 5 月份的游客人数比 4 月份增加了 $ 60\% $，6 月份的游客人数比 5 月份减少了 $ 10\% $。
(1) 设该景区 4 月份的游客人数为 $ a $ 万人，请用含 $ a $ 的代数式填表：

(2) 求该景区 5 月份、6 月份游客人数的月平均增长率。

答案： 10.解:
(1)1.6a 1.44a
(2)该景区5月份、6月份游客人数的月平均增长率为x.根据题意,得$a(1+x)^{2}=1.44a,$解得$x_{1}=0.2=20%,x_{2}=-2.2($不合题意,舍去).
答:该景区5月份、6月份游客人数的月平均增长率为20%.