第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
1. 下列说法中,不正确的是(
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与它自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
D
)A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与它自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
答案:
D
2. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,则下列结论不一定成立的是(

A.CM=DM
B.$\overset{\frown}{CB}=\overset{\frown}{DB}$
C.$\overset{\frown}{AC}=\overset{\frown}{AD}$
D.OM=MB
D
)
A.CM=DM
B.$\overset{\frown}{CB}=\overset{\frown}{DB}$
C.$\overset{\frown}{AC}=\overset{\frown}{AD}$
D.OM=MB
答案:
D
3. (2024·长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为(

A.4
B.$4\sqrt{2}$
C.5
D.$5\sqrt{2}$
B
)
A.4
B.$4\sqrt{2}$
C.5
D.$5\sqrt{2}$
答案:
B
4. 如图,在⊙O中,弦AB垂直平分半径OC,垂足为D. 若⊙O的半径为2,则弦AB的长为

$2\sqrt{3}$
。
答案:
$2\sqrt{3}$
5. (教材九上P83练习T2变式)如图,在⊙O中,AB,AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8 cm,AC=6 cm,那么四边形OEAD的周长为
【拓展设问】 若AB=AC=8 cm,则四边形OEAD的形状为
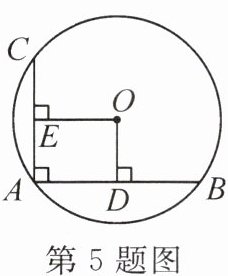
14 cm
。【拓展设问】 若AB=AC=8 cm,则四边形OEAD的形状为
正方形
,⊙O的半径为$4\sqrt{2}$
cm.
答案:
14 cm【拓展设问】正方形 $4\sqrt{2}$
6. (教材九上P90习题T9变式)如图,AB是⊙O的弦,C,D为直线AB上的两点,OC=OD. 求证:AC=BD.
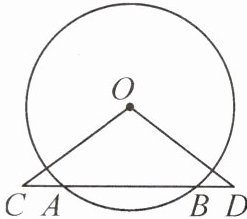

答案:
证明:过点O作$OH\perp AB$于点H,则由垂径定理,得$AH=BH$.$\because OC=OD,OH\perp AB$,$\therefore CH=DH$.$\therefore CH-AH=DH-BH$,即$AC=BD$.
7. (2023·宜昌)如图,OA,OB,OC都是⊙O的半径,AC,OB相交于点D. 若AD=CD=8,OD=6,则BD的长为(
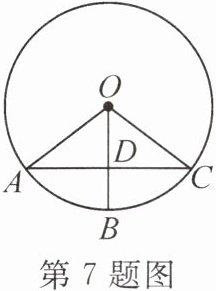
A.5
B.4
C.3
D.2
B
)
A.5
B.4
C.3
D.2
答案:
B
8. 如图所示,⊙O的直径CD=6 cm,AB是⊙O的弦,AM=BM,OM:OC=2:3,则AB的长为

$2\sqrt{5}$
cm.
答案:
$2\sqrt{5}$
9. 新考向 真实情境 如图,这是一种用于液体蒸馏或分馏物质的玻璃容器——蒸馏瓶,其底都是圆球形. 球的半径为5 cm,瓶内液体的最大深度CD=3 cm,则截面圆中弦AB的长为

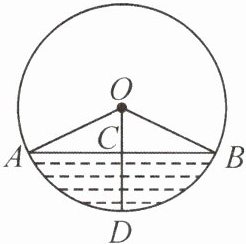
$2\sqrt{21}$
cm.

答案:
$2\sqrt{21}$
10. 新考向 传统文化 如图1,这是中国传统园林建筑中的月亮门,拱门的上部是圆的一段弧. 随着四季更迭,半遮半掩之间,便将丝丝景致幻化成诗情画意. 图2是月亮门的示意图,其中AB=1.8米,C为AB中点,D为月亮门最高点,圆心O在线段CD上,CD=2.7米,月亮门所在圆半径的长为

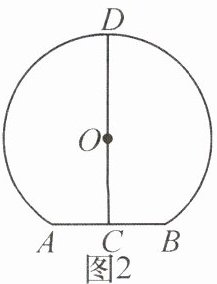
1.5
米.

答案:
1.5
查看更多完整答案,请扫码查看


