《2025年名校课堂九年级数学全一册人教版贵州专版》

8. 新考向 数学文化 (2024·遵义四中期中)我国古代数学著作《增减算法统宗》记载了“圆中方形”问题：“今有圆田一段，中间有个方池。丈量田地待耕犁，恰好三分在记，池面至周有数，每边三步无疑。内方圆径若能知，堪作算中第一。”其大意为：如图，有一块正方形水池，测量出除水池外圆内可耕地的面积恰好是 $81$ 平方步，从水池边到圆周，每边相距 $3$ 步远。设正方形的边长是 $x$ 步，则可列方程为（ ）

A.$\pi(\frac{x}{2} + 6)^2 - x^2 = 81$
B.$\pi(x + 6)^2 - x^2 = 81$
C.$\pi(x + 3)^2 - x^2 = 81$
D.$\pi(\frac{x}{2} + 3)^2 - x^2 = 81$

答案： D

9. 如图所示，某住宅小区内有一矩形地块，想在矩形地块内修筑同样宽的两条“之”字路(图中阴影部分)，余下部分绿化，绿化的面积为 $540\ m^2$，则道路的宽为______m。

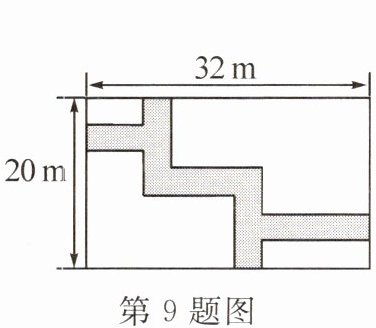
答案： 2

10. (2023·遵义十二中模拟)如图，将边长为 $6\ cm$ 的正方形纸片 $ABCD$ 剪去图中阴影部分的四个全等的直角三角形，再沿图中虚线折起，可以得到一个长方体盒子(点 $A$，$B$，$C$，$D$ 正好重合于上底面一点，且 $AE = BF$)。若得到长方体盒子的表面积为 $11\ cm^2$，则线段 $AE=$________。

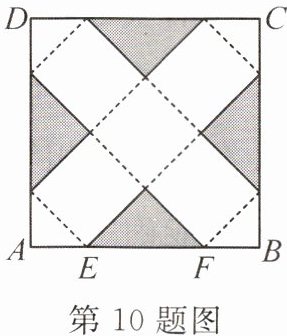
答案： $0.5\ cm$

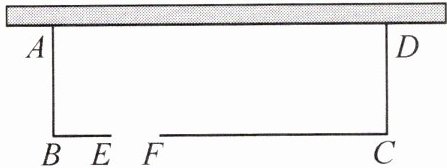
11. (2023·东营改编)如图，老李想用长为 $70\ m$ 的栅栏，再借助房屋的外墙(墙的长度为 $35\ m$)围成一个矩形羊圈 $ABCD$，并在边 $BC$ 上留一个 $2\ m$ 宽的门(建在 $EF$ 处，另用其他材料)。
(1) 当羊圈的长和宽分别为多少米时，能围成一个面积为 $640\ m^2$ 的羊圈？
(2) 羊圈的面积能达到 $650\ m^2$ 吗？如果能，请给出设计方案；如果不能，请说明理由。

答案： 解:
(1)设$AB=x\ m$,则$BC=70-2x+2=(72-2x)\ m$.根据题意,得$x(72-2x)=640$,解得$x_{1}=16$,$x_{2}=20$.当$x=16$时,$72-2x=72-32=40＞35$(不合题意,舍去);当$x=20$时,$72-2x=72-40=32$.
答:当羊圈的长为$32\ m$、宽为$20\ m$时,能围成一个面积为$640\ m^{2}$的羊圈.
(2)不能.理由:根据题意,得$x(72-2x)=650$,化简,得$x^{2}-36x+325=0$.$\because\Delta=(-36)^{2}-4×325=-4＜0$,$\therefore$一元二次方程没有实数根.$\therefore$羊圈的面积不能达到$650\ m^{2}$.

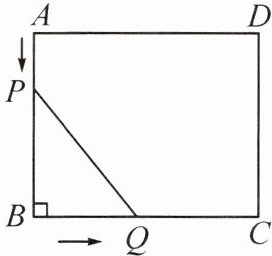
12. 如图，在矩形 $ABCD$ 中，$AB = 5\ cm$，$BC = 6\ cm$，点 $P$ 从点 $A$ 开始，沿边 $AB$ 向终点 $B$ 以 $1\ cm/s$ 的速度移动，与此同时，点 $Q$ 从点 $B$ 开始，沿边 $BC$ 向终点 $C$ 以 $2\ cm/s$ 的速度移动。如果点 $P$，$Q$ 分别从点 $A$，$B$ 同时出发，当点 $Q$ 运动到点 $C$ 时，两点停止运动。设运动时间为 $t\ s$。
(1) 填空：$BQ=$______cm，$PB=$________cm(用含 $t$ 的代数式表示)。
(2) 当 $t$ 为何值时，$PQ$ 的长度等于 $5\ cm$？
(3) 是否存在 $t$ 的值，使得五边形 $APQCD$ 的面积等于 $26\ cm^2$？若存在，请求出此时 $t$ 的值；若不存在，请说明理由。

答案： 解:
(1)$2t$ $(5-t)$
(2)根据题意,得$(5-t)^{2}+(2t)^{2}=5^{2}$,解得$t_{1}=0$,$t_{2}=2$.$\therefore$当$t$的值为$0$或$2$时,$PQ$的长度等于$5\ cm$.
(3)存在,当$t=1$时,五边形$APQCD$的面积等于$26\ cm^{2}$.理由如下:$\because S_{矩形ABCD}=5×6=30(cm^{2})$,$S_{五边形APQCD}=26\ cm^{2}$,$\therefore S_{\triangle PBQ}=30-26=4(cm^{2})$.根据题意,得$\dfrac{1}{2}×(5-t)×2t=4$,解得$t_{1}=4$,$t_{2}=1$.当$t=4$时,$2t=8＞6$,故$t=4$不符合题意,舍去.$\therefore$当$t=1$时,五边形$APQCD$的面积等于$26\ cm^{2}$.