第130页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
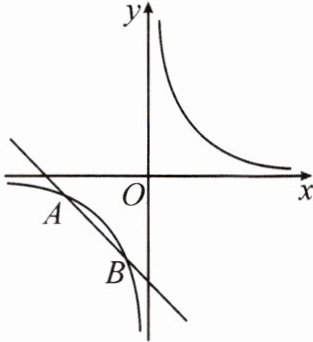
1. (2023·遵义红花岗区模拟)如图,反比例函数 $ y = \frac{8}{x} $ 的图象与一次函数图象 $ y = kx - 5 $($ k $ 为常数,且 $ k \neq 0 $)的图象相交于 $ A $,$ B(-2,m) $ 两点.
(1)求一次函数的解析式.
(2)若将直线 $ AB $ 向上平移 $ n(n > 0) $ 个单位长度后与反比例函数的图象有且只有一个公共点,求 $ n $ 的值.
(1)求一次函数的解析式.
(2)若将直线 $ AB $ 向上平移 $ n(n > 0) $ 个单位长度后与反比例函数的图象有且只有一个公共点,求 $ n $ 的值.

答案:
1.解:
(1)把B(-2,m)代入y=8/x,得m=8/(-2)=-4,
∴B(-2,-4).把B(-2,-4)代入y=kx-5,得-2k-5=-4,解得k=-1/2.
∴一次函数的解析式为y=-1/2x-5.
(2)将直线AB向上平移n(n>0)个单位长度得到的直线的解析式为y=-1/2x-5+n,联立{y=8/x,y=-1/2x-5+n,得8/x=-1/2x-5+n.整理,得1/2x²+(5-n)x+8=0.由题意,得Δ=(5-n)²-4×1/2×8=0.解得n=9或n=1.
∴n的值为1或9.
(1)把B(-2,m)代入y=8/x,得m=8/(-2)=-4,
∴B(-2,-4).把B(-2,-4)代入y=kx-5,得-2k-5=-4,解得k=-1/2.
∴一次函数的解析式为y=-1/2x-5.
(2)将直线AB向上平移n(n>0)个单位长度得到的直线的解析式为y=-1/2x-5+n,联立{y=8/x,y=-1/2x-5+n,得8/x=-1/2x-5+n.整理,得1/2x²+(5-n)x+8=0.由题意,得Δ=(5-n)²-4×1/2×8=0.解得n=9或n=1.
∴n的值为1或9.
解决反比例函数与一次函数交点个数问题,应联立反比例函数与一次函数解析式,构造一元二次方程,根据一元二次方程根的判别式判断交点情况,具体如下:①当 $ \Delta > 0 $ 时,反比例函数与一次函数图象有两个交点;②当 $ \Delta = 0 $ 时,反比例函数与一次函数图象有且只有一个交点;③当 $ \Delta < 0 $ 时,反比例函数与一次函数图象没有交点.
答案:
答题(答题卡内容如下):
设反比例函数为 $y = \frac{k_1}{x}$($k_1 \neq 0$),一次函数为 $y = k_2x + b$($k_2 \neq 0$)。
联立两函数解析式,得:
$\frac{k_1}{x} = k_2x + b$,
整理得:
$k_2x^2 + bx - k_1 = 0$,
根据一元二次方程根的判别式 $\Delta = b^2 - 4ac$,其中 $a = k_2$,$b = b$,$c = -k_1$,得:
$\Delta = b^2 - 4k_2(-k_1) = b^2 + 4k_1k_2$,
① 当 $\Delta > 0$ 时,即 $b^2 + 4k_1k_2 > 0$,反比例函数与一次函数图象有两个交点;
② 当 $\Delta = 0$ 时,即 $b^2 + 4k_1k_2 = 0$,反比例函数与一次函数图象有且只有一个交点;
③ 当 $\Delta < 0$ 时,即 $b^2 + 4k_1k_2 < 0$,反比例函数与一次函数图象没有交点。
设反比例函数为 $y = \frac{k_1}{x}$($k_1 \neq 0$),一次函数为 $y = k_2x + b$($k_2 \neq 0$)。
联立两函数解析式,得:
$\frac{k_1}{x} = k_2x + b$,
整理得:
$k_2x^2 + bx - k_1 = 0$,
根据一元二次方程根的判别式 $\Delta = b^2 - 4ac$,其中 $a = k_2$,$b = b$,$c = -k_1$,得:
$\Delta = b^2 - 4k_2(-k_1) = b^2 + 4k_1k_2$,
① 当 $\Delta > 0$ 时,即 $b^2 + 4k_1k_2 > 0$,反比例函数与一次函数图象有两个交点;
② 当 $\Delta = 0$ 时,即 $b^2 + 4k_1k_2 = 0$,反比例函数与一次函数图象有且只有一个交点;
③ 当 $\Delta < 0$ 时,即 $b^2 + 4k_1k_2 < 0$,反比例函数与一次函数图象没有交点。
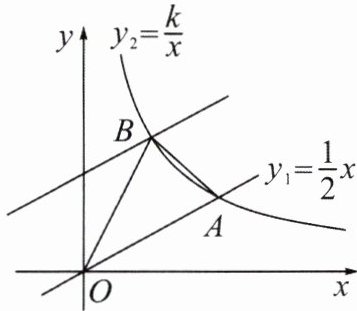
2. (2024·凉山州)如图,正比例函数 $ y_1 = \frac{1}{2}x $ 与反比例函数 $ y_2 = \frac{k}{x}(x > 0) $ 的图象交于点 $ A(m,2) $.
(1)求反比例函数的解析式.
(2)把直线 $ y_1 = \frac{1}{2}x $ 向上平移 3 个单位长度后与 $ y_2 = \frac{k}{x}(x > 0) $ 的图象交于点 $ B $,连接 $ AB $,$ OB $,求 $ \triangle AOB $ 的面积.
(1)求反比例函数的解析式.
(2)把直线 $ y_1 = \frac{1}{2}x $ 向上平移 3 个单位长度后与 $ y_2 = \frac{k}{x}(x > 0) $ 的图象交于点 $ B $,连接 $ AB $,$ OB $,求 $ \triangle AOB $ 的面积.

答案:
2.解:
(1)
∵点A(m,2)在正比例函数y₁=1/2x的图象上,
∴2=1/2m,解得m=4.
∴A(4,2).
∵点A(4,2)在反比例函数y₂=k/x的图象上,
∴k=4×2=8.
∴反比例函数的解析式为y₂=8/x(x>0).
(2)把直线y₁=1/2x向上平移3个单位长度后得到直线y=1/2x+3.设平移后的直线与y轴交于点D,连接AD.由题意,得D(0,3),BD//AO.
∴S△AOB=S△ADO=1/2×3×4=6.
(1)
∵点A(m,2)在正比例函数y₁=1/2x的图象上,
∴2=1/2m,解得m=4.
∴A(4,2).
∵点A(4,2)在反比例函数y₂=k/x的图象上,
∴k=4×2=8.
∴反比例函数的解析式为y₂=8/x(x>0).
(2)把直线y₁=1/2x向上平移3个单位长度后得到直线y=1/2x+3.设平移后的直线与y轴交于点D,连接AD.由题意,得D(0,3),BD//AO.
∴S△AOB=S△ADO=1/2×3×4=6.
反比例函数中求图形面积常用以下方法:
1. 割补法:
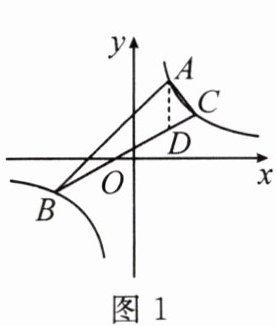
(1)分割法(本例子也叫铅垂法):
如图 1,$ S_{\triangle ABC} = S_{\triangle ABD} + S_{\triangle ACD} = \frac{1}{2}AD \cdot |x_C - x_B| $.
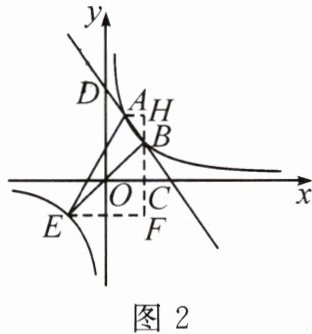
(2)补全法:
如图 2,过点 $ B $ 作 $ HF \perp x $ 轴,过点 $ A $ 作 $ AH \perp HF $ 于点 $ H $,过点 $ E $ 作 $ EF \perp HF $ 于点 $ F $,则 $ S_{\triangle ABE} = S_{梯形AEFH} - S_{\triangle BEF} - S_{\triangle ABH} $.
2. 平行线转移法:
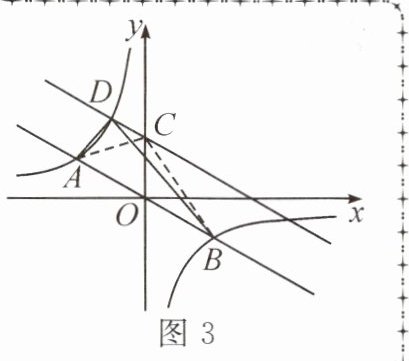
如图 3,若 $ DC // AB $,则 $ S_{\triangle ABD} = S_{\triangle ABC} = S_{\triangle ACO} + S_{\triangle BCO} = \frac{1}{2}OC \cdot |x_A - x_B| $.
1. 割补法:
(1)分割法(本例子也叫铅垂法):
如图 1,$ S_{\triangle ABC} = S_{\triangle ABD} + S_{\triangle ACD} = \frac{1}{2}AD \cdot |x_C - x_B| $.
(2)补全法:
如图 2,过点 $ B $ 作 $ HF \perp x $ 轴,过点 $ A $ 作 $ AH \perp HF $ 于点 $ H $,过点 $ E $ 作 $ EF \perp HF $ 于点 $ F $,则 $ S_{\triangle ABE} = S_{梯形AEFH} - S_{\triangle BEF} - S_{\triangle ABH} $.


2. 平行线转移法:
如图 3,若 $ DC // AB $,则 $ S_{\triangle ABD} = S_{\triangle ABC} = S_{\triangle ACO} + S_{\triangle BCO} = \frac{1}{2}OC \cdot |x_A - x_B| $.

答案:
设反比例函数为$y=\frac{k}{x}(k\neq0)$,以下为不同方法求面积的示例解答(由于原题未给出具体图形坐标等信息,以通用推导为例):
1. 割补法
(1)分割法
假设$A(x_{A},y_{A})$,$B(x_{B},y_{B})$,$C(x_{C},y_{C})$,$D$为$A$到$x$轴垂足相关点(在铅垂法中),$AD$为$A$到$x$轴相关线段长度(具体根据图形),根据$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}=\frac{1}{2}AD\cdot|x_{C}-x_{B}|$,若已知$AD$长度以及$x_{C}$,$x_{B}$的值,直接代入计算即可得到$\triangle ABC$的面积。
(2)补全法
设$A(x_{A},y_{A})$,$B(x_{B},y_{B})$,$E(x_{E},y_{E})$,$H$,$F$为相应垂足点。
先求梯形$AEFH$的面积$S_{梯形AEFH}=\frac{1}{2}(AH + EF)\cdot HF$,其中$AH$为$A$到$HF$的距离,$EF$为$E$到$HF$的距离,$HF$为$B$到$x$轴垂线段长度相关值;$\triangle BEF$的面积$S_{\triangle BEF}=\frac{1}{2}EF\cdot BF$($BF$为$B$,$F$水平或垂直相关长度);$\triangle ABH$的面积$S_{\triangle ABH}=\frac{1}{2}AH\cdot BH$($BH$为$B$,$H$水平或垂直相关长度)。
则$S_{\triangle ABE}=S_{梯形AEFH}-S_{\triangle BEF}-S_{\triangle ABH}$,将相应长度值代入计算。
2. 平行线转移法
设$A(x_{A},y_{A})$,$B(x_{B},y_{B})$,$C$为坐标轴与相关直线交点,$O$为坐标原点,$OC$为坐标轴上相关线段长度。
因为$DC// AB$,所以$S_{\triangle ABD}=S_{\triangle ABC}=S_{\triangle ACO}+S_{\triangle BCO}=\frac{1}{2}OC\cdot|x_{A}-x_{B}|$,已知$OC$长度以及$x_{A}$,$x_{B}$的值,代入计算可得$S_{\triangle ABD}$的面积。
1. 割补法
(1)分割法
假设$A(x_{A},y_{A})$,$B(x_{B},y_{B})$,$C(x_{C},y_{C})$,$D$为$A$到$x$轴垂足相关点(在铅垂法中),$AD$为$A$到$x$轴相关线段长度(具体根据图形),根据$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}=\frac{1}{2}AD\cdot|x_{C}-x_{B}|$,若已知$AD$长度以及$x_{C}$,$x_{B}$的值,直接代入计算即可得到$\triangle ABC$的面积。
(2)补全法
设$A(x_{A},y_{A})$,$B(x_{B},y_{B})$,$E(x_{E},y_{E})$,$H$,$F$为相应垂足点。
先求梯形$AEFH$的面积$S_{梯形AEFH}=\frac{1}{2}(AH + EF)\cdot HF$,其中$AH$为$A$到$HF$的距离,$EF$为$E$到$HF$的距离,$HF$为$B$到$x$轴垂线段长度相关值;$\triangle BEF$的面积$S_{\triangle BEF}=\frac{1}{2}EF\cdot BF$($BF$为$B$,$F$水平或垂直相关长度);$\triangle ABH$的面积$S_{\triangle ABH}=\frac{1}{2}AH\cdot BH$($BH$为$B$,$H$水平或垂直相关长度)。
则$S_{\triangle ABE}=S_{梯形AEFH}-S_{\triangle BEF}-S_{\triangle ABH}$,将相应长度值代入计算。
2. 平行线转移法
设$A(x_{A},y_{A})$,$B(x_{B},y_{B})$,$C$为坐标轴与相关直线交点,$O$为坐标原点,$OC$为坐标轴上相关线段长度。
因为$DC// AB$,所以$S_{\triangle ABD}=S_{\triangle ABC}=S_{\triangle ACO}+S_{\triangle BCO}=\frac{1}{2}OC\cdot|x_{A}-x_{B}|$,已知$OC$长度以及$x_{A}$,$x_{B}$的值,代入计算可得$S_{\triangle ABD}$的面积。
查看更多完整答案,请扫码查看


