《2025年赢在微点数学》

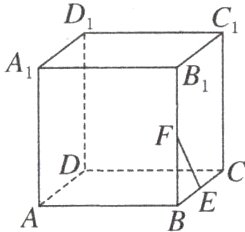
[例2]　(1)如图，在正方体ABCD - A₁B₁C₁D₁中，E，F分别为BC，BB₁的中点，则下列直线中与直线EF相交的是　　　　　　　　　　　　　　　　(　　)

A. 直线AA₁
B. 直线A₁B₁
C. 直线A₁D₁
D. 直线B₁C₁

答案： D 解析 根据异面直线的概念可知直线AA₁，A₁B₁，A₁D₁都和直线EF为异面直线。因为直线B₁C₁和EF在同一平面内，且这两条直线不平行，所以直线B₁C₁和直线EF相交。故选D。

(2)正四面体PABC中，点M是BC的中点，则异面直线PM与AB所成角的余弦值为(　　)
A. $\frac{\sqrt{3}}{3}$
B. $\frac{\sqrt{3}}{6}$
C. $\frac{\sqrt{33}}{6}$
D. $\frac{\sqrt{6}}{3}$

答案：
B 解析 如图，设正四面体的棱长为2，取AC的中点N，连接PN，MN，则PN = PM = √3，MN//AB，且MN = 1，∠PMN即PM与AB所成的角。因为△PMN为等腰三角形，所以取MN的中点O，连接PO，则PO⊥MN，cos∠PMN = $\frac{MO}{PM}=\frac{\frac{1}{2}}{\sqrt{3}}=\frac{\sqrt{3}}{6}$ 。故选B。

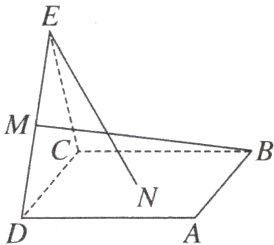
[变式训练]　(1)如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则　　　　　　　　　(　　)

A. BM = EN，且直线BM，EN是相交直线
B. BM≠EN，且直线BM，EN是相交直线
C. BM = EN，且直线BM，EN是异面直线
D. BM≠EN，且直线BM，EN是异面直线

答案：
B 解析 因为N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，连接BD，所以BM⊂平面BDE，EN⊂平面BDE，又BM是△BDE中DE边上的中线，EN是△BDE中BD边上的中线，所以BM，EN是相交直线，设DE = a，则BD = √2a，BE = $\sqrt{\frac{3a^{2}}{4}+\frac{5a^{2}}{4}}=\sqrt{2}a$ ，所以BM = $\frac{\sqrt{7}}{2}a$ ，EN = $\sqrt{\frac{3}{4}a^{2}+\frac{a^{2}}{4}}=a$ ，所以BM≠EN。故选B。

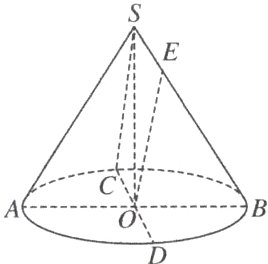
(2)(2024·衡水检测)如图，在圆锥SO中，AB，CD为底面圆的两条直径，AB∩CD = O，且AB⊥CD，SO = OB = 3，SE = $\frac{1}{4}$SB，则异面直线SC与OE所成角的正切值为　　　　　(　　)

A. $\frac{\sqrt{22}}{2}$
B. $\frac{\sqrt{5}}{3}$
C. $\frac{13}{16}$
D. $\frac{\sqrt{11}}{3}$

答案：
D 解析 如图，过点S作SF//OE，交AB于点F，连接CF，则∠CSF(或其补角)为异面直线SC与OE所成的角。因为SE = $\frac{1}{4}SB$ ，所以SE = $\frac{1}{3}BE$ 。又OB = 3，所以OF = $\frac{1}{3}OB = 1$ 。因为SO⊥OC，SO = OC = 3，所以SC = 3√2。因为SO⊥OF，所以SF = $\sqrt{SO^{2}+OF^{2}}=\sqrt{10}$ 。因为OC⊥OF，所以CF = √10。所以在等腰△SCF中，tan∠CSF = $\frac{\sqrt{(\sqrt{10})^{2}-(\frac{3\sqrt{2}}{2})^{2}}}{\frac{3\sqrt{2}}{2}}=\frac{\sqrt{11}}{3}$ 。故选D。

[例3]　(1)已知a，b表示直线，α，β，γ表示平面，则下列推理正确的是　　　　　　　(　　)
A. α∩β = a，b⊂α⇒a//b
B. α∩β = a，a//b⇒b//α且b//β
C. a//β，b//β，a⊂α，b⊂α⇒α//β
D. α//β，α∩γ = a，β∩γ = b⇒a//b

答案： D 解析 选项A中，α∩β = a，b⊂α，则a，b可能平行也可能相交，故A不正确；选项B中，α∩β = a，a//b，则可能b//α且b//β，也可能b在平面α或平面β内，故B不正确；选项C中，a//β，b//β，a⊂α，b⊂α，根据面面平行的判定定理，再加上条件直线a与直线b相交，才能得出α//β，故C不正确；选项D为面面平行性质定理的符号语言。故选D。

(2)(多选题)用一个平面α截正方体，把正方体分为体积相等的两部分，则下列结论正确的是　　　　　　　　　　　　　　　　(　　)
A. 这两部分的表面积一定不相等
B. 截面不会是三角形
C. 截面不会是五边形
D. 截面可以是正六边形

答案：
BCD 解析 如图，一个平面α截正方体，把正方体分为体积相等的两部分，则平面α一定过正方体的中心，所以这两部分的表面积相等，根据对称性，截面不会是三角形、五边形，但可以是正六边形(如图)。故选BCD。