第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
7.如图1,放置两个全等的含有$30^{\circ}$角的直角三角尺ABC与DEF($∠B = ∠E = 30^{\circ}$).若将三角尺ABC向右以每秒1个单位长度的速度移动(点C与点E重合时移动终止),移动过程中始终保持点B,F,C,E在同一条直线上,如图2,AB与DF,DE分别交于点P,M,AC与DE交于点Q,其中$AC = DF = \sqrt{3}$,设三角尺ABC的移动时间为x秒.
(1)在移动过程中,试用含x的代数式表示$△AMQ$的面积.
(2)当x等于多少时,两个三角尺重叠部分的面积有最大值?最大值是多少?

(1)在移动过程中,试用含x的代数式表示$△AMQ$的面积.
(2)当x等于多少时,两个三角尺重叠部分的面积有最大值?最大值是多少?

答案:
解析
(1)
∵在Rt△ABC中,∠B=30°,
∴∠BAC =60°.
∵∠E=30°,
∴∠EQC=∠AQM=60°,
∴△AMQ为等边三角形,如图,过点M作MN⊥AQ,垂足为N;
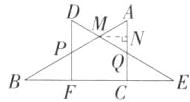
在Rt△ABC中,∠B=30°,AC=$\sqrt{3}$,
∴BC=3,
∴EF=BC=3.根据题意知,CF=x,
∴CE=EF−CF=3−x,
∴CQ=$\frac{\sqrt{3}}{3}$(3−x),
∴AQ=AC−CQ=$\sqrt{3}$−$\frac{\sqrt{3}}{3}$(3−x)=$\frac{\sqrt{3}}{3}$x,
∴AM=AQ=$\frac{\sqrt{3}}{3}$x,
∴MN=$\frac{1}{2}$x,
∴S△AMQ=$\frac{1}{2}$AQ·MN=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x·$\frac{1}{2}$x=$\frac{\sqrt{3}}{12}$x².
(2)由
(1)知BF=CE=3−x,PF=$\frac{\sqrt{3}}{3}$(3−x),设两个三角尺重叠部分的面积为S重叠,
∴S重叠=S△ABC−S△AMQ−S△BPF=$\frac{1}{2}$BC·AC−$\frac{1}{2}$AQ·MN−$\frac{1}{2}$BF·PF=$\frac{1}{2}$×3×$\sqrt{3}$−$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x·$\frac{1}{2}$x−$\frac{1}{2}$(3−x)·$\frac{\sqrt{3}}{3}$(3−x)=−$\frac{\sqrt{3}}{4}$x²+$\sqrt{3}$x=−$\frac{\sqrt{3}}{4}$(x−2)²+$\sqrt{3}$,
∴当x=2时,重叠部分面积有最大值,最大值是$\sqrt{3}$。
解析
(1)
∵在Rt△ABC中,∠B=30°,
∴∠BAC =60°.
∵∠E=30°,
∴∠EQC=∠AQM=60°,
∴△AMQ为等边三角形,如图,过点M作MN⊥AQ,垂足为N;

在Rt△ABC中,∠B=30°,AC=$\sqrt{3}$,
∴BC=3,
∴EF=BC=3.根据题意知,CF=x,
∴CE=EF−CF=3−x,
∴CQ=$\frac{\sqrt{3}}{3}$(3−x),
∴AQ=AC−CQ=$\sqrt{3}$−$\frac{\sqrt{3}}{3}$(3−x)=$\frac{\sqrt{3}}{3}$x,
∴AM=AQ=$\frac{\sqrt{3}}{3}$x,
∴MN=$\frac{1}{2}$x,
∴S△AMQ=$\frac{1}{2}$AQ·MN=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x·$\frac{1}{2}$x=$\frac{\sqrt{3}}{12}$x².
(2)由
(1)知BF=CE=3−x,PF=$\frac{\sqrt{3}}{3}$(3−x),设两个三角尺重叠部分的面积为S重叠,
∴S重叠=S△ABC−S△AMQ−S△BPF=$\frac{1}{2}$BC·AC−$\frac{1}{2}$AQ·MN−$\frac{1}{2}$BF·PF=$\frac{1}{2}$×3×$\sqrt{3}$−$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x·$\frac{1}{2}$x−$\frac{1}{2}$(3−x)·$\frac{\sqrt{3}}{3}$(3−x)=−$\frac{\sqrt{3}}{4}$x²+$\sqrt{3}$x=−$\frac{\sqrt{3}}{4}$(x−2)²+$\sqrt{3}$,
∴当x=2时,重叠部分面积有最大值,最大值是$\sqrt{3}$。
8.新应用意识 [2024江苏无锡江阴南菁高级中学实验学校月考]无锡阳山是闻名遐迩的“中国水蜜桃之乡”,每年6月至8月,总会吸引大批游客前来品尝,当地某商家为回馈顾客,两周内将标价为20元/千克的水蜜桃经过两次降价后变为16.2元/千克,并且两次降价的百分率相同.
(1)求每次降价的百分率.
(2)①从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示:
|时间x/天|1≤x<9|9≤x<15|
|售价/(元/千克)|第1次降价后的价格|第2次降价后的价格|
|销量/千克|105-3x|120-x|
|储存和损耗费用/元|40+3x|$3x^2-68x+300$|
已知该种水果的进价为8.2元/千克,设销售该水果第x天的利润为y元,求y与x(1≤x<15)之间的函数解析式,并求出第几天时销售利润最大.
②在①的条件下,这14天中有多少天的销售利润不低于930元?请直接写出结果.
(1)求每次降价的百分率.
(2)①从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示:
|时间x/天|1≤x<9|9≤x<15|
|售价/(元/千克)|第1次降价后的价格|第2次降价后的价格|
|销量/千克|105-3x|120-x|
|储存和损耗费用/元|40+3x|$3x^2-68x+300$|
已知该种水果的进价为8.2元/千克,设销售该水果第x天的利润为y元,求y与x(1≤x<15)之间的函数解析式,并求出第几天时销售利润最大.
②在①的条件下,这14天中有多少天的销售利润不低于930元?请直接写出结果.
答案:
解析
(1)设每次降价的百分率为x,根据题意得20(1−x)²=16.2,解得x₁=0.1=10%,x₂=1.9(舍去).
∴每次降价的百分率为10%.
(2)①结合
(1)得第一次降价后的价格为20×(1−10%)=18元/千克,当1≤x<9时,y=(18−8.2)(105−3x)−(40+3x)=−32.4x+989,
∵k=−32.4<0,
∴y随着x 的增大而减小,
∴当x=1时,y有最大值,为−32.4×1+989=956.6;当9≤x<15时,y=(16.2−8.2)×(120−x)−(3x²−68x+300)=−3x²+60x+660=−3(x−10)²+960,
∵a=−3<0,
∴当x=10时,y有最大值,为960.
∵956.6<960,
∴第10天时销售利润最大.综上可得y=$\begin{cases}-32.4x + 989(1\leq x\lt9)\\-3x^2 + 60x + 660(9\leq x\lt15)\end{cases}$,第10天时销售利润最大.
②当1≤x<9时,令−32.4x+989≥930,解得x≤$\frac{295}{162}$,
∴第1天的销售利润不低于930元;当9≤x<15时,令−3x²+60x+660≥930,解得10−$\sqrt{10}$≤x≤10+$\sqrt{10}$,
∴9≤x≤10+$\sqrt{10}$≈13,
∴第9~13天的销售利润不低于930元,13−9+1=5(天).故共有1+5=6天的销售利润不低于930元。
(1)设每次降价的百分率为x,根据题意得20(1−x)²=16.2,解得x₁=0.1=10%,x₂=1.9(舍去).
∴每次降价的百分率为10%.
(2)①结合
(1)得第一次降价后的价格为20×(1−10%)=18元/千克,当1≤x<9时,y=(18−8.2)(105−3x)−(40+3x)=−32.4x+989,
∵k=−32.4<0,
∴y随着x 的增大而减小,
∴当x=1时,y有最大值,为−32.4×1+989=956.6;当9≤x<15时,y=(16.2−8.2)×(120−x)−(3x²−68x+300)=−3x²+60x+660=−3(x−10)²+960,
∵a=−3<0,
∴当x=10时,y有最大值,为960.
∵956.6<960,
∴第10天时销售利润最大.综上可得y=$\begin{cases}-32.4x + 989(1\leq x\lt9)\\-3x^2 + 60x + 660(9\leq x\lt15)\end{cases}$,第10天时销售利润最大.
②当1≤x<9时,令−32.4x+989≥930,解得x≤$\frac{295}{162}$,
∴第1天的销售利润不低于930元;当9≤x<15时,令−3x²+60x+660≥930,解得10−$\sqrt{10}$≤x≤10+$\sqrt{10}$,
∴9≤x≤10+$\sqrt{10}$≈13,
∴第9~13天的销售利润不低于930元,13−9+1=5(天).故共有1+5=6天的销售利润不低于930元。
查看更多完整答案,请扫码查看


