《2025年5年中考3年模拟九年级数学全一册苏科版》

1. 「2025山西晋城陵川期中」如图,书写汉语拼音的“四线三格”是由等长度的四条平行横线组成的,且相邻两条横线之间的距离相等.小明在“四线三格”里画了一个直角三角形ABC,$∠ABC = 90^{\circ}$.若线段$AB = 1$,$BC = 2$,则“四线三格”相邻两条横线之间的距离是( )


A.$\frac{1}{2}$
B.$\frac{2}{5}$
C.$\frac{3}{5}$
D.$\frac{1}{5}$

答案：
B　过点A作AE⊥点B所在横线于点E,过点C作CD⊥点B所在横线于点D,如图所示，

设“四线三格”相邻两条横线之间的距离是x,则AE=2x,CD=3x,
∵∠ABC=90°,
∴∠ABE+∠CBD=90°,
∵∠ABE+∠BAE=90°,
∴∠BAE=∠CBD,
∴△ABE∽△BCD,
∴$\frac{AE}{BD}=\frac{AB}{BC}=\frac{1}{2}$,
∴$\frac{2x}{BD}=\frac{1}{2}$,
∴BD=4x,在Rt△BCD中,根据勾股定理,得$BD^2+CD^2=BC^2$,
∴$16x^2+9x^2=4$,
∴$x=\frac{2}{5}$,
∴“四线三格”相邻两条横线之间的距离是$\frac{2}{5}$.故选B.

2. 如图,在四边形ABCD中,$∠ADC = 90^{\circ}$,$AD = 1$,$CD = 2$,$BC = 2\sqrt{5}$,$AB = 5$.求BD的长.

答案：
解析　如图,连接AC,作BH⊥DC交DC的延长线于H.
在Rt△ADC中,
∵∠ADC=90°,AD=1,CD=2,
∴$AC=\sqrt{1^2+2^2}=\sqrt{5}$,

∵$AC^2+BC^2=5+20=25$,$AB^2=5^2=25$,
∴$AC^2+BC^2=AB^2$,
∴∠ACB=90°,
∴∠ADC=∠ACB=∠CHB=90°,易证△ACD∽△CBH,
∴$\frac{AD}{CH}=\frac{DC}{BH}=\frac{AC}{BC}$,
∴$\frac{1}{CH}=\frac{2}{BH}=\frac{\sqrt{5}}{2\sqrt{5}}$,
∴CH=2,BH=4,
∴DH=CD+CH=4,在Rt△BDH中,$BD=\sqrt{4^2+4^2}=4\sqrt{2}$.

3. 「2025浙江宁波海曙校级月考」已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1) 如图①,若四边形ABCD是矩形,且$∠AED = ∠BCF$,求证：$\frac{DE}{CF} = \frac{AD}{DC}$.
(2) 如图②,若将(1)中的矩形ABCD改为一般的平行四边形,其余条件不变,求证：$\frac{DE}{CF} = \frac{AD}{DC}$.
(3) 如图③,若$BA = BC = 6$,$DA = DC = 8$,$∠BAD = 90^{\circ}$,$DE ⊥ CF$,请直接写出$\frac{DE}{CF}$的值.

答案：
解析　
(1)证明:
∵四边形ABCD是矩形,
∴∠A=∠FDC=90°,AD//BC,
∴∠BCF=∠CFD,
∵∠AED=∠BCF,
∴∠AED=∠CFD,
∵∠A=∠CDF,
∴△AED∽△DFC,
∴$\frac{DE}{CF}=\frac{AD}{DC}$.
(2)证明:
∵四边形ABCD是平行四边形,
∴AB//CD,AD//BC,
∴∠BCF=∠CFD,
∵∠AED=∠BCF,
∴∠CFD=∠AED,
∵∠GDF=∠ADE,
∴△DFG∽△DEA,
∴$\frac{DF}{DG}=\frac{DE}{AD}$,
∵AB//CD,
∴∠AED=∠CDG,
∵∠CFD=∠AED,
∴∠CFD=∠CDG,
∵∠DCF=∠GCD,
∴△CGD∽△CDF,
∴$\frac{DF}{DG}=\frac{CF}{CD}$,
∴$\frac{DE}{AD}=\frac{CF}{CD}$,
∴$\frac{DE}{CF}=\frac{AD}{CD}$.
(3)$\frac{25}{24}$.
详解:如图,过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,

∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,在△BAD和△BCD中,$\begin{cases}AD=CD,\\AB=BC,\\BD=BD,\end{cases}$
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴$\frac{CM}{CN}=\frac{BC}{CD}$,
∴$\frac{CM}{x}=\frac{3}{4}$,
∴$CM=\frac{3}{4}x$,在Rt△CMB中,$CM=\frac{3}{4}x$,BM=AM - AB=x - 6,由勾股定理得$BM^2+CM^2=BC^2$,
∴$(x - 6)^2+(\frac{3}{4}x)^2=6^2$,解得$x_1=0$(舍去),$x_2=\frac{192}{25}$,
∴$CN=\frac{192}{25}$,
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴$\frac{DE}{CF}=\frac{AD}{CN}=\frac{25}{24}$.

4. 「2025江苏南京江宁东山外国语学校月考」如图,在$△ABC$中,AD是BC边上中线,F是线段AD上一点,且$AF:FD = 2:3$,连接CF并延长交AB于E,则$AE:EB$等于( )

A.$1:2$
B.$2:3$
C.$1:3$
D.$3:5$

答案：
C　如图,过点D作DH//CE,交AB于H,
∵AD是BC边上中线,
∴BD=DC,

∴BH=HE,
∵DH//CE,
∴AE : EH=AF : FD=2 : 3,
∴AE : EB=1 : 3,故选C.

5. 「2024浙江一模」如图,点D,E,F分别在$△ABC$的边上,$\frac{AD}{BD} = \frac{1}{3}$,$DE // BC$,$EF // AB$,点M是DF的中点,连接CM并延长交AB于点N,则$\frac{MN}{CM}$的值是( )

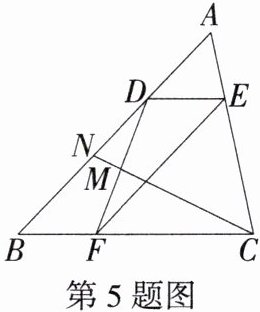
A.$\frac{1}{5}$
B.$\frac{2}{9}$
C.$\frac{1}{6}$
D.$\frac{1}{7}$

答案：
D　如图,过点F作FG//CN交AB于点G,
∵点M是DF的中点,
∴N是DG的中点,

∴MN是△DGF的中位线,
∴GF=2MN,
∵GF//CN,EF//AB,
∴四边形GFHN是平行四边形,
∴NH=GF=2MN,
∴MH=MN,设MH=MN=a,则GF=2a,
∵DE//BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AD}{AB}=\frac{1}{4}$,
∴BC=4DE,
∵EF//AB,DE//BC,
∴四边形DEFB是平行四边形,
∴DE=BF,
∵FG//CN,
∴△BFG∽△BCN,
∴$\frac{BF}{BC}=\frac{GF}{CN}$,
∵$\frac{BF}{BC}=\frac{DE}{BC}=\frac{1}{4}$,
∴$\frac{GF}{CN}=\frac{1}{4}$,
∴CN=4GF=8a,
∴CH=CN - NH=8a - 2a=6a,
∴CM=CH+MH=6a+a=7a,
∴$\frac{MN}{CM}=\frac{a}{7a}=\frac{1}{7}$,故选D.