《2025年5年中考3年模拟九年级数学全一册苏科版》

10. 「2024江苏南京外国语学校淮安分校月考,☆」若数据a,b,c的平均数是2,数据d,e的平均数是3,则数据a,b,c,4,d,e的平均数是$\frac{8}{3}$。

答案： 答案 $\frac{8}{3}$ 解析
∵数据a,b,c的平均数是2,数据d,e的平均数是3,
∴$a+b+c=2×3=6$,$d+e=3×2=6$,
∴a,b,c,4,d,e的平均数是$(a+b+c+4+d+e)÷6=(6+4+6)÷6=\frac{8}{3}$.

11. 「2024广东广州黄埔月考,☆」某单位招录考试计算成绩标准是综合成绩= 笔试成绩×60%+面试成绩×40%(笔试成绩与面试成绩均为整数),已知小明的笔试成绩是82分,小芳的笔试成绩是85分,若小明的综合成绩要超过小芳,则小明的面试成绩至少比小芳多5分。

答案： 答案 5 解析 设小明的面试成绩为x分,小芳的面试成绩为y分,则$82×60\%+40\%x＞85×60\%+40\%y$,
∴$0.4x-0.4y＞(85-82)×0.6$,
∴$x-y＞4.5$,故小明的面试成绩至少比小芳多5分.

12. 「2023江苏南通启东长江中学期末,☆」对于三个数a,b,c,用$M\{a,b,c\}$表示这三个数的平均数,用$min\{a,b,c\}$表示这三个数中最小的数。例如,$M\{-1,2,3\}= \frac{-1+2+3}{3}= \frac{4}{3}$,$min\{-1,2,3\}= -1$,如果$M\{3,2x+1,x-1\}= min\{3,-x+7,2x+5\}$,那么x= 2或-4。

答案： 答案 2或-4 解析 $M|3,2x+1,x-1|=min|3,-x+7,2x+5|$,①若$\frac{1}{3}(3+2x+1+x-1)=3$,则$x=2$(符合题意);②若$\frac{1}{3}(3+2x+1+x-1)=-x+7$,则$x=3$,此时$-x+7$不是三个数中最小的数,不符合题意;③若$\frac{1}{3}(3+2x+1+x-1)=2x+5$,则$x=-4$(符合题意).综上,x的值为2或-4.

13. 「2025江苏南京建邺期中,☆」为了解某校八年级学生暑假期间每天的睡眠时长(单位：h),随机调查了该校八年级a名学生,得到如下统计图。

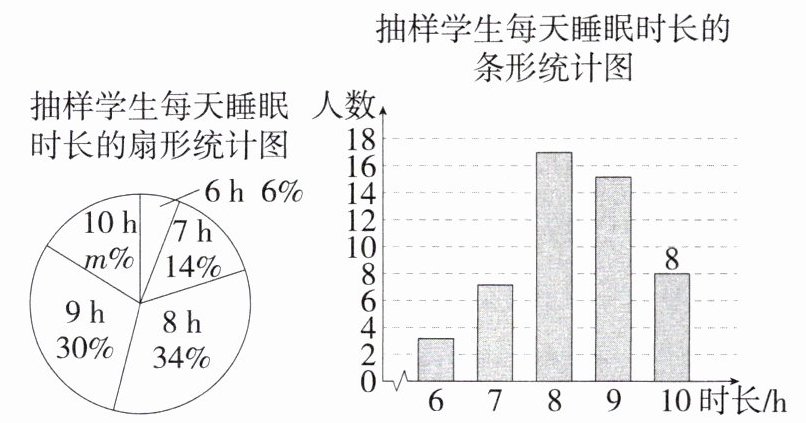
(1)$m$= 16,$a$= 50。
(2)求抽样学生每天睡眠时长的平均数。
$\frac{6×3+7×7+17×8+15×9+8×10}{50}=8.36$(h).答:抽样学生每天睡眠时长的平均数为8.36 h.
(3)根据样本数据,若该校八年级共有学生400人,估计该校八年级学生暑假期间每天睡眠时长不足8h的人数。
$400×(6\%+14\%)=400×20\%=80$.答:该校八年级学生暑假期间每天睡眠时长不足8 h的人数约为80.

答案： 解析
(1)$a=3+7+17+15+8=50$,$m\%=\frac{8}{50}×100\%=16\%$,故$m=16$.故答案为16;50.
(2)$\frac{6×3+7×7+17×8+15×9+8×10}{50}=8.36$(h).答:抽样学生每天睡眠时长的平均数为8.36 h.
(3)$400×(6\%+14\%)=400×20\%=80$.答:该校八年级学生暑假期间每天睡眠时长不足8 h的人数约为80.

14. 「2023江苏南通海门二模」气象学上,将某一天及其前后各两天的“日平均气温”的平均数称为“5天滑动平均气温”,由这两种数值可以确定“入夏日”。例如,2021年某地区从5月27日起,“5天滑动平均气温”首次连续5天大于或等于22℃,其中5月26日的“日平均气温”是5月27日及其前后各两天中第一个大于或等于22℃的,则5月26日便是2021年该地区的“入夏日”。
已知该地区2022年“入夏日”为图中的某一天,请根据统计图回答问题：

(1)求2022年5月27日的“5天滑动平均气温”。
(2)直接写出2022年的“入夏日”。
(3)某人说：“该地区2022年的春天比2021年长。”你认为这样的说法正确吗？为什么？(该地区2021年、2022年的入春日分别是3月23日和3月8日)

答案： 解析
(1)$\frac{1}{5}×(22+21+23+21+23)=22$(℃).答:2022年5月27日的“5天滑动平均气温”为22℃.
(2)该地区2022年的“入夏日”为5月25日.
(3)正确.理由:因为该地区2022年的入夏时间虽然比2021年早了2天,但是2022年的入春时间比2021年早了15天,所以该地区2022年的春天应该比2021年还长.