《2025年5年中考3年模拟九年级数学全一册苏科版》

8.「2025江苏无锡外国语学校期中」如图,平面直角坐标系中,$A(2,0),B(1,2),C(-1,1)$,以A为位似中心,把$△ABC$在点A左侧按相似比$1:3$放大,放大后的图形记作$△AB_{1}C_{1}$,则$C_{1}$的坐标为____.

答案：
答案 $(-7,3)$解析 过C作$CM⊥x$轴于点M,过$C_{1}$作$C_{1}N⊥x$轴于点N,如图,

∵$A(2,0),C(-1,1)$,
∴$OA=2,OM=1,CM=1$,
∵以A为位似中心,把$△ABC$在点A左侧按相似比1:3放大,放大后的图形记作$△AB_{1}C_{1}$,
∴$\frac{AC}{AC_{1}}=\frac{1}{3}$,
∵$CM//C_{1}N$,
∴$△ACM∽△AC_{1}N$,
∴$\frac{AM}{AN}=\frac{CM}{C_{1}N}=\frac{AC}{AC_{1}}=\frac{1}{3}$,
∴$C_{1}N=3CM=3,AN=3AM=3×3=9$,
∴$ON=AN - OA=9 - 2=7$,
∴点$C_{1}$的坐标为$(-7,3)$.

9.「2024江苏无锡中考」如图,在$△ABC$中,$AC= 2,AB= 3$,直线$CM// AB$,E是BC上的动点(端点除外),射线AE交CM于点D,在射线AE上取一点P,使得$AP= 2ED$,作$PQ// AB$,交射线AC于点Q.设$AQ= x,PQ= y$.当$x= y$时,$CD= $2;在点E运动的过程中,y关于x的函数表达式为$y=\frac{3x^{2}}{8 - 2x}$.

答案： 答案 $2;y=\frac{3x^{2}}{8 - 2x}$解析
∵$CM//AB,PQ//AB$,
∴$CD//PQ$,
∴$△APQ∽△ADC$,
∴$\frac{AQ}{AC}=\frac{PQ}{CD}$,即$\frac{x}{2}=\frac{y}{CD}$,整理得$CD=\frac{2y}{x}$,当$x=y$时,$CD=2$.
设$DE=t$,
∵$AP=2ED$,
∴$AP=2t$,
∵$CM//AB$,
∴$△CDE∽△BAE$,
∴$\frac{CD}{AB}=\frac{DE}{AE}$,即$\frac{\frac{2y}{x}}{3}=\frac{t}{AE}$,整理得$AE=\frac{3xt}{2y}$,
∴$AD=AE + DE=\frac{3xt}{2y}+t=\frac{t(3x + 2y)}{2y}$,
∵$△APQ∽△ADC$,
∴$\frac{AQ}{AC}=\frac{AP}{AD}$,即$\frac{x}{2}=\frac{2t}{\frac{t(3x + 2y)}{2y}}$,整理得$y=\frac{3x^{2}}{8 - 2x}$.

10.「2024江苏苏州高新实验中学期中」(12分)图①、图②、图③均是$6×6$的正方形网格,每个小正方形的顶点称为格点,点A、B、C、D均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写画法,要求保留必要的作图痕迹.
(1)在图①中以线段AD为边画一个三角形,使它与$△ABC$相似.
(2)在图②中画一个三角形,使它与$△ABC$相似(不全等).
(3)在图③中的线段AB上画一个点P,使$\frac {AP}{PB}= \frac {2}{3}$.

答案：

(1)如图①,$△ADE$即为所求.
(2)如图②,$△FGH$即为所求.
(3)如图③,点P即为所求.

11.「2025江苏泰州靖江期末」(10分)如图,在等边$△ABC$中,点D是边BC上一个动点(不与A,B重合),点E在AC上,且$∠ADE= 60^{\circ }.$
(1)求证:$△ABD\backsim △DCE.$
(2)若等边$△ABC$的边长为3,求AE的最小值.

答案：
(1)证明:
∵$△ABC$是等边三角形,
∴$∠B=∠C=60°$,
∵$∠ADC=∠ADE + ∠CDE,∠ADC=∠B + ∠BAD,∠ADE=∠B=60°$,
∴$∠CDE=∠BAD$,
∴$△ABD∽△DCE$.
(2)设$BD=x$,则$CD=3 - x$,
∵$△ABD∽△DCE$,
∴$\frac{BD}{CE}=\frac{AB}{CD}$,
∴$\frac{x}{CE}=\frac{3}{3 - x}$,
∴$CE=-\frac{1}{3}x^{2}+x$,易知当$x=-\frac{1}{2×(-\frac{1}{3})}=\frac{3}{2}$时,CE取得最大值$\frac{3}{4}$,此时AE取得最小值,为$\frac{9}{4}$.

12.「2025江苏盐城东鸣湖实验学校期末」(10分)如图,在阳光下,某一时刻,旗杆AB的影子一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB在地面上的影长BC为16 m,在墙面上的影长CD为3 m.同一时刻,直立于地面长1 m的标杆的影长为0.8 m,求旗杆AB的高度.

答案：
如图,过点D作$DE⊥AB$于E,
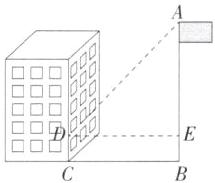
∵$DC⊥BC,AB⊥BC$,
∴四边形BCDE为矩形,
∴$DE=BC=16m,BE=DC=3m$,
∵同一时刻,物高与影长成比例,
∴$\frac{1}{0.8}=\frac{AE}{16}$,
∴$AE=20m$,
∴$AB=20 + 3=23(m)$.答:旗杆的高度为23m.

13.「2024江苏苏州相城蠡口中学月考」(14分)如图,$△ABC是\odot O$的内接三角形,AB是$\odot O$的直径,$AC= 3,BC= 4$,CD平分$∠ACB$,交AB于点F,连接BD,作$BE⊥CD$,垂足为E.
(1)求证:$△ACF\backsim △DCB.$
(2)求证:$AC+BC= \sqrt {2}CD.$
(3)求CF的长.

答案：

(1)证明:
∵CD平分$∠ACB$,
∴$∠ACF=∠DCB$,
∵$∠CAF=∠CDB$,
∴$△ACF∽△DCB$.
(2)证明:如图,连接AD,过D作$DH⊥CA$,交CA的延长线于点H,作$DG⊥CB$于G,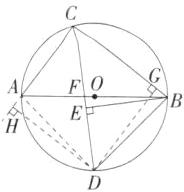
∵AB是$⊙O$的直径,
∴$∠ACB=90°,∠ADB=90°$,
∴四边形CHDG是矩形,
∴$∠HDG=90°$,
∴$∠ADH=∠BDG=90° - ∠ADG$,
∵CD平分$∠ACB$,
∴$∠ACD=∠GCD,DH=DG$,
∴$AD=BD,△ADH≌△BDG$,矩形CHDG是正方形,
∴$AH=BG,CH=CG$,
∴$AC + BC=CH + CG$,在正方形CHDG中,$∠CHD=90°,CH=DH$,
∴$CH + DH=\sqrt{2}CD$,即$AC + BC=\sqrt{2}CD$.
(3)
∵$AC=3,BC=4$,且$AC + BC=\sqrt{2}CD$,
∴$3 + 4=\sqrt{2}CD$,
∴$CD=\frac{7\sqrt{2}}{2}$,
∵$△ACF∽△DCB$,
∴$\frac{CF}{BC}=\frac{AC}{CD}$,
∴$CF=\frac{AC·BC}{CD}=\frac{3×4}{\frac{7\sqrt{2}}{2}}=\frac{12\sqrt{2}}{7}$.