第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
23.「2025江苏南京金陵中学仙林分校月考」(8分)某超市于今年年初以每件25元的价格购进一批商品.当商品售价为40元/件时,一月份销售256件.二、三月该商品十分畅销,销售量持续走高.在售价不变的基础上,三月份的销售量达到400件.设二、三这两个月的月平均增长率不变.
(1)求二、三这两个月的月平均增长率.
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,销售单价与月平均销量的关系如表:
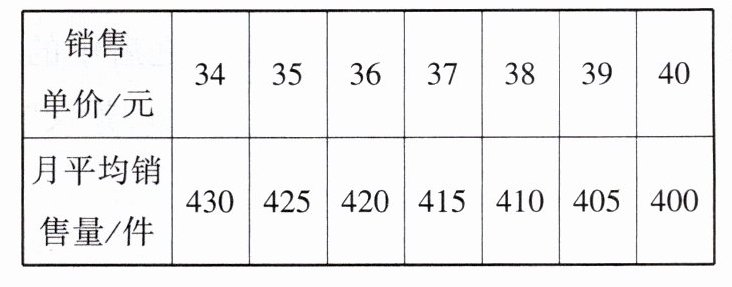
若要使利润达到4250元,且尽可能多地提升月平均销售量,则销售单价应定为多少元?
(1)求二、三这两个月的月平均增长率.
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,销售单价与月平均销量的关系如表:

若要使利润达到4250元,且尽可能多地提升月平均销售量,则销售单价应定为多少元?
答案:
解析
(1)二、三这两个月的月平均增长率为x,根据题意可得$256(1 + x)^2 = 400$, (2分)解得$x_1 = \frac{1}{4} = 25\%$,$x_2 = -\frac{9}{4}$(不合题意,舍去)。 (3分)答:二、三这两个月的月平均增长率为25%。 (4分)
(2)由表知,该商品每降价1元,销售量增加5件。设当每件该商品降价m元时,商品获利4250元,根据题意可得$(40 - 25 - m)(400 + 5m) = 4250$, (6分)解得$m_1 = 5$,$m_2 = -70$(不合题意,舍去)。 (7分)答:当每件该商品降价5元时,商场获利4250元。 (8分)
(1)二、三这两个月的月平均增长率为x,根据题意可得$256(1 + x)^2 = 400$, (2分)解得$x_1 = \frac{1}{4} = 25\%$,$x_2 = -\frac{9}{4}$(不合题意,舍去)。 (3分)答:二、三这两个月的月平均增长率为25%。 (4分)
(2)由表知,该商品每降价1元,销售量增加5件。设当每件该商品降价m元时,商品获利4250元,根据题意可得$(40 - 25 - m)(400 + 5m) = 4250$, (6分)解得$m_1 = 5$,$m_2 = -70$(不合题意,舍去)。 (7分)答:当每件该商品降价5元时,商场获利4250元。 (8分)
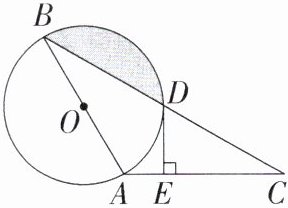
24.「2023山东东营中考改编」(8分)如图,在$\triangle ABC$中,$AB= AC$,以AB为直径的$\odot O$交BC于点D,$DE⊥AC$,垂足为E.
(1)求证:DE是$\odot O$的切线.
(2)若$∠C= 30^{\circ },CD= 2\sqrt {3}$,求$\widehat {BD}$的长和图中阴影部分的面积.
(1)求证:DE是$\odot O$的切线.
(2)若$∠C= 30^{\circ },CD= 2\sqrt {3}$,求$\widehat {BD}$的长和图中阴影部分的面积.

答案:
解析
(1)证明:如图,连接OD,则$OD = OB$,
∴$\angle ODB = \angle B$。
∵$AB = AC$,
∴$\angle C = \angle B$,
∴$\angle ODB = \angle C$,
∴$OD// AC$, (1分)
∵$DE\perp AC$,
∴$\angle ODE = \angle CED = 90^{\circ}$, (2分)
∵OD是$\odot O$的半径,
∴DE是$\odot O$的切线。 (3分)
(2)如图,连接AD,
∵AB是$\odot O$的直径,
∴$\angle ADB = 90^{\circ}$,
∴$AD\perp BC$,
∵$AB = AC$,$CD = 2\sqrt{3}$,
∴$BD = CD = 2\sqrt{3}$, (4分)
∵$\angle B = \angle C = 30^{\circ}$,
∴$AB = 2AD$,在$Rt\triangle ABD$中,$BD^2 + AD^2 = AB^2$,
∴$BD^2 + AD^2 = (2AD)^2$,解得$AD = 2$(舍负), (5分)
∵$OD = OA$,$\angle AOD = 2\angle B = 60^{\circ}$,
∴$\triangle AOD$是等边三角形,$\angle BOD = 120^{\circ}$,
∴$OD = AD = 2$, (6分)
∴$\widehat{BD}$的长=$\frac{120\pi×2}{180} = \frac{4\pi}{3}$, (7分)图中阴影部分的面积=$\frac{120×\pi×2^2}{360} - \frac{1}{2}×2\sqrt{3}×2×\frac{1}{2} = \frac{4\pi}{3} - \sqrt{3}$。 (8分)
(1)证明:如图,连接OD,则$OD = OB$,
∴$\angle ODB = \angle B$。
∵$AB = AC$,
∴$\angle C = \angle B$,
∴$\angle ODB = \angle C$,
∴$OD// AC$, (1分)
∵$DE\perp AC$,
∴$\angle ODE = \angle CED = 90^{\circ}$, (2分)
∵OD是$\odot O$的半径,
∴DE是$\odot O$的切线。 (3分)
(2)如图,连接AD,
∵AB是$\odot O$的直径,
∴$\angle ADB = 90^{\circ}$,
∴$AD\perp BC$,
∵$AB = AC$,$CD = 2\sqrt{3}$,
∴$BD = CD = 2\sqrt{3}$, (4分)
∵$\angle B = \angle C = 30^{\circ}$,
∴$AB = 2AD$,在$Rt\triangle ABD$中,$BD^2 + AD^2 = AB^2$,
∴$BD^2 + AD^2 = (2AD)^2$,解得$AD = 2$(舍负), (5分)
∵$OD = OA$,$\angle AOD = 2\angle B = 60^{\circ}$,
∴$\triangle AOD$是等边三角形,$\angle BOD = 120^{\circ}$,
∴$OD = AD = 2$, (6分)
∴$\widehat{BD}$的长=$\frac{120\pi×2}{180} = \frac{4\pi}{3}$, (7分)图中阴影部分的面积=$\frac{120×\pi×2^2}{360} - \frac{1}{2}×2\sqrt{3}×2×\frac{1}{2} = \frac{4\pi}{3} - \sqrt{3}$。 (8分)
查看更多完整答案,请扫码查看


