《2025年5年中考3年模拟九年级数学全一册苏科版》

1.「2025江苏无锡外国语学校期中」如果两个相似三角形的面积比为$1:2$,那么它们的对应角平分线的比为 (D)
A.$1:4$
B.$1:2$
C.$1:16$
D.$1:\sqrt {2}$

答案： 1.D
∵两个相似三角形的面积比为1:2,
∴这两个相似三角形的相似比为$1:\sqrt{2}$,
∴它们的对应角平分线的比为$1:\sqrt{2}$.故选D.

2. 如图,D、E分别是AC、AB上的点,且$∠CDE+$$∠B= 180^{\circ }$,F、G分别是DE、BC的中点.若AD$=3,AB= 5,AG= 4$,则AF的长为 (A)
A.$\frac {12}{5}$
B.$\frac {3}{4}$
C.$\frac {16}{9}$
D.$\frac {15}{4}$

答案： 2.A
∵∠CDE+∠B=180°,∠ADE+∠CDE=180°,
∴∠ADE=∠B,
∵∠EAD=∠CAB,
∴△EAD∽△CAB,
∴$\frac{AD}{AB}=\frac{AF}{AG}$,
∵$\frac{3}{5}=\frac{AF}{4}$,
∴$AF=\frac{12}{5}$.故选A.

3.新尺规作图 求证:相似三角形对应边上的中线之比等于相似比.
要求:
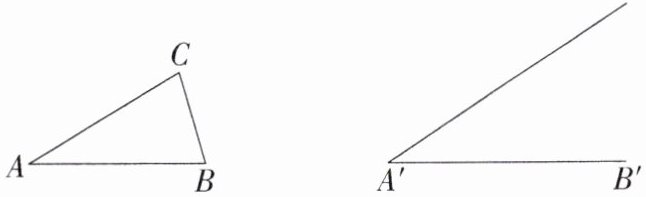
(1)根据给出的$\triangle ABC及线段A'B',∠A'(∠A'$$=∠A)$,以线段$A'B'$为一边,在给出的图形上用尺规作出$\triangle A'B'C'$,使得$\triangle A'B'C'\backsim$$\triangle ABC$,不写作法,保留作图痕迹.
(2)在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

答案：
3.解析　
(1)如图所示,△A'B'C'即为所求.
　　　 　　　　　
(2)已知:如图,△ABC∽△A'B'C',$\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k$,D是AB的中点,D'是A'B'的中点.求证:$\frac{C'D'}{CD}=k$.
　　　　　
证明:
∵D是AB的中点,D'是A'B'的中点,
∴$AD=\frac{1}{2}AB$,$A'D'=\frac{1}{2}A'B'$,
∴$\frac{A'D'}{AD}=\frac{\frac{1}{2}A'B'}{\frac{1}{2}AB}=\frac{A'B'}{AB}$,
∵△ABC∽△A'B'C',
∴$\frac{A'B'}{AB}=\frac{A'C'}{AC}$,∠A'=∠A,
∵$\frac{A'D'}{AD}=\frac{A'C'}{AC}$,∠A'=∠A,
∴△A'C'D'∽△ACD,
∴$\frac{C'D'}{CD}=\frac{A'C'}{AC}=k$.

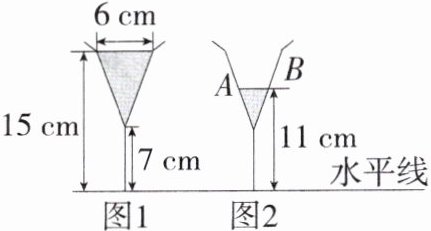
4.「2024江苏盐城亭湖一模,」图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面$AB= $____.

答案：
4.答案　3cm
解析　如图,过O作OM⊥CD,垂足为M,过O'作O'N⊥AB,垂足为N,
　　　　　　
∵CD//AB,
∴△CDO∽△ABO',
∴$\frac{CD}{AB}=\frac{OM}{O'N}$,
∵OM=15 - 7=8(cm),O'N=11 - 7=4(cm),
∴$\frac{6}{AB}=\frac{8}{4}$,
∴AB=3cm.

5.「2024广西南宁段考,」如图,$\triangle ABC$是一块锐角三角形余料,边$BC= 120mm$,高$AD= 80mm$,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,设该矩形的长$QM= y mm$,宽$MN= x mm.$
(1)求证:$y= 120-\frac {3}{2}x.$
(2)当x与y分别取什么值时,矩形PQMN的面积最大？最大面积是多少？

答案： 5.解析　
(1)证明:
∵四边形PQMN是矩形,
∴PN//BC,
∴△APN∽△ABC,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
∵AD=80mm,QM=PN=y mm,MN=ED=x mm,
∴AE=(80 - x)mm,
∴$\frac{y}{120}=\frac{80 - x}{80}$,
∴$y=120-\frac{3}{2}x$.
(2)设矩形PQMN的面积为S mm²,则$S=xy=x\left(120-\frac{3}{2}x\right)=-\frac{3}{2}x^{2}+120x=-\frac{3}{2}(x - 40)^{2}+2400$,
∴当x = 40时,y = 60,此时矩形的面积最大,最大面积为2400 mm².