《2025年5年中考3年模拟九年级数学全一册苏科版》

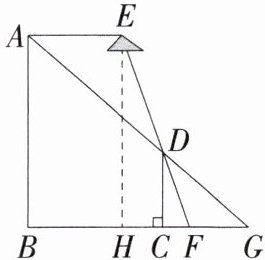
7.「2025江苏无锡惠山金桥双语实验学校月考」小明利用数学课所学知识测量学校门口路灯的高度.如图,$AB$为路灯主杆,$AE$为路灯的悬臂,$CD是长为1.8$米的标杆.已知路灯悬臂$AE与地面BG$平行,当标杆竖立于地面时,主杆顶端$A$、标杆顶端$D和地面上一点G$在同一直线上,此时小明发现路灯$E$、标杆顶端$D和地面上另一点F$也在同一条直线上(路灯主杆底端$B$、标杆底端$C和地面上点F$、点$G$在同一水平线上).这时小明测得$FG长1.5$米,路灯的正下方$H距离路灯主杆底端B的距离为3$米.请根据以上信息,求出路灯主杆$AB$的高度.

答案： 如图,过点D作DM⊥AB于M,交EH于点N,
∵AE//BG,AB⊥BG,
∴AE⊥AB,
∵DM⊥AB,
∴AE//MD//BG,
∴AM等于△ADE的边AE上的高,
∵AB⊥BG,EH⊥BG,CD⊥BG,
∴AB//EH//CD,
∴AE=BH=3米,BM=CD=1.8米,
∵AE//BG,
∴$\frac{AE}{GF}=\frac{AM}{CD}$,即$\frac{3}{1.5}=\frac{AM}{1.8}$,
∴AM=3.6米,
∴AB=AM+BM=5.4米.答:路灯主杆AB的高度为5.4米.

8.「2024河南天宏联考三模」集装箱作为国际贸易中最主要的运输工具之一,因其方便快捷、安全可靠等特点被广泛应用于全球货运领域,而集装箱搬运车则是为了更方便、更高效地对集装箱进行运输、搬运和堆放而设计的机械设备.如图所示的是该集装箱搬运车的简化示意图,测得$CE= 3m$,矩形$DEFG$为底盘,底盘的长和宽分别为$4m和0.9m$,$BG= 2m$,$AB\perp BF$,$DC\perp AE$,点$B$、$G$、$F$在同一水平面上,求集装箱顶部到地面的高度$AB$.(结果精确到$0.1m$,参考数据：$\sqrt{7}\approx 2.65$)

答案： 如图,延长AE交BF于H;
∵AB⊥BF,DC⊥AE,
∴∠B=∠DCE=90°,
∵四边形DEFG是矩形,
∴∠EFH=90°,DE//BH,
∴∠EFH=∠DCE,∠H=∠DEC,
∴△EFH∽△DCE,
∴$\frac{FH}{CE}=\frac{EH}{DE}$,
∴$\frac{FH}{3}=\frac{EH}{4}$,
∴FH=$\frac{3}{4}$EH,在Rt△EFH中,EF=0.9m,EF²+FH²=EH²,
∴0.9² + $(\frac{3}{4}EH)$² = EH²,
∴EH=$\frac{18\sqrt{7}}{35}$m,
∴FH=$\frac{27\sqrt{7}}{70}$≈1.02(m),
∴BH=BG+GF+FH=2 + 4 + 1.02 = 7.02(m).
∵AB⊥BF,EF⊥BH,
∴EF//AB,
∴△EFH∽△ABH,
∴$\frac{EF}{AB}=\frac{FH}{BH}$,
∴$\frac{0.9}{AB}=\frac{1.02}{7.02}$,
∴AB≈6.2m.答:集装箱顶部到地面的高度AB约为6.2m.