第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 学科多解法「2024 江苏盐城滨海期中」已知平面直角坐标系中的三个点分别为 $ A(1,-1) $、$ B(-2,5) $、$ C(4,-6) $,则 $ A $、$ B $、$ C $ 这三个点
可以
确定一个圆(填“可以”或“不可以”)。
答案:
可以
2. 小明不小心把爷爷心爱的紫砂壶摔碎了,他想给爷爷买一套口径一样的茶壶,但是碎片被奶奶打扫走了,只剩了一个碎片,其示意图如图所示,你能确定茶壶的半径吗?如果能,请作出图形。


答案:
能.如图所示,在圆弧上任取三点A、B、C,连接AC,BC,作线段AC的垂直平分线OD和线段BC的垂直平分线OE,两直线交于点O,连接OC,OC的长就是茶壶的半径.

能.如图所示,在圆弧上任取三点A、B、C,连接AC,BC,作线段AC的垂直平分线OD和线段BC的垂直平分线OE,两直线交于点O,连接OC,OC的长就是茶壶的半径.

3. 「2024 江苏无锡滨湖期中」已知 $ \odot O $ 是 $ \triangle ABC $ 的外接圆,那么点 $ O $ 一定是 $ \triangle ABC $ 的(
A.三个顶角的平分线的交点
B.三边上的高的交点
C.三边的中线的交点
D.三边的垂直平分线的交点
D
)A.三个顶角的平分线的交点
B.三边上的高的交点
C.三边的中线的交点
D.三边的垂直平分线的交点
答案:
D
4. 「2025 江苏镇江新区期中」如图,在平面直角坐标系 $ xOy $ 中,点 $ A(0,3) $,点 $ B(2,1) $,点 $ C(2,-3) $,则 $ \triangle ABC $ 的外心坐标应是( )

A.$ (-2,-2) $
B.$ (-2,-1) $
C.$ (-1,-2) $
D.$ (-1,-1) $

A.$ (-2,-2) $
B.$ (-2,-1) $
C.$ (-1,-2) $
D.$ (-1,-1) $
答案:
B 分别作AB与BC的垂直平分线,两垂线的交点$O'$即为$\triangle ABC$的外心,如图,根据坐标可得$O'(-2,-1)$,故选B.

B 分别作AB与BC的垂直平分线,两垂线的交点$O'$即为$\triangle ABC$的外心,如图,根据坐标可得$O'(-2,-1)$,故选B.

5. 「2024 江苏扬州仪征一模」如图,$ O $ 是 $ \triangle ABC $ 的外心,则 $ \angle 1+\angle 2+\angle 3= $____。


答案:
答案 $90^{\circ}$
解析 如图,
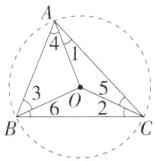
$\because OA=OB,\therefore \angle 3=\angle 4$,同理,$\angle 1=\angle 5$,$\angle 2=\angle 6$,$\because \angle 3+\angle 4+\angle 1+\angle 5+\angle 2+\angle 6=180^{\circ}$,$\therefore \angle 1+\angle 2+\angle 3=90^{\circ}$.
答案 $90^{\circ}$
解析 如图,

$\because OA=OB,\therefore \angle 3=\angle 4$,同理,$\angle 1=\angle 5$,$\angle 2=\angle 6$,$\because \angle 3+\angle 4+\angle 1+\angle 5+\angle 2+\angle 6=180^{\circ}$,$\therefore \angle 1+\angle 2+\angle 3=90^{\circ}$.
6. 易错题「2025 江苏扬州宝应月考」在 $ \text{Rt} \triangle ABC $ 中,$ AC= 3 $,$ BC= 4 $,则它的外接圆的半径为____。
答案:
答案 $\frac{5}{2}$或2
解析 ①如图,当$\angle C=90^{\circ}$时,$\because BC=4$,$AC=3$,

$\therefore AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}}=5$,$\therefore Rt\triangle ABC$外接圆的半径为$\frac{AB}{2}=\frac{5}{2}$;
②如图,当$\angle A=90^{\circ}$时,$\because BC=4$,
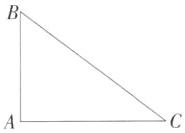
$\therefore Rt\triangle ABC$外接圆的半径为$\frac{BC}{2}=2$.
综上所述,$Rt\triangle ABC$的外接圆的半径为$\frac{5}{2}$或2.
答案 $\frac{5}{2}$或2
解析 ①如图,当$\angle C=90^{\circ}$时,$\because BC=4$,$AC=3$,

$\therefore AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}}=5$,$\therefore Rt\triangle ABC$外接圆的半径为$\frac{AB}{2}=\frac{5}{2}$;
②如图,当$\angle A=90^{\circ}$时,$\because BC=4$,

$\therefore Rt\triangle ABC$外接圆的半径为$\frac{BC}{2}=2$.
综上所述,$Rt\triangle ABC$的外接圆的半径为$\frac{5}{2}$或2.
7. 「2023 江西中考」如图,点 $ A $,$ B $,$ C $,$ D $ 均在直线 $ l $ 上,点 $ P $ 在直线 $ l $ 外,则经过其中任意三个点,最多可画出圆的个数为(
A.3
B.4
C.5
D.6
D
)A.3
B.4
C.5
D.6
答案:
D 根据过不在同一直线上的三点确定一个圆得,经过其中任意三个点,最多可画出圆的个数为6,故选D.
8. 「2025 江苏镇江丹徒期中」如图,$ A $、$ O $ 在网格中小正方形的顶点处,每个小正方形的边长为 1,在此网格中找两个格点(即小正方形的顶点)$ B $、$ C $,使 $ O $ 为 $ \triangle ABC $ 的外心,则 $ BC $ 的长度是( )

A.$ 3\sqrt{2} $
B.$ 2\sqrt{5} $
C.4
D.$ \sqrt{17} $

A.$ 3\sqrt{2} $
B.$ 2\sqrt{5} $
C.4
D.$ \sqrt{17} $
答案:
A $\because$点O为$\triangle ABC$的外心,$\therefore OA=OB=OC$,点B和点C的位置如图所示,$\therefore BC=\sqrt{3^{2}+3^{2}}=3\sqrt{2}$,故选A.

A $\because$点O为$\triangle ABC$的外心,$\therefore OA=OB=OC$,点B和点C的位置如图所示,$\therefore BC=\sqrt{3^{2}+3^{2}}=3\sqrt{2}$,故选A.

9. 「2025 江苏无锡新城中学月考」如图,线段 $ AB= 6 $,$ C $ 为线段 $ AB $ 上的一个动点,以 $ AC $、$ BC $ 为边作等边 $ \triangle ACD $ 和等边 $ \triangle BCE $,$ \odot O $ 外接于 $ \triangle CDE $,则 $ \odot O $ 半径的最小值为( )

A.6
B.$ \sqrt{3} $
C.$ 2\sqrt{3} $
D.3

A.6
B.$ \sqrt{3} $
C.$ 2\sqrt{3} $
D.3
答案:
B 如图,分别作$\angle DAB$与$\angle ABE$的平分线,交点为P.$\because \triangle ACD$和$\triangle BCE$都是等边三角形,

$\therefore AP$垂直平分CD,$BP$垂直平分CE.又$\because$圆心O在CD、CE的垂直平分线上,$\therefore$交点P与圆心O重合,即圆心O是一个定点.连接OC,若半径OC最短,则$OC\perp AB$.$\therefore OA=OB$,$\therefore AC=BC=3$,在$Rt\triangle AOC$中,$\angle OAC=30^{\circ}$,$\therefore OA=2OC$.$\because OA^{2}=OC^{2}+AC^{2}$,$\therefore 3OC^{2}=9$,$\therefore OC=\sqrt{3}$,$\therefore \odot O$半径的最小值为$\sqrt{3}$.故选B.
B 如图,分别作$\angle DAB$与$\angle ABE$的平分线,交点为P.$\because \triangle ACD$和$\triangle BCE$都是等边三角形,

$\therefore AP$垂直平分CD,$BP$垂直平分CE.又$\because$圆心O在CD、CE的垂直平分线上,$\therefore$交点P与圆心O重合,即圆心O是一个定点.连接OC,若半径OC最短,则$OC\perp AB$.$\therefore OA=OB$,$\therefore AC=BC=3$,在$Rt\triangle AOC$中,$\angle OAC=30^{\circ}$,$\therefore OA=2OC$.$\because OA^{2}=OC^{2}+AC^{2}$,$\therefore 3OC^{2}=9$,$\therefore OC=\sqrt{3}$,$\therefore \odot O$半径的最小值为$\sqrt{3}$.故选B.
10. 「2024 江苏宿迁沭阳如东实验学校月考」如图,在 $ \triangle ABC $ 中,$ AB= AC= 2\sqrt{10} $,$ BC= 4 $,$ \odot O $ 是 $ \triangle ABC $ 的外接圆,则 $ \odot O $ 的半径为____。
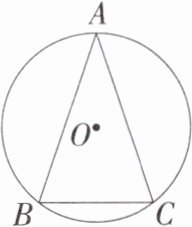
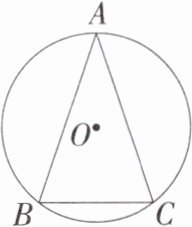
答案:
答案 $\frac{10}{3}$
解析 如图,过点A作$AD\perp BC$,垂足为D,连接OB、OC,
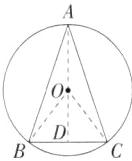
$\because AB=AC$,$AD\perp BC$,$\therefore AD$垂直平分BC,$\because OB=OC$,$\therefore$点O在BC 的垂直平分线上,即O在AD上,$\because BC=4$,$\therefore BD=\frac{1}{2}BC=2$,在$Rt\triangle ABD$中,$\angle ADB=90^{\circ}$,$AB=2\sqrt{10}$,$\therefore AD=\sqrt{AB^{2}-BD^{2}}=6$,设$OA=OB=r$,则$OD=6-r$.在$Rt\triangle OBD$中,$\angle ODB=90^{\circ}$,$\therefore OD^{2}+BD^{2}=OB^{2}$,即$(6-r)^{2}+2^{2}=r^{2}$,解得$r=\frac{10}{3}$,即$\odot O$ 的半径为$\frac{10}{3}$.
答案 $\frac{10}{3}$
解析 如图,过点A作$AD\perp BC$,垂足为D,连接OB、OC,

$\because AB=AC$,$AD\perp BC$,$\therefore AD$垂直平分BC,$\because OB=OC$,$\therefore$点O在BC 的垂直平分线上,即O在AD上,$\because BC=4$,$\therefore BD=\frac{1}{2}BC=2$,在$Rt\triangle ABD$中,$\angle ADB=90^{\circ}$,$AB=2\sqrt{10}$,$\therefore AD=\sqrt{AB^{2}-BD^{2}}=6$,设$OA=OB=r$,则$OD=6-r$.在$Rt\triangle OBD$中,$\angle ODB=90^{\circ}$,$\therefore OD^{2}+BD^{2}=OB^{2}$,即$(6-r)^{2}+2^{2}=r^{2}$,解得$r=\frac{10}{3}$,即$\odot O$ 的半径为$\frac{10}{3}$.
查看更多完整答案,请扫码查看


