《2025年5年中考3年模拟九年级数学全一册苏科版》

1. 在四张完全相同的卡片上分别写上$-\frac {1}{2},0,1,2$四个数,然后放入一个不透明的袋子中摇匀,现从中随机抽取第一张卡片记下数为$a$,放回摇匀,然后随机抽取第二张卡片记下数为$b$,且$a + b = m$,则$m的值使关于x的一元二次方程(m-\frac {3}{2})x^{2}+2x+1= 0$有实数解的概率是____$\frac{11}{16}$。

答案： 答案　$\frac{11}{16}$
　解析
∵关于x的一元二次方程$(m - \frac{3}{2})x² + 2x + 1 = 0$有实数解，
∴$b² - 4ac ≥ 0$，且$m - \frac{3}{2} ≠ 0$，即$4 - 4(m - \frac{3}{2})×1 ≥ 0$，且$m - \frac{3}{2} ≠ 0$，
∴$m ≤ \frac{5}{2}$且$m ≠ \frac{3}{2}$。
　列表如下:
　　$\frac{1}{2}$　　0　　　1　　　2
　　　　−$\frac{1}{2}$　　　　−1　　−$\frac{1}{2}$　　$\frac{1}{2}$　　$\frac{3}{2}$
　　　　　0　　　　　$\frac{1}{2}$　　0　　　1　　　2
　　　　　1　　　　　$\frac{1}{2}$　　　1　　　2　　　3
　　　　　2　　　　　$\frac{3}{2}$　　　2　　　3　　　4
　由表格可知，共有16种等可能的结果，其中满足$m ≤ \frac{5}{2}$且$m ≠ \frac{3}{2}$的有11种，
∴m的值使关于x的一元二次方程$(m - \frac{3}{2})x² + 2x + 1 = 0$有实数解的概率为$\frac{11}{16}$。

2. 有四张正面分别标有数$-1$、$0$、$2$、$3$的不透明卡片,它们除了数不同外其余全部相同。现将它们背面朝上,洗匀后从中随机抽取一张,将该卡片上的数记为$a$,则关于$x的不等式组\left\{\begin{array}{l} \frac {3x-2}{2}\lt x+1,\\ ax＞8\end{array} \right. $有解的概率为$\frac{1}{2}$。

答案： 答案　$\frac{1}{2}$
　解析　$\begin{cases}\frac{3x - 2}{2} ＜ x + 1①\\ax ＞ 8②\end{cases}$，解①得$x ＜ 4$。
　当$a = -1$时，不等式组的解集为$x ＜ -8$；
　当$a = 3$时，不等式组的解集为$\frac{8}{3} ＜ x ＜ 4$；
　当$a = 0$或$a = 2$时，不等式组无解。
∴所求概率为$\frac{2}{4} = \frac{1}{2}$。

3. 有 5 张正面分别写有数$-3$、$-1$、$2$、$3$、$4$的卡片,5 张卡片除了数不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数为$a$,抽取后不放回,再从中抽取一张,记卡片上的数为$b$,则抽取的数$a$、$b能使一次函数y = ax + b$的图像经过第一、二、三象限的概率为____。

答案：
答案　$\frac{3}{10}$
　　解析　画树状图如图所示:
　　 由树状图可知共有20种等可能的结果，其中抽取的数a、b能使一次函数$y = ax + b$的图像经过第一、二、三象限的有6种，分别为$a = 2$，$b = 3$；$a = 2$，$b = 4$；$a = 3$，$b = 2$；$a = 3$，$b = 4$；$a = 4$，$b = 2$；$a = 4$，$b = 3$。
∴符合条件的概率为$\frac{6}{20} = \frac{3}{10}$。

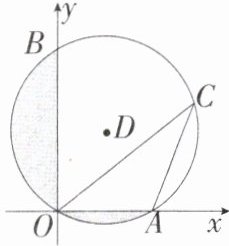
4. 「2024 四川成都青白江二模」如图,在平面直角坐标系中,已知$\odot D经过原点O$,与$x$轴,$y轴分别交于A$,$B$两点,点$B的坐标为(0,2\sqrt {3})$,点$C为\odot D$上的一点,已知$∠OCA = 30^{\circ }$。现假设可以随意在$\odot D$中取点,则这个点取在阴影部分的概率是____。

答案：
答案　$\frac{π - \sqrt{3}}{2π}$
　　解析　连接AB，
　　　　　　　　
∵$∠AOB = 90°$，
∴AB是直径。
∵$∠C = 30°$，
∴$∠OBA = 30°$，
∴$AB = 2OA$。
∵$OB = 2\sqrt{3}$，
∴$(2\sqrt{3})² + OA² = (2OA)²$，
∴$OA = 2$。
∴$S_{阴影}=S_{半圆}-S_{△ABO}=\frac{π×2²}{2}-\frac{1}{2}×2×2\sqrt{3}=2π - 2\sqrt{3}$，$\odot D$的面积$ = 4π$。
∴这个点取在阴影部分的概率是$\frac{2π - 2\sqrt{3}}{4π} = \frac{π - \sqrt{3}}{2π}$。

5. 「2024 甘肃甘南中考」某校组织学生观看“天宫课堂”第二课直播,跟着空间站的翟志刚、王亚平、叶光富三位宇航员学习科学知识,他们相互配合,生动演示了四个实验：(A)微重力环境下的太空“冰雪”实验,(B)液桥演示实验,(C)水油分离实验,(D)太空抛物实验。观看完后,该校对部分学生对四个实验的喜爱情况做了抽样调查,并将调查情况制成了如下不完整的条形统计图和扇形统计图。
请根据图中信息,回答下列问题：
(1)共调查了____名学生,图 2 中 A 所对应扇形的圆心角度数为____。
(2)请补全条形统计图。
(3)若从两名男生、两名女生中随机抽取 2 人参加学校组织的“我爱科学”演讲比赛,请用列表或画树状图的方法,求抽到的学生恰好是一男一女的概率。

答案：

(1)50；$144°$
(2)喜欢D的人数为$50×10\% = 5$，
∴喜欢C的人数为$50 - 20 - 10 - 5 = 15$，补全条形统计图如下:
　　　　　　　
(3)画树状图如下:
　　　
由树状图可知，共有12种等可能的结果，其中抽到的学生恰好是一男一女的结果有8种，
∴抽到的学生恰好是一男一女的概率为$\frac{8}{12} = \frac{2}{3}$。