《2025年5年中考3年模拟九年级数学全一册苏科版》

11.「2024浙江嘉兴桐乡六中教育集团月考」若实数a为不大于6的非负整数,则使关于x的分式方程$\frac {1}{x-3}+\frac {x-a}{3-x}= 1$的解为整数的概率为$\frac{3}{7}$.

答案： $\frac{3}{7}$

12.新考向 地域文化「2024江苏淮安中考」(12分)历史文化名城淮安有着丰富的旅游资源.小明计划假期来淮安游玩,他打算从3个人文景点(A.周恩来纪念馆;B.吴承恩故居;C.河下古镇)中随机选取一个,再从2个自然景点(D.金湖水上森林;E.铁山寺国家森林公园)中随机选取一个.
(1)小明从人文景点中选中河下古镇的概率是____.
(2)用画树状图或列表的方法求小明恰好选中周恩来纪念馆和铁山寺国家森林公园的概率.

答案：

(1)$\frac{1}{3}$。
(2)画树状图如图所示： 由树状图可知，共有6种等可能的结果，其中小明恰好选中周恩来纪念馆和铁山寺国家森林公园的有1种，
∴小明恰好选中周恩来纪念馆和铁山寺国家森林公园的概率为$\frac{1}{6}$。

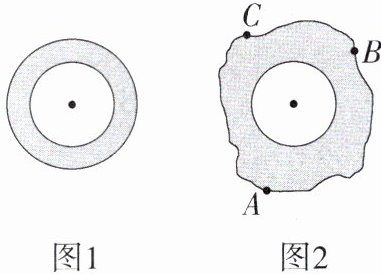
13.(12分)小红和小明在操场上做游戏,他们先在地上画了半径分别为2m和3m的同心圆,如图1,蒙上眼睛在一定距离外向圆内掷小石子,落在阴影内小红胜,落在小圆内小明胜.
(1)你认为这个游戏公平吗? 为什么?
(2)游戏结束,小明边走边想,“反过来,能否按用频率估计概率的方法,来估算不规则图形的面积呢?”他发现地上有一个不规则的封闭图形ABC(如图2),为了知道它的面积,小明在封闭图形内画了一个半径为1m的圆,在不远处向图形内掷石子,且记录如下:
| 掷石子次数 | 50 | 150 | 300 |
| 石子落在小圆内的次数m | 14 | 43 | 93 |
| 石子落在阴影内的次数n | 19 | 85 | 186 |
你能否帮小明求出封闭图形ABC的面积? 试试看.
\

答案：
(1)这个游戏不公平。理由如下：$S_{小圆}=\pi×2^2 = 4\pi(m^2)$，$S_{阴影}=\pi×3^2 - \pi×2^2 = 5\pi(m^2)$，因为$S_{阴影}\neq S_{小圆}$，所以这个游戏不公平。
(2)由题表得出$m$与$n$的比约为$1:2$，所以小圆的面积与封闭图形$ABC$的面积之比约为$1:3$，因为小圆的面积为$\pi×1^2 = \pi(m^2)$，所以封闭图形$ABC$的面积约为$3\pi\ m^2$。

14.(14分)有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数0,1,2;乙袋中装有3个完全相同的小球,分别标有数-1,-2,0.先从甲袋中随机抽取一个小球,记录标有的数为x,再从乙袋中随机抽取一个小球,记录标有的数为y,确定点M的坐标为$(x,y)$.
(1)用画树状图法或列表法列举点M所有可能的坐标.
(2)求点$M(x,y)在函数y= -x+1$的图像上的概率.
(3)在平面直角坐标系xOy中,$\odot O$的半径是2,求过点$M(x,y)能作\odot O$的切线的概率.

答案：

(1)画树状图如下： 由树状图可知，共有9种等可能的结果，点$M$所有可能的坐标为$(0,-1)$，$(0,-2)$，$(0,0)$，$(1,-1)$，$(1,-2)$，$(1,0)$，$(2,-1)$，$(2,-2)$，$(2,0)$。
(2)在直线$y = -x + 1$上的点有$(1,0)$，$(2,-1)$，所以点$M(x,y)$在函数$y = -x + 1$的图像上的概率为$\frac{2}{9}$。
(3)在$\odot O$上的点有$(0,-2)$，$(2,0)$，在$\odot O$外的点有$(1,-2)$，$(2,-1)$，$(2,-2)$，过这5个点均能作$\odot O$的切线，所以过点$M(x,y)$能作$\odot O$的切线的概率为$\frac{5}{9}$。