《2025年5年中考3年模拟九年级数学全一册苏科版》

1.「2025江苏南京联合体期中」已知$\odot O$的半径为3cm,圆心O到直线l的距离为2cm,则l与$\odot O$的交点个数为(C)
A.0
B.1
C.2
D.3

答案： C
∵⊙O的半径为3cm,圆心O到直线l的距离为2cm,且2cm＜3cm,
∴直线l与⊙O相交，有两个交点，故选C.

2.「2023江苏宿迁中考」在同一平面内,已知$\odot O$的半径为2,圆心O到直线l的距离为3,点P为圆上的一个动点,则点P到直线l的最大距离是( )

A.2
B.5
C.6
D.8

答案：
B　如图,
　　　　　　　　
　由题意得,OA=2,OB=3,延长BO与⊙O交于点P,此时点P到直线l的距离最大,最大距离是3+2=5,故选B.

3.「2025江苏盐城阜宁期中」已知$\odot O的半径是一元二次方程x^{2}-2x-3= 0$的一个根,圆心O到直线l的距离$d= 2$,则直线l与$\odot O$的位置关系是(B)
A.相切
B.相交
C.相离
D.平行

答案： B
∵x²−2x−3=0,
∴(x−3)(x+1)=0,
∴x₁=3,x₂=−1(不符合题意,舍去),
∴⊙O的半径等于3,
∵圆心O到直线l的距离d=2,且2＜3,
∴直线l与⊙O相交,故选B

4.「2025江苏宿迁宿城期中」如图,在平面直角坐标系中,$A(2,5)$,$B(4,5)$,$C(6,3)$,$\odot M$经过A,B,C三点。
(1)点M的坐标是(3,2)。
(2)判断$\odot M$与y轴的位置关系,并说明理由。

(2)⊙M与y轴相交.理由:连接AM,由勾股定理得MA=√(1²+3²)=√10,即⊙M的半径为√10,
∵⊙M的圆心M的坐标为(3,2),
∴点M到y轴的距离为3,
∵3＜√10,
∴⊙M与y轴相交.

答案：
(1)(3,2)　
(2)⊙M与y轴相交.理由:连接AM,由勾股定理得MA=√(1²+3²)=√10,即⊙M的半径为√10,
∵⊙M的圆心M的坐标为(3,2),
∴点M到y轴的距离为3,
∵3＜√10,
∴⊙M与y轴相交.

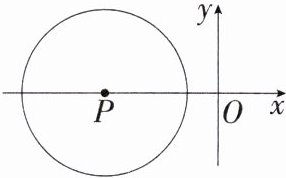
5.学科分类讨特色论思想「2024江苏常州北郊初中月考,☆☆」如图,平面直角坐标系中,半径为2的$\odot P$的圆心P的坐标为$(-3,0)$,将$\odot P$沿x轴向右平移,使$\odot P$与y轴相交,则平移的距离d的取值范围是1＜d＜5。

答案： 1＜d＜5 　解析　当⊙P位于y轴的左侧且与y轴相切时,平移的距离为1;当⊙P位于y轴的右侧且与y轴相切时，平移的距离为5.故⊙P与y轴相交时，平移的距离d 的取值范围是1＜d＜5.

6.学科教材变式特色P73习题13「2025江苏南京鼓楼期中,☆☆」在$Rt\triangle ABC$中,$∠C= 90^{\circ}$,$AC= 5$,$BC= 12$,若以C为圆心,r为半径作的圆与斜边AB有公共点,则r的取值范围为____。

答案：
60/13≤r≤12 　解析　如图,作CD⊥AB于D,
∵∠ACB=90°,AC=5,BC=12,
∴AB=√(AC²+BC²)=13,
　　　　　　　　　　　　　　　　　　
∵1/2CD·AB=1/2BC·AC,
∴CD=60/13.
∴以C为圆心,r为半径作的圆与斜边AB有公共点时,r的取值范围为60/13≤r≤12.

7.学科易错题特色「2024江苏南京秦淮外国语学校月考,☆☆」在平面直角坐标系中,以$P(-3,4)$为圆心,r为半径作圆,当r满足r＞4且r≠5时,圆P与坐标轴有4个交点。

答案： r＞4且r≠5 　解析
∵圆心P的坐标为(−3,4),
∴OP=√(3²+4²)=5,
∴当r=5时，该圆经过原点，这时有三个交点，
∴当r＞4且r≠5时,圆P与坐标轴有4个交点.
易错点 解答此题时要考虑到圆过原点的情况.

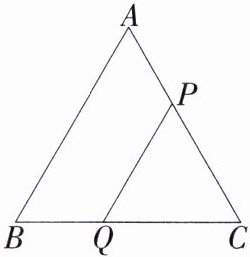
8.「2024江苏无锡锡山期中,☆☆」如图,等边$\triangle ABC$的边长为6cm,点P、点Q分别从点A、点B出发同时向点C以2cm/s的速度移动,到点C时停止。设运动的时间为t s。
(1)几秒时,$\triangle PQC的面积等于\sqrt{3}cm^{2}$？
(2)以Q为圆心,PQ长为半径画圆,当$\odot Q$与线段AB有唯一公共点时,求t的取值范围。

答案：

(1)2秒　
(2)0≤t＜1.5或t=12−6√3 　解析　
(1)由题意得AP=BQ=2tcm,
∵△ABC为等边三角形,
∴AC=BC=6cm,∠C=60°,
∴CQ=PC=(6−2t)cm,
∴△PQC为等边三角形，
∵S△PQC=√3cm²,
∴√3/4(6−2t)²=√3,解得t=2或4.
∵0≤2t≤6,
∴0≤t≤3,
∴t=2.
　答:2秒时,△PQC的面积等于√3cm².
(2)①如图1,当⊙Q与AB相切于点H时,有唯一公共点，连接QH,
∴QH⊥AB,QH=CQ,
∵∠B=60°,
∴∠BQH=30°,
∴BH=1/2BQ=tcm,
∴HQ=√3tcm,
∵CQ=(6−2t)cm,
∴6−2t=√3t,解得t=12−6√3.
②如图2,当⊙Q与线段AB相交，且只有一个交点时，PQ=CQ＞BQ,即6−2t＞2t,
∴t＜1.5,
∴0≤t＜1.5.
　 　　
综上,当⊙Q与线段AB有唯一公共点时,0≤t＜1.5或t=12−6√3.