《2025年5年中考3年模拟九年级数学全一册苏科版》

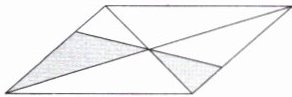
1. [2025 江苏徐州十三中期末]小明把如图所示的平行四边形纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在白色区域的概率是 ( )


A.$\frac{1}{4}$
B.$\frac{3}{4}$
C.$\frac{1}{2}$
D.$\frac{5}{6}$

答案：
如图,根据平行四边形的中心对称性质可得$S_{1}=S_{2}$,且对角线把平行四边形分成四个面积相等的三角形,则白色部分的面积占总面积的$\frac{3}{4}$,所以飞镖落在白色区域的概率为$\frac{3}{4}$,故选B

2. [2023 江苏连云港中考]由 16 个相同的小正方形和 4 个相同的大正方形组成的图形如图所示,在这个图形内任取一点 P,则点 P 落在阴影部分的概率为 (B)
A.$\frac{5}{8}$
B.$\frac{13}{50}$
C.$\frac{13}{32}$
D.$\frac{5}{16}$

答案： 设16个相同的小正方形的边长为a,则4个相同的大正方形的边长为1.5a,
∴点P落在阴影部分的概率为$\frac{2a^{2}+2×(1.5a)^{2}}{16a^{2}+4×(1.5a)^{2}}=\frac{13}{50}$,故选B.

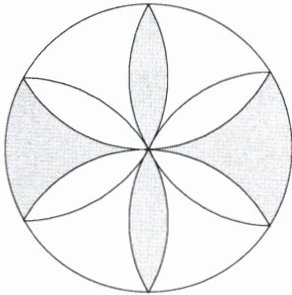
3. 如图所示的图案是用相同半径的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在阴影区域的概率为 ( )


A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{5}$

答案：
如图,根据题意可得$S_{总}=6S_{1}+6S_{2}$,
∴阴影区域的面积= $2S_{1}+2S_{2}=\frac{1}{3}S_{总}$,
∴飞镖落在阴影区域的概率为$\frac{1}{3}$.故选B.

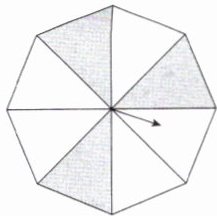
4. [2024 江苏苏州中考]如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是$\frac{3}{8}$.

答案： 答案 $\frac{3}{8}$
解析 根据题意可知,正八边形转盘被分成八个面积相等的三角形,其中阴影部分的面积为3个面积相等的三角形,
∴指针落在阴影部分的概率等于阴影部分的面积除以正八边形的面积,即$\frac{3}{8}$.

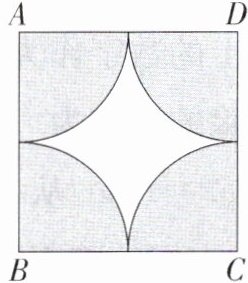
5. [2023 四川攀枝花中考]如图,在正方形 ABCD 中,分别以四个顶点为圆心,以边长的一半为半径画圆弧,若随机向正方形 ABCD 内投一粒米(米粒大小忽略不计),则米粒落在图中阴影部分的概率为______.

$\frac{\pi}{4}$

答案： 答案 $\frac{\pi}{4}$
解析 设正方形的边长为2a,则4个扇形的半径为a,则米粒落在阴影部分的概率为$\frac{\pi a^{2}}{(2a)^{2}}=\frac{\pi}{4}$.

6. 小明与小丽在玩掷沙包的游戏,他们事先在空地上画了直径为 40 cm 和 60 cm 的同心圆,如图,小明在距空地 3 m 开外的地方将沙包随机投掷到该图形内,则沙包落在阴影区域的概率为$\frac{5}{9}$.

答案： 答案 $\frac{5}{9}$
解析 大圆面积:$\pi×\left(\frac{60}{2}\right)^{2}=900\pi(\text{cm}^{2})$,小圆面积:$\pi×\left(\frac{40}{2}\right)^{2}=400\pi(\text{cm}^{2})$,
∴阴影部分面积:$900\pi - 400\pi = 500\pi(\text{cm}^{2})$,
∴沙包落在阴影区域的概率为$\frac{500\pi}{900\pi}=\frac{5}{9}$.

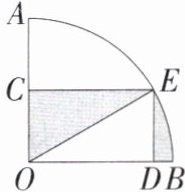
7. [2024 山东威海中考]如图,在扇形 AOB 中,$∠AOB = 90^{\circ}$,点 C 是 AO 的中点.过点 C 作 $CE \perp AO$ 交 $\overset{\frown}{AB}$ 于点 E,过点 E 作 $ED \perp OB$,垂足为点 D.在扇形内随机选取一点 P,则点 P 落在阴影部分的概率是 ( )


A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$

答案：
连接AE,如图,

∵$CE\perp AO$,点C是AO 的中点,
∴$AE=OE$.
∵$OA=OE$,
∴$AE=OE=OA$,
∴$\angle AOE = 60^{\circ}$,
∴$\angle BOE=\angle AOB - \angle COE = 30^{\circ}$,
∵$ED\perp OB$,
∴$\angle ODE = 90^{\circ}$,
∵$\angle COD=\angle OCE = 90^{\circ}$,
∴四边形OCED为矩形,
∴$S_{\triangle OCE}=S_{\triangle ODE}$,
∴阴影部分的面积$=S_{扇形BOE}=\frac{30\pi× OB^{2}}{360}$,
∴点P落在阴影部分 的概率$=\frac{S_{扇形BOE}}{S_{扇形AOB}}=\frac{\frac{30×\pi× OB^{2}}{360}}{\frac{90×\pi× OB^{2}}{360}}=\frac{1}{3}$.故选B.