《2025年5年中考3年模拟九年级数学全一册苏科版》

12.学科易错题正方形ABCD的边长为2,点P在CD边所在直线上,若DP= 1,则tan∠BPC的值是2或$\frac{2}{3}$.

答案： 2或$\frac{2}{3}$

13.「2024江苏常州中考」如图,在矩形ABCD中,对角线BD的垂直平分线分别交边AB、CD于点E、F.若AD= 8,BE= 10,则tan∠ABD= $\frac{1}{2}$.

答案： $\frac{1}{2}$

14.「2024江苏泰州姜堰四校联考」如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为______.

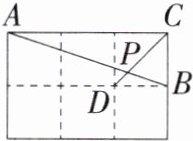
2

答案： 2

15.学科等角转换法「2023浙江湖州中考」如图,标号为①②③④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF,③和④分别是Rt△CDG和Rt△DAH,⑤是正方形EFGH,直角顶点E,F,G,H分别在边BF,CG,DH,AE上.
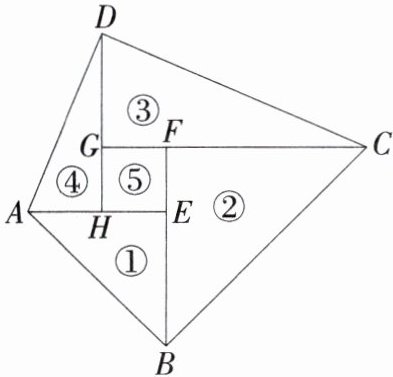
(1)若EF= 3 cm,AE+FC= 11 cm,则BE的长是4cm.
(2)若$\frac{DG}{GH}= \frac{5}{4}$,则tan∠DAH的值是3.

答案：
(1)4　　
(2)3

16.学科设参法「2021广东中考」如图,在Rt△ABC中,∠A= 90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE= AB.
(1)若AE= 1,求△ABD的周长.
(2)若AD= $\frac{1}{3}$BD,求tan∠ABC的值.

答案：
(1)1　
(2)$\sqrt{2}$

17.新课标应用意识「2024河南安阳林州期末」构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图,在Rt△ACB中,∠C= 90°,∠ABC= 30°,延长CB至D,使BD= AB,连接AD,得∠D= 15°,所以tan15°= $\frac{AC}{CD}$= $\frac{1}{2+\sqrt{3}}$= $\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$= 2-$\sqrt{3}$.类比这种方法,计算tan22.5°的值为(B)
A.$\sqrt{2}+1$
B.$\sqrt{2}-1$
C.$\sqrt{2}$
D.$\frac{1}{2}$

答案： B